Processus de mélange en eaux peu profondes
Storyboard 
Les mécanismes de mélange dans les zones peu profondes sont générés par différents types d'ondes. Parmi eux se trouvent les ondes internes, les ondes de surface, l'interaction entre les ondes et les courants, les marées et le déferlement des vagues sur la côte.
ID:(1629, 0)
Mécanismes
Iframe 
Mécanismes
ID:(15614, 0)
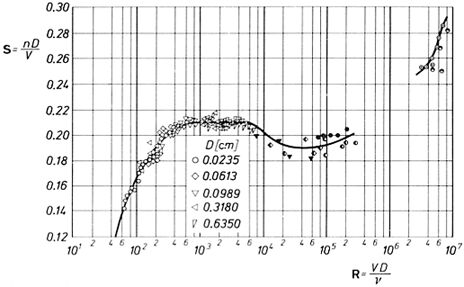
Nombre de Strouhal en fonction du nombre de Reynold
Image 
Le numéro de Strouhal (St) est relié empiriquement à Le le numéro de Reynold (Re). Le numéro de Strouhal (St) est associé à A fréquence de génération de vortex (\omega), a vitesse de friction (U_d), et a profondeur totale (H) est
Cela permet d'estimer, via le le numéro de Reynold (Re), la fréquence à laquelle la concentration peut échanger les composants à diffuser. Cependant, il faut garder à l'esprit que le processus peut être interrompu si la fréquence est inférieure à celle des marées.
ID:(12199, 0)
Contrainte cinématique
Description 
Si l'on suppose qu'il n'y a pas de vent à la surface, on peut supposer qu'il n'y a pas de tension à cet endroit. Par conséquent, il n'y aura de tension de l'eau que sur le fond. Cette tension diminuera linéairement du fond vers la surface. Pour simplifier la modélisation, on peut utiliser la proportion entre a profondeur (z) et a profondeur totale (H), ce qui nous donne un facteur adimensionnel a profondeur relative (\xi). A contrainte cinématique (\tau_x) sera donc proportionnelle à
\tau_x \propto 1-\xi
Étant donné que a contrainte cinématique (\tau_x) est équivalent à la densité d'énergie divisée par la densité, la valeur au fond doit être proportionnelle au carré de la vitesse au fond. Cela est décrit dans le modèle avec a vitesse de friction (U_d) et signifie que
\tau_x \propto U_d^2
Enfin, il y a l'effet de a rugosité (k) du fond marin, c'est-à-dire la proportion de le inégalité (d) et a profondeur totale (H). Cela signifie que a contrainte cinématique (\tau_x) doit être corrigé par un facteur analogue à la profondeur :
\tau_x \propto \displaystyle\frac{1-\xi}{1-k}
Ainsi, un modèle de la forme suivante est obtenu :
| \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi ) |
qui est représenté graphiquement comme suit :
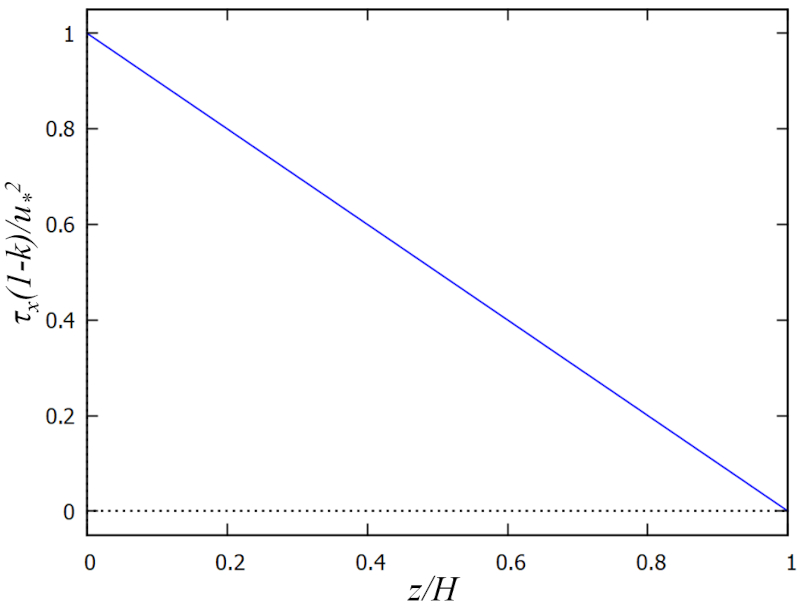
ID:(15630, 0)
Longueur de mélange
Description 
A longueur de mélange (l) correspond à ce qui pourrait être décrit comme la taille des tourbillons. À proximité de la paroi, ces tourbillons ne peuvent avoir qu'une taille maximale égale à la distance par rapport à la paroi, qui est minimale. À mesure que l'on se rapproche de la surface, ils peuvent devenir de plus en plus grands, donc la fonction doit atteindre un maximum à ce point.
Pour simplifier la modélisation, on peut utiliser le rapport entre a profondeur (z) et a profondeur totale (H), ce qui nous donne un facteur sans dimension a profondeur relative (\xi). Ainsi, une fonction simple qui répond à cette description est de la forme :
l \propto \xi\left(1-\displaystyle\frac{1}{2}\xi\right)
D'autre part, le modèle de couche limite de Prandtl montre que ces tourbillons représentent une fraction du flux avec une largeur égale à A profondeur totale (H) et une proportion de a constante de Karman (\kappa), donc :
l \propto \kappa H
Enfin, il faut corriger l'effet de la rugosité de la même manière que pour la contrainte cinématique :
l \propto \displaystyle\frac{\kappa H}{1-k}
Par conséquent, a longueur de mélange (l) peut être modélisé de la manière suivante :
| l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right) |
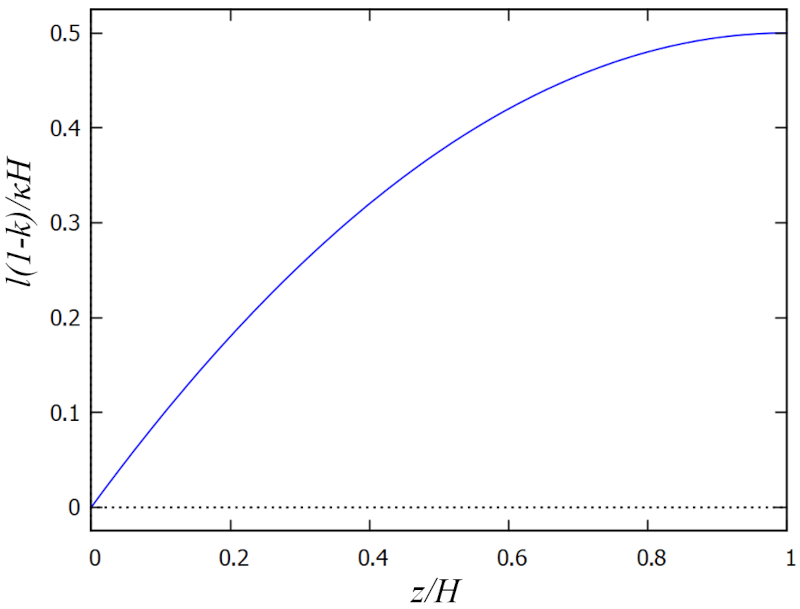
ID:(12201, 0)
Viscosité du tourbillon
Top 
Lorsque Prandtl modélise la formation de tourbillons près des parois, il établit la relation entre a viscosité turbulente (A), a longueur de mélange (l) et le gradient de le profil de vitesse (u_z) en a profondeur (z) de la manière suivante :
| A = l ^2\displaystyle\frac{\partial u_z }{\partial z } |
D'autre part, la force visqueuse typique, qui est modélisée comme la viscosité multipliée par la surface de contact et le gradient de vitesse, correspond dans le cas des turbulences à A contrainte cinématique (\tau_x) :
| \tau_x = A \displaystyle\frac{\partial u_z }{\partial z } |
Des deux équations découle la relation suivante :
| \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 } |
Cette relation permet de calculer a viscosité turbulente (A) en fonction de a contrainte cinématique (\tau_x) et de a longueur de mélange (l), qui sont modélisés dans ce cas. Ainsi, avec a profondeur totale (H), a vitesse de friction (U_d), a rugosité (k), a profondeur relative (\xi) et a constante de Karman (\kappa) :
| A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi } |
qui est représenté ci-dessous :
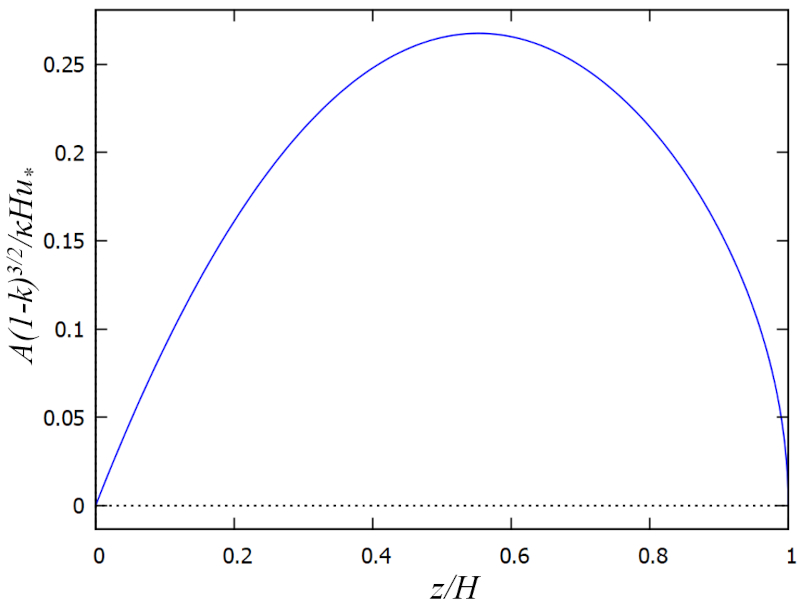
Le résultat est que la viscosité turbulente est maximale à mi-profondeur et se réduit à des valeurs minimales près du fond et près de la surface. En d'autres termes, dans ces zones, le mélange et la perte de quantité de mouvement sont moindres.
ID:(15624, 0)
Profil de vitesse
Top 
Comme a contrainte cinématique (\tau_x) est égal à A viscosité turbulente (A) et au gradient de le profil de vitesse (u_z) en a profondeur (z), l'équation peut être intégrée pour obtenir le profil de vitesse :
u_z = \displaystyle\int_d^z \frac{\tau_x}{A} , dz'
Après avoir intégré cette expression, avec a vitesse de friction (U_d), a constante de Karman (\kappa), a rugosité (k) et a profondeur relative (\xi), on obtient :
| u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right) |
qui correspond à la célèbre loi logarithmique développée par Prandtl et Schlichting.
Le profil est montré dans le graphique suivant :
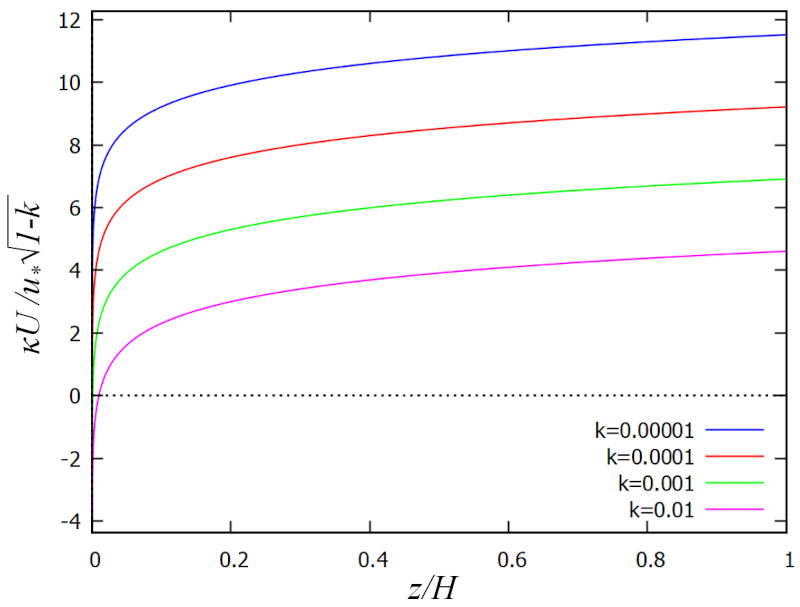
Le profil permet également de relier à la fois ($$) à A vitesse de friction (U_d) en fonction de a rugosité (k) et a constante de Karman (\kappa), ce qui permet à son tour de définir un le traînée inférieure (C_D) avec :
| U ^2 = \displaystyle\frac{ U_d ^2}{ C_D } |
e
| C_D = \displaystyle\frac{ \kappa ^2 }{(1- k ) \ln^2(1/ k )} |
ID:(15623, 0)
Concentration des sédiments
Top 
Si l'on considère le comportement du matériau en suspension, deux facteurs principaux émergent. Tout d'abord, il y a une tendance à la sédimentation avec une vitesse a taux de sédimentation (\omega_s), générant un flux dépendant de ($$), exprimé comme suit :
\omega_s c_z
D'autre part, les tourbillons ont tendance à mélanger l'eau, produisant une diffusion qui transporte les sédiments vers la surface. Ce flux, représenté par a viscosité turbulente (A), est donné par le gradient de ($$) en a profondeur (z), égal à :
A\displaystyle\frac{\partial c_z}{\partial z}
La distribution se forme lorsque les sédiments atteignent l'équilibre, où le flux de sédimentation est égal à la diffusion générée par les tourbillons vers la surface. En intégrant les deux termes de l'équation avec le taux d'érosion (E) et le inégalité (d), nous obtenons la distribution :
c_z=\displaystyle\frac{E}{\omega_s}e^{\displaystyle\int_d^z \omega_s/A dz'}
Après avoir utilisé l'expression obtenue pour a viscosité turbulente (A) avec le facteur de Rouse (R_s), a rugosité (k) et a profondeur relative (\xi), nous obtenons l'expression :
| c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s } |
qui peut être représentée graphiquement comme suit :
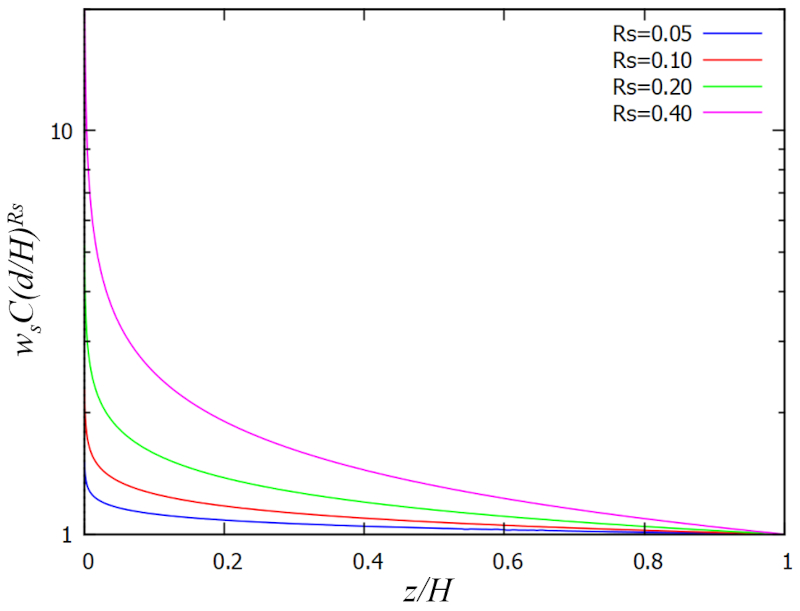
ID:(15631, 0)
Modèle
Top 
Paramètres
Variables
Calculs
Calculs
Calculs
Équations
A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi }
A = kappa * U_d * H * xi * (1- xi /2)*sqrt(1- xi )/(1- k )^(3/2)
A = l ^2\displaystyle\frac{\partial u_z }{\partial z }
A = l ^2*@DIF( u_z , z )
C_D = \displaystyle\frac{ \kappa ^2 }{(1- k ) \ln^2(1/ k )}
C_D = kappa ^2/((1- k )* log(1/ k )^2)
c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s }
c_z =( E / omega_s )*( k / xi )^ R_s
k \equiv \displaystyle\frac{ d }{ H }
k = d / H
l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right)
l = kappa * H * xi *(1 - xi /2)/(1 - k )
R_0 \equiv \displaystyle\frac{ \omega_s }{ \kappa U_d }
R_0 = omega_s /( kappa * U_d )
R_s \equiv R_0 (1 - k )^{3/2}
R_s = R_0 (1 - k )^(3/2)
St \equiv \displaystyle\frac{ \omega H }{ U_d }
St = omega * H / U_d
\tau_x = A \displaystyle\frac{\partial u_z }{\partial z }
tau_x = A *@DIF( u_z , z )
\tau_x = \displaystyle\frac{ A ^2 }{ l ^2 }
tau_x = A ^2 / l ^2
\tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi )
tau_x = U_d ^2 *(1- xi )/(1- k )
U ^2 = \displaystyle\frac{ U_d ^2}{ C_D }
U ^2 = U_d ^2/ C_D
u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right)
u_z = U_d sqrt(1- k )*log( xi / k ))/ kappa
\xi \equiv \displaystyle\frac{ z }{ H }
xi = z / H
ID:(15618, 0)
Le numéro de Strouhal
Équation 
Le numéro de Strouhal (St) caractérise a fréquence de génération de vortex (\omega). Comparez la vitesse associée à A fréquence de génération de vortex (\omega) et sa taille avec celle de l'écoulement représenté par a profondeur totale (H).
Par conséquent, avec cela, nous avons
ID:(12198, 0)
Rugosité du fond
Équation 
Le comportement du courant et des turbulences à générer ou à atténuer dépend de a rugosité (k) du fond marin. Cela est défini en comparant le profil moyen de le inégalité (d) avec le profil de a profondeur totale (H) où il se trouve.
Par conséquent, on définit que a rugosité (k) est
ID:(12183, 0)
Profondeur relative
Équation 
A profondeur relative (\xi) est défini en fonction de a profondeur (z) et a profondeur totale (H), exprimé comme suit :
ID:(12182, 0)
Contrainte cinématique
Équation 
Pour un écoulement laminaire, a force visqueuse (F_v) peut être calculé à partir de les surfaces parallèles (S), a viscosité (\eta), a différence de vitesse entre les surfaces (\Delta v) et a distance entre les surfaces (\Delta z) en utilisant l'équation suivante :
| F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z } |
Dans le cas d'un écoulement turbulent, une analogie peut être établie en définissant une viscosité turbulente (A) comme la viscosité divisée par la densité, associée à la force par surface et à la densité, que nous appellerons a contrainte cinématique (\tau_x), calculé en fonction de le profil de vitesse (u_z) et a profondeur (z) de la manière suivante :
ID:(12191, 0)
La loi de Prandtl
Équation 
En 1925, Prandtl a introduit le concept d'une couche limite où les tourbillons mélangent le fluide et transfèrent le moment de manière similaire à la modélisation du transfert au niveau moléculaire, créant un comportement visqueux. La taille de cette zone est définie comme a longueur de mélange (l) et l'effet est décrit par un analogue à la viscosité correspondant à A viscosité turbulente (A). Ceci peut être estimé avec le gradient de le profil de vitesse (u_z) dans a profondeur (z) en utilisant :
[1] Prandtl, Ludwig (1925). "Bericht über Untersuchungen zur ausgebildeten Turbulenz" (Rapport sur les recherches en turbulence développée). Z. Angew. Math. Mech. 5 (2): 136.
ID:(12186, 0)
Relation de contrainte cinématique
Équation 
A contrainte cinématique (\tau_x) peut être calculé à partir de a viscosité turbulente (A) et a longueur de mélange (l) en utilisant la méthode suivante :
Tout comme a viscosité turbulente (A) est lié à A longueur de mélange (l), le profil de vitesse (u_z) et a profondeur (z) sont définis comme suit :
| A = l ^2\displaystyle\frac{\partial u_z }{\partial z } |
et puisque a contrainte cinématique (\tau_x) est
| \tau_x = A \displaystyle\frac{\partial u_z }{\partial z } |
l'élimination du gradient donne
| \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 } |
ID:(15633, 0)
Diffusivité des vortex océaniques plus profonds
Équation 
A contrainte cinématique (\tau_x) sera maximal près du fond océanique et nul à la surface, à condition qu'il n'y ait pas de vent à la surface de l'océan. Étant associé à A vitesse de friction (U_d) au fond, mais devant être corrigé en raison de l'effet de a rugosité (k), il peut être modélisé en fonction de a profondeur relative (\xi) comme suit :
ID:(12202, 0)
Longueur de mélange
Équation 
La zone de mélange introduite par Prandtl, de taille a longueur de mélange (l), est estimée comme une fraction de l'ordre de a constante de Karman (\kappa) de a profondeur totale (H). De plus, il faut ajuster pour l'effet de a rugosité (k), et prendre en compte que a longueur de mélange (l) dépend de a profondeur relative (\xi), étant nul au fond et approximativement constant et maximal près de la surface. Par conséquent, elle peut être modélisée comme suit :
[1] Prandtl, Ludwig (1925). "Bericht über Untersuchungen zur ausgebildeten Turbulenz" (Rapport sur les recherches en turbulence développée). Z. Angew. Math. Mech. 5 (2): 136.
ID:(12194, 0)
Viscosité du tourbillon
Équation 
À partir de mesures, on peut modéliser a viscosité turbulente (A) en fonction de a profondeur relative (\xi), a profondeur totale (H), a rugosité (k), a vitesse de friction (U_d) et a constante de Karman (\kappa) avec l'expression :
De la même manière que a contrainte cinématique (\tau_x) est lié à A viscosité turbulente (A) et a longueur de mélange (l), il s'ensuit que :
| \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 } |
Si a constante de Karman (\kappa), a profondeur totale (H) et a rugosité (k) sont utilisés :
| l \equiv \displaystyle\frac{ \kappa H }{1 - k } \xi \left(1 - \displaystyle\frac{1}{2} \xi \right) |
et avec a vitesse de friction (U_d) :
| \tau_x \equiv \displaystyle\frac{ U_d ^2}{1- k }(1- \xi ) |
nous obtenons :
| A = \displaystyle\frac{ \kappa H U_d }{(1- k )^{3/2}} \xi \left(1- \displaystyle\frac{1}{2} \xi \right)\sqrt{1- \xi } |
ID:(12185, 0)
Profil de vitesse
Équation 
Le profil de vitesse (u_z) est une fonction de a profondeur relative (\xi) et des paramètres a rugosité (k), a vitesse de friction (U_d) et a constante de Karman (\kappa), représentée de la manière suivante :
Tout comme a contrainte cinématique (\tau_x) se rapporte à A viscosité turbulente (A), le profil de vitesse (u_z) et a profondeur (z), il est défini par
| \tau_x = A \displaystyle\frac{\partial u_z }{\partial z } |
et peut être intégré de le inégalité (d) à A profondeur (z) pour obtenir la vitesse en utilisant l'expression suivante :
u_z=\displaystyle\int_d^z\displaystyle\frac{\tau_x}{A}dz'
Avec la formulation de a viscosité turbulente (A) en termes de a profondeur relative (\xi) ainsi que a profondeur totale (H), a rugosité (k) et a vitesse de friction (U_d), et en considérant que
la formule suivante pour la vitesse est dérivée :
u_z=\displaystyle\frac{U_d\sqrt{1-k}}{\kappa}(\ln(z/d) + \Phi(\xi,k))
où
\Phi=2[\arctan(\lambda)-\arctan(\lambda_0)]-\ln\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)
est défini avec
\lambda=\sqrt{1-\xi}
et
\lambda=\sqrt{1-k}
Étant donné que sur une grande partie de la profondeur
\ln(z/d) \gg \Phi(\xi,k)
le profil de vitesse peut être simplifié à
| u_z = \displaystyle\frac{ U_d }{ \kappa }\sqrt{1-k}\ln\left(\displaystyle\frac{ \xi }{ k }\right) |
ID:(12187, 0)
Coefficient d'amortissement
Équation 
($$) est proportionnel à A vitesse de friction (U_d), avec une constante de proportionnalité qui dépend de a constante de Karman (\kappa) et a rugosité (k), comme suit :
ID:(12184, 0)
Vitesse de surface
Équation 
A vitesse de friction (U_d) est proportionnel à ($$), avec une constante de proportionnalité Le traînée inférieure (C_D), qui représente la relation entre leurs énergies cinétiques respectives :
ID:(12188, 0)
Diffusion d'une concentration de sédiment
Équation 
($$) est une fonction de a profondeur relative (\xi) qui dépend de le taux d'érosion (E), a taux de sédimentation (\omega_s), a rugosité (k) et le facteur de Rouse (R_s), et se calcule de la manière suivante :
Les sédiments ont tendance à se déposer au fond avec une taux de sédimentation (\omega_s), tandis que la diffusion, qui dans ce cas correspond au mélange généré par les tourbillons, induit un flux égal à A viscosité turbulente (A) et au gradient de ($$) en a profondeur (z), de la manière suivante :
A\displaystyle\frac{\partial c_z}{\partial z}+\omega_s c_z= 0
En intégrant cette expression, on obtient :
c_z = \displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/A dz'}
avec a longueur de mélange (l) :
| \tau_x = \displaystyle\frac{ A ^2 }{ l ^2 } |
nous avons :
c_z=\displaystyle\frac{E}{\omega_s}e^{-\displaystyle\int_d^z \omega_s/l\sqrt{\tau_x} dz'}
ce qui donne :
c_z=\displaystyle\frac{E}{\omega_s}\left(\displaystyle\frac{z}{d}\right)^{R_s}\Phi_c(\xi,k)
avec le facteur de Rouse (R_s) et le numéro de réveil (R_0) :
| R_s \equiv R_0 (1 - k )^{3/2} |
où :
\Phi=\left(\displaystyle\frac{1+\lambda}{1+\lambda_0}\right)^{2R_s}e^{2R_s[\arctan(\lambda)-\arctan(\lambda_0)]}
avec :
\lambda=\sqrt{1-\xi}
et :
\lambda=\sqrt{1-k}
Comme sur une grande partie de la profondeur :
\Phi\sim 1
nous obtenons la distribution de concentration :
| c_z = \displaystyle\frac{ E }{ \omega_s }\left(\displaystyle\frac{ k }{ \xi }\right)^{ R_s } |
ID:(12193, 0)
Le numéro de Rouse
Équation 
La valeur le numéro de réveil (R_0) compare la vitesse de sédimentation, qui est en concurrence avec la diffusion associée au courant au fond. Lorsqu'elle est combinée avec a taux de sédimentation (\omega_s), a vitesse de friction (U_d) et a constante de Karman (\kappa), elle donne :
ID:(12195, 0)
Le facteur Rouse
Équation 
La valeur le numéro de réveil (R_0) évalue la vitesse de sédimentation, qui est en concurrence avec la diffusion liée au courant au fond. Combinée avec a taux de sédimentation (\omega_s), a vitesse de friction (U_d) et a constante de Karman (\kappa), elle donne :
| R_0 \equiv \displaystyle\frac{ \omega_s }{ \kappa U_d } |
Dans les cas où le fond marin n'est pas lisse, a rugosité (k) existe et entraîne une correction du nombre de Rouse, que nous appelons le facteur de Rouse :
ID:(15632, 0)
