Storyboard

In the case of greater depths, the energy dissipation mechanisms of vortices are related to viscosity and buoyancy. Which one dominates depends on the situation and can be determined using characteristic numbers associated with both phenomena.

[1] Marine Physics, Jerzy Dera, Elsevier, 1992 (6.2 The Turbulent Exchange of Mass, Heat and Momentum in the Sea)

>Model

ID:(1628, 0)

Iframe

>Top

ID:(15616, 0)

Top

>Top

In general, energy dissipation occurs over the considered time period, so the kinetic energy ($\epsilon_v$) should be compared with a characteristic time ($\tau$) such that

$\displaystyle\frac{d\epsilon}{dt}\sim\displaystyle\frac{\epsilon_v}{\tau}$

There are two types of processes that reduce the energy of vortices until they become thermal fluctuations. On one hand, there's momentum diffusion or viscosity, while on the other hand, there's flotation.

The loss of the kinetic energy ($\epsilon_v$) varies depending on the energy dissipated by viscosity ($\epsilon_{\eta}$) and the energy dissipated by flotation ($\epsilon_{\rho}$) in the characteristic time ($\tau$) as

ID:(15621, 0)

Top

>Top

As the kinetic energy ($\epsilon_v$), where for simplicity we neglect the factor of 1/2 and it depends on the medium density ($\rho$) and the vortex speed ($v_l$),

$\epsilon =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$

the energy loss will be this energy by the characteristic time ($\tau$), which with the mixing length ($l$) is

and thus, the variation is

ID:(15608, 0)

Top

>Top

As the energy dissipated by viscosity ($\epsilon_{\eta}$) is with the viscosity of ocean water ($\eta$), the vortex speed ($v_l$), and the mixing length ($l$),

$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$

the energy loss will be this energy by the characteristic time ($\tau$), which with the mixing length ($l$) is

and thus, the variation is

ID:(15609, 0)

Top

>Top

As the energy dissipated by flotation ($\epsilon_{\rho}$) is with the variación de la densidad ($\Delta\rho$), the aceleración gravitacional ($g$), and the mixing length ($l$):

$\epsilon_{\rho} =\Delta\rho g l$

the energy loss will be this energy by the characteristic time ($\tau$), which is

and thus, the variation is

ID:(15610, 0)

Top

>Top

In the case where diffusive processes are more relevant than flotation ones, it is observed that with the kinetic energy ($\epsilon_v$), the energy dissipated by flotation ($\epsilon_{\rho}$), and the energy dissipated by viscosity ($\epsilon_{\eta}$),

$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$

Given that with the characteristic time ($\tau$), the kinetic energy ($\epsilon_v$) is

and the energy dissipated by viscosity ($\epsilon_{\eta}$) is

the existence of the vortex implies that its kinetic energy is greater than the loss, so with

$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$

it results in the requirement that it must be the case that

ID:(15612, 0)

Top

>Top

In the event that with the kinetic energy ($\epsilon_v$), the energy dissipated by viscosity ($\epsilon_{\eta}$), and the energy dissipated by flotation ($\epsilon_{\rho}$) are such that

$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$

Given that the kinetic energy ($\epsilon_v$) is with the density ($\rho$), the mixing length ($l$), and the vortex speed ($v_l$) in the characteristic time ($\tau$),

and the energy dissipated by flotation ($\epsilon_{\rho}$) is with the variación de la densidad ($\Delta\rho$), the gravitational Acceleration ($g$), and the vortex speed ($v_l$) in the characteristic time ($\tau$),

the existence of the vortex implies that its kinetic energy is greater than the loss, so with

$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$

the requirement arises that with it must be the case that the richardson number ($R_i$) satisfies

ID:(15611, 0)

Description

>Top

The relationship between the reynold's number ($Re$) with the density ($\rho$), the vortex speed ($v_l$), the viscosity of ocean water ($\eta$), and the tamaño característico ($l$) is given by

and the richardson number ($R_i$) with the variación de la densidad ($\Delta\rho$) and the gravitational Acceleration ($g$) is represented by

as shown in the graph below, where both boundary cases mark the stability limit situations:

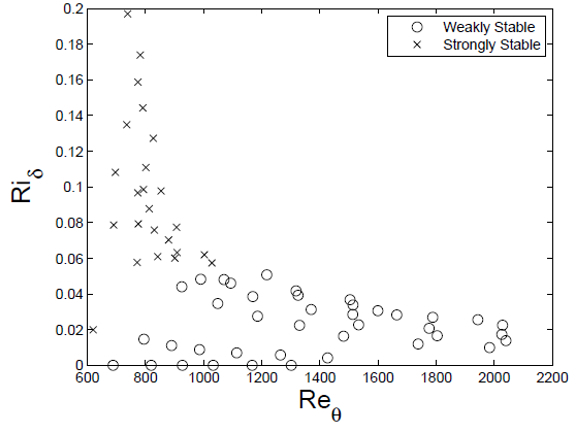
Turbulent Coherent Structures in a Thermally stable Boundary Layer, Owen Williams and Alexander J. Smits, https://www.researchgate.net/publication/228761589_Turbulent_Coherent_Structures_in_a_Thermally_Stable_Boundary_Layer

ID:(12211, 0)

Top

>Top

Parameters

$g$

g

Gravitational Acceleration

m/s^2

$\rho$

rho

Medium density

kg/m^3

$R_i$

R_i

Richardson number

-

$l$

l

Tamaño característico

m

$\Delta\rho$

Drho

Variación de la densidad

kg/m^3

$\eta$

eta

Viscosity of ocean water

Pa s

Variables

$\tau$

tau

Characteristic time

s

$\epsilon_{\rho}$

epsilon_rho

Energy dissipated by flotation

J

$\epsilon_{\eta}$

epsilon_eta

Energy dissipated by viscosity

J

$\epsilon_v$

epsilon_v

Kinetic energy

J

$l$

l

Mixing length

m

$Re$

Re

Reynolds number

-

$v_l$

v_l

Vortex speed

m/s

Calculations

• Alternative method
• Traditional method
• Strategy
• 2D
• 3D

Equation

Number

First, select the equation: to , then, select the variable: to

---

Calculations

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

Variable Given Calculate Target : Equation To be used

Equations

ID:(15620, 0)

Equation

>Top, >Model

There are two types of processes that reduce the energy of vortices until they become thermal fluctuations. On one hand, there's momentum diffusion or viscosity, while on the other hand, there's flotation.

The loss of the kinetic energy ($\epsilon_v$) varies depending on the energy dissipated by viscosity ($\epsilon_{\eta}$) and the energy dissipated by flotation ($\epsilon_{\rho}$) in the characteristic time ($\tau$) as

$\displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \epsilon_{\eta} }{ \tau } + \displaystyle\frac{ \epsilon_{ \rho } }{ \tau }$

Conditions

Variables

$\epsilon_{\rho}$

Energy dissipated by flotation

$J$

9487

$\epsilon_{\eta}$

Energy dissipated by viscosity

$J$

9486

$\epsilon_v$

Kinetic energy

$J$

9492

Relation

ID:(12205, 0)

Equation

>Top, >Model

With the vortex speed ($v_l$) and the mixing length ($l$), one can define a characteristic time ($\tau$), which allows estimating the energy loss both due to viscosity and flotation.

Therefore, it follows that

$\tau = \displaystyle\frac{ l }{ v_l }$

Conditions

Variables

$\tau$

Characteristic time

$s$

9491

$l$

Mixing length

$m$

9489

$v_l$

Vortex speed

$m/s$

9490

Relation

ID:(12206, 0)

Equation

>Top, >Model

The variation of the kinetic energy ($\epsilon_v$) in the characteristic time ($\tau$) is proportional to the kinetic energy, which depends on the medium density ($\rho$) and the vortex speed ($v_l$), divided by the characteristic time ($\tau$). Since this is a function of the mixing length ($l$), it follows that:

$\displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$

Conditions

Variables

$\tau$

Characteristic time

$s$

9491

$\epsilon_v$

Kinetic energy

$J$

9492

$\rho$

Medium density

$kg/m^3$

9096

$l$

Mixing length

$m$

9489

$v_l$

Vortex speed

$m/s$

9490

Relation

Development

Como the kinetic energy ($\epsilon_v$) of the vortices depends on the medium density ($\rho$) and the vortex speed ($v_l$) according to

$\epsilon_v =\displaystyle\frac{1}{2}\rho v_l^2\sim \rho v_l^2$

Como the characteristic time ($\tau$) with the mixing length ($l$) is

$\tau = \displaystyle\frac{ l }{ v_l }$

we have that

$\displaystyle\frac{\epsilon_v}{\tau} =\rho \displaystyle\frac{v_l^3}{l}$

which means

$\displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$

ID:(12212, 0)

Equation

>Top, >Model

The loss due to water viscosity can be calculated directly from the viscous force and the path traveled by the vortex.

The loss of the energy dissipated by viscosity ($\epsilon_{\eta}$) varies depending on the viscosity of ocean water ($\eta$), the vortex speed ($v_l$), and the mixing length ($l$). In the characteristic time ($\tau$), it is expressed as

$\displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$

Conditions

Variables

$\tau$

Characteristic time

$s$

9491

$\epsilon_{\eta}$

Energy dissipated by viscosity

$J$

9486

$l$

Mixing length

$m$

9489

$\eta$

Viscosity of ocean water

$Pa s$

8612

$v_l$

Vortex speed

$m/s$

9490

Relation

Development

The loss from the vortices involves the energy dissipated by viscosity ($\epsilon_{\eta}$) with the viscosity of ocean water ($\eta$), the vortex speed ($v_l$), and the mixing length ($l$).

$\epsilon_{\eta} =\eta\displaystyle\frac{v_l}{l}$

The energy loss due to the characteristic time ($\tau$), which is

$\tau = \displaystyle\frac{ l }{ v_l }$

is described by

$\displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$

ID:(12207, 0)

Equation

>Top, >Model

The loss due to buoyancy can be calculated directly from the lift force and the distance traveled by the vortex.

The loss of the energy dissipated by flotation ($\epsilon_{\rho}$) varies depending on the variación de la densidad ($\Delta\rho$), the gravitational Acceleration ($g$), and the vortex speed ($v_l$). In the characteristic time ($\tau$), it is expressed as

$\displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l$

Conditions

Variables

$\tau$

Characteristic time

$s$

9491

$\epsilon_{\rho}$

Energy dissipated by flotation

$J$

9487

$g$

Gravitational Acceleration

9.8

$m/s^2$

5310

$\Delta\rho$

Variación de la densidad

$kg/m^3$

9484

$v_l$

Vortex speed

$m/s$

9490

Relation

Development

Since the energy dissipated by flotation ($\epsilon_{\rho}$) equals the variación de la densidad ($\Delta\rho$), the gravitational Acceleration ($g$), and the distance traveled ($\Delta z$),

$\epsilon_{\rho} =\Delta\rho g \Delta z$

the energy loss will be this energy per the characteristic time ($\tau$), which, with the mixing length ($l$), is

$\tau = \displaystyle\frac{ l }{ v_l }$

so with the vortex speed ($v_l$), it is

$\displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l$

ID:(12208, 0)

Equation

>Top, >Model

In the event that with the kinetic energy ($\epsilon_v$), the energy dissipated by viscosity ($\epsilon_{\eta}$), and the energy dissipated by flotation ($\epsilon_{\rho}$) are such that

$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$

the damping is primarily due to viscosity.

In that case, a condition is obtained for the reynolds number ($Re$), which is a function of the medium density ($\rho$), the vortex speed ($v_l$), the tamaño característico ($l$), and the viscosity of ocean water ($\eta$), which must satisfy

$Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$

Conditions

Variables

$\rho$

Medium density

$kg/m^3$

9096

$Re$

Reynolds number

$-$

9107

$l$

Tamaño característico

$m$

9112

$\eta$

Viscosity of ocean water

$Pa s$

8612

$v_l$

Vortex speed

$m/s$

9490

Relation

Development

In the case where diffusive processes are more relevant than buoyancy, we have that with the kinetic energy ($\epsilon_v$), the energy dissipated by flotation ($\epsilon_{\rho}$) and the energy dissipated by viscosity ($\epsilon_{\eta}$),

$\epsilon_v > \epsilon_{\eta} \gg \epsilon_{\rho}$

Given that with the characteristic time ($\tau$), the kinetic energy ($\epsilon_v$) and the medium density ($\rho$) is

$\displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$

and the energy dissipated by viscosity ($\epsilon_{\eta}$) is

$\displaystyle\frac{ \epsilon_{\eta} }{ \tau } = \eta \displaystyle\frac{ v_l ^2 }{ l ^2 }$

the existence of the vortex implies that its kinetic energy is greater than the loss, so with

$\rho\displaystyle\frac{v_l^3}{l}>\eta\displaystyle\frac{v_l^2}{l^2}$

the requirement that the reynolds number ($Re$) must be

$Re = \displaystyle\frac{ \rho l v_l }{ \eta } > 1$

ID:(12209, 0)

Equation

>Top, >Model

In the event that with the kinetic energy ($\epsilon_v$), the energy dissipated by viscosity ($\epsilon_{\eta}$), and the energy dissipated by flotation ($\epsilon_{\rho}$) are such that

$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$

the damping is primarily due to buoyancy.

In that case, a condition is obtained for the richardson number ($R_i$), which is a function of the variación de la densidad ($\Delta\rho$), the medium density ($\rho$), the vortex speed ($v_l$), the gravitational Acceleration ($g$), and the mixing length ($l$), which must satisfy

$R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$

Conditions

Variables

$g$

Gravitational Acceleration

9.8

$m/s^2$

5310

$\rho$

Medium density

$kg/m^3$

9096

$l$

Mixing length

$m$

9489

$R_i$

Richardson number

$-$

9494

$\Delta\rho$

Variación de la densidad

$kg/m^3$

9484

$v_l$

Vortex speed

$m/s$

9490

Relation

Development

In the event that with the kinetic energy ($\epsilon_v$), the energy dissipated by viscosity ($\epsilon_{\eta}$), and the energy dissipated by flotation ($\epsilon_{\rho}$) are such that

$\epsilon_v > \epsilon_{\rho} \gg \epsilon_{\eta}$

Given that the kinetic energy ($\epsilon_v$) is with the medium density ($\rho$), the mixing length ($l$), and the vortex speed ($v_l$) in the characteristic time ($\tau$),

$\displaystyle\frac{ \epsilon_v }{ \tau } = \displaystyle\frac{ \rho v_l ^3 }{ l }$

and the energy dissipated by flotation ($\epsilon_{\rho}$) is with the variación de la densidad ($\Delta\rho$), the gravitational Acceleration ($g$), and the vortex speed ($v_l$) in the characteristic time ($\tau$),

$\displaystyle\frac{ \epsilon_{\rho} }{ \tau } = \Delta\rho g v_l$

the existence of the vortex implies that its kinetic energy is greater than the loss, so with

$\rho\displaystyle\frac{v_l^3}{l}>\Delta\rho g v_l$

the requirement arises that with, the richardson number ($R_i$) must satisfy

$R_i = \displaystyle\frac{\Delta \rho}{\rho}\displaystyle\frac{ g l }{ v_l^2}<1$

ID:(12210, 0)