Benützer: 
Molekularer Transport von Momentum
Storyboard 
Angesichts eines Impulsunterschieds werden Prozesse des Molekülaustauschs erzeugt, die dazu führen, dass Moleküle von Bereichen mit größerem zu Bereichen mit geringerem Moment gelangen, was letztendlich zu einem homogenen Moment führt.
ID:(1606, 0)
Difusión de momento
Bild
Uno de los procesos de difusión que ocurren en el océano es el del momento que se expresa como velocidad del agua. Físicamente corresponde a la difusión de partículas que tienen diferencia momento/velocidad.
ID:(12151, 0)
Diffusionskonstante des Momentums
Gleichung
Die Bewegung eines Systems wie Wasser neigt dazu, sich zu verbreiten, bis das System in Bezug auf seine Umgebung zur Ruhe kommt. Dieses Phänomen wird als Viskosität bezeichnet und konkurriert mit der Trägheit von Körpern, um die Bewegung aufrechtzuerhalten.
Der erste Begriff ist mit die Viskosität von Meerwasser (\eta) verbunden, während der zweite mit der Masse oder im Fall einer Flüssigkeit mit die Dichte des Meerwassers (\rho) zusammenhängt.
Daher führen wir die Diffusionskonstante des Moments (D_p) ein mit:
 D_p \equiv \displaystyle\frac{ \eta }{ \rho } |
Die Einheiten sind:
\displaystyle\frac{\eta}{\rho} \rightarrow \displaystyle\frac{Pa,s}{kg/m^3} = \displaystyle\frac{m^3 kg,m,s}{s^2m^2kg} = \displaystyle\frac{m^2}{s}
was einer Diffusionskonstante entspricht. Der Wert für Wasser liegt in der Größenordnung von 10^{-6} , m^2/s.
ID:(12049, 0)
Flujo de componente de momento
Gleichung
Si existe en un punto
\Delta u_i = u_i(x_i+\Delta x_i)-u_i(x_i)
\\n\\nun gradiente\\n\\n
\displaystyle\frac{u_i(x_i+\Delta x_i)-u_i(x_i)}{\Delta x_i}=\displaystyle\frac{\Delta u_i}{\Delta z}\sim\displaystyle\frac{\partial u_i}{\partial x_i}
que llevara a que se genere un flujo de la zona de mayor a menor velocidad. Esto simplemente porque existen mas moléculas en la zona de mayor velocidad que en la con menor. El flujo que se genera es proporcional a dicho gradiente que depende de la movilidad que tengan los iones. Por ello se puede establecer con que
| q_{u,i} = \eta \displaystyle\frac{\partial u_i }{\partial x_i } |
ID:(12137, 0)
Flujo medio del momento
Gleichung
Si el flujo de momento es coordenada i de la densidad de flujo de momento Pa, coordenada i de la posición m, coordenada i de la velocidad m/s und viskosität von Meerwasser Pa s que
| q_{u,i} = \eta \displaystyle\frac{\partial u_i }{\partial x_i } |
en el caso medio se puede expresar con variaciones finitas de modo de que con coordenada i de la densidad de flujo de momento Pa, coordenada i de la posición m, coordenada i de la velocidad m/s und viskosität von Meerwasser Pa s es
| q_{ui} = \eta \displaystyle\frac{ \Delta u_i }{ \Delta x_i } |
ID:(12163, 0)
Valores de la viscosidad dinámica del agua marina
Bild
La viscosidad dinámica es una función de la temperatura del agua marina. Esta disminuye en forma importante con el aumento de la temperatura.
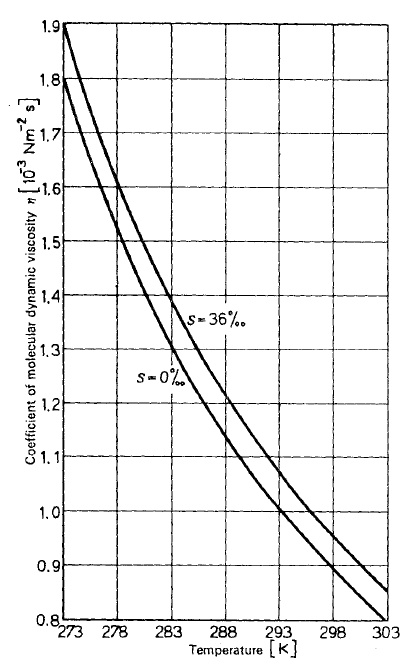
ID:(12161, 0)
Variación temporal de la velocidad
Gleichung
Lo que corresponde a la variación de la concentración que
| \displaystyle\frac{\partial c }{\partial t } = -\displaystyle\frac{\partial j }{\partial z } |
\\n\\ncorresponde ahora a la variación de la densidad de momento que es la densidad multiplicado por la densidad y la variación de la velocidad\\n\\n
du_i = \rho du_i
por lo que se puede describir la dinámica con mediante
| \rho \displaystyle\frac{\partial u_i }{\partial t } = \displaystyle\frac{\partial q_{u,i} }{\partial x_i } |
ID:(12156, 0)
Variación temporal media de la velocidad
Gleichung
Si la variación temporal de la temperatura instantánea es coordenada i de la densidad de flujo de momento Pa, coordenada i de la posición m, coordenada i de la velocidad m/s, dichte kg/m^3 und tiempo s que
| \rho \displaystyle\frac{\partial u_i }{\partial t } = \displaystyle\frac{\partial q_{u,i} }{\partial x_i } |
en el caso medio se puede expresar con variaciones finitas de modo de que con coordenada i de la densidad de flujo de momento Pa, coordenada i de la posición m, coordenada i de la velocidad m/s, dichte kg/m^3 und tiempo s es
| \rho \displaystyle\frac{\Delta u_i }{\Delta t } = \displaystyle\frac{\Delta q_{u,i} }{\Delta x_i } |
ID:(12165, 0)
Ley de Fick para viscosidad dinámica constante
Gleichung
Como la primera ley de Fick en este caso es con coordenada i de la densidad de flujo de momento Pa, coordenada i de la posición m, coordenada i de la velocidad m/s und viskosität von Meerwasser Pa s
| q_{u,i} = \eta \displaystyle\frac{\partial u_i }{\partial x_i } |
y la segunda ley de Fick en este caso es con coordenada i de la densidad de flujo de momento Pa, coordenada i de la posición m, coordenada i de la velocidad m/s, dichte kg/m^3 und tiempo s igual a
| \rho \displaystyle\frac{\partial u_i }{\partial t } = \displaystyle\frac{\partial q_{u,i} }{\partial x_i } |
se tiene la ley general de Fick para el caso de que la viscosidad dinámica no varíe con la posición que con coordenada i de la densidad de flujo de momento Pa, coordenada i de la posición m, coordenada i de la velocidad m/s, dichte kg/m^3 und tiempo s es igual a
| \displaystyle\frac{\partial u_i }{\partial t } = \displaystyle\frac{ \eta }{ \rho } \displaystyle\frac{\partial^2 u_i }{\partial x_i ^2 } |
ID:(12164, 0)
Distribución de momento en el tiempo
Gleichung
Para el caso del momento constante la ley general de Fick con coordenada i de la posición m, coordenada i de la velocidad m/s, dichte kg/m^3, tiempo s und viskosität von Meerwasser Pa s
| \displaystyle\frac{\partial u_i }{\partial t } = \displaystyle\frac{ \eta }{ \rho } \displaystyle\frac{\partial^2 u_i }{\partial x_i ^2 } |
se logra resolver esta ecuación obtenerse con coordenada i de la posición m, coordenada i de la velocidad m/s, dichte kg/m^3, tiempo s und viskosität von Meerwasser Pa s la expresión
| u_i =\displaystyle\frac{1}{\sqrt{4 \pi \eta t / \rho }} e^{- \rho x_i ^2 /4 \eta t } |
ID:(12162, 0)
0
Video
Video: Transporte Molecular de Momento