Utilizador:
Mecanismos
Iframe 
Mecanismos
ID:(15457, 0)
Geração de som
Descrição
O som é produzido quando uma superfície se move, aumentando ou diminuindo o volume de gás.
No primeiro caso, as moléculas ao redor ocupam o novo espaço, criando uma zona de menor densidade do ar que será preenchida por outras moléculas vizinhas.
No segundo caso, as moléculas ao redor são comprimidas, resultando em um deslocamento para regiões de menor densidade.
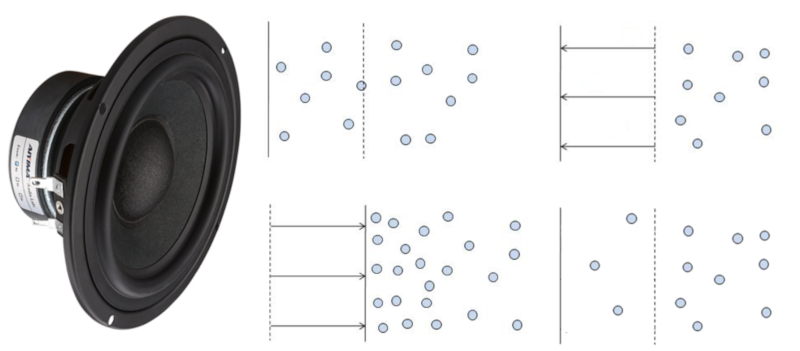
Ambas as mudanças levam à propagação de reduções ou aumentos na densidade, o que corresponde a uma onda sonora.
ID:(1670, 0)
Movimento de moléculas
Descrição
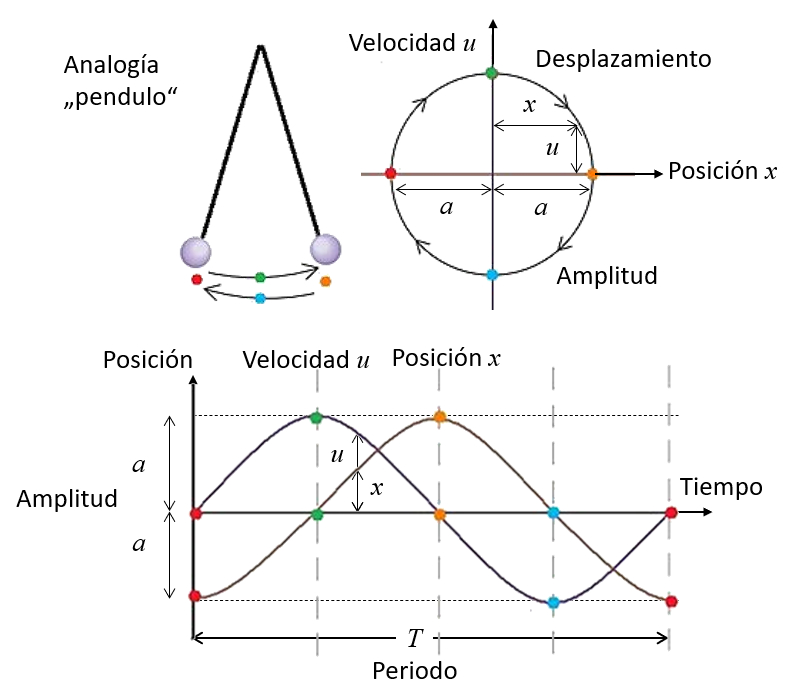
A oscilação de uma molécula devido a uma onda sonora pode ser descrita em termos de sua posição e velocidade.
Se ambas forem representadas como arestas em um gráfico, pode-se observar uma trajetória elíptica. Nos pontos extremos verticais, a partícula atinge velocidade máxima, sendo positiva em uma extremidade (movendo-se da esquerda para a direita) e negativa na outra extremidade (movendo-se da direita para a esquerda). Nos pontos extremos horizontais, encontra-se a amplitude, sendo que o ponto da esquerda indica um valor mínimo e o ponto da direita indica um valor positivo.
Da mesma forma, essas oscilações podem ser representadas como uma função de tempo ($t$)5264,0. Se partirmos de um ponto onde ($$)5075 é inicialmente negativo e máximo, a velocidade é descrita por uma função seno, enquanto la tempo ($x$)5074 é descrita por uma função cosseno que inicialmente tem uma amplitude negativo. Porém, esta escolha é arbitrária, pois o ciclo pode começar a partir de qualquer outro ponto, por exemplo, quando a amplitude é inicialmente zero, como é o caso quando a onda sonora chega. Neste último caso, a posição é modelada com uma função senoidal.
ID:(3187, 0)
Propagação do som
Descrição
O som é gerado quando uma superfície se move, aumentando ou diminuindo o volume de um gás circundante.
Uma vez que ocorre uma variação de densidade/pressão, ela se propaga com a velocidade da onda ($c$)9752,0:
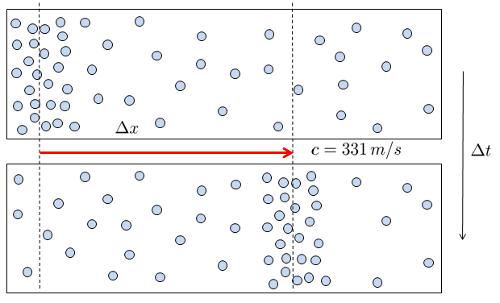
Por essa razão, somos capazes de ouvir o som produzido por um alto-falante.
É importante reconhecer:
O som requer um meio no qual ocorra variação de densidade/pressão, seja ele gás, líquido ou sólido. Portanto, o som não pode se propagar no vácuo.
ID:(11795, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ c = \lambda \nu $
c = lambda * nu
$ c = \displaystyle\frac{ \lambda }{ T }$
c = lambda / T
$ \nu =\displaystyle\frac{1}{ T }$
nu =1/ T
$\omega=2\pi\nu$
omega =2* pi * nu
$ u = a \omega $
u = a * omega
$ x = a \cos( \omega t )$
x = a * cos( omega * t )
ID:(15452, 0)
Oscilação de moléculas
Equação
O movimento médio gerado pela onda sonora corresponde a uma oscilação em torno da posição original da molécula.
Essa oscilação pode ser descrita usando uma função trigonométrica que envolve uma amplitude $a$, uma frequência angular $\omega$ e o tempo $t$.
A oscilação é descrita da seguinte maneira:
| $ x = a \cos( \omega t )$ |
ID:(3392, 0)
Frequência
Equação
La frequência ($\nu$)5077 corresponde ao número de vezes que ocorre uma oscilação em um segundo. Já La período ($T$)5078 é o tempo que uma única oscilação leva. Portanto, o número de oscilações por segundo é:
| $ \nu =\displaystyle\frac{1}{ T }$ |
A frequência é indicada em Hertz (Hz).
ID:(4427, 0)
Velocidade das moléculas
Equação
Se observarmos o diagrama de velocidade versus posição, podemos interpretar a oscilação como um movimento circular nesse diagrama. Nesse caso, podemos estimar ($$)5715 como o perímetro, que é a distância percorrida dividida pelo tempo decorrido, que é La período ($T$)5078. Se ($$)5075 for o raio, então com la frequência angular ($\omega$)9010:
$u=\displaystyle\frac{2\pi a}{T}=a\omega$
Isso significa que ($$)5715 é:
| $ u = a \omega $ |
ID:(3395, 0)
Comprimento da onda e velocidade da onda
Equação
La velocidade da onda ($c$)9752 é uma velocidade, o que significa que é igual a uma extensão, como la comprimento de onda ($\lambda$)9772, dividida pelo tempo que uma oscilação leva para avançar, ou seja, ($$)9741. Portanto, temos:
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
ID:(12378, 0)
Velocidade, comprimento e frequência da onda
Equação
La concentração molar ($c$)5073 é uma velocidade, o que significa que é igual a uma extensão, como o comprimento da onda sonora ($\lambda$)5079, dividida pelo tempo que uma oscilação leva para avançar. Como o inverso do tempo é La frequência ($\nu$)5077, temos:
| $ c = \lambda \nu $ |
La concentração molar ($c$)5073 com o comprimento da onda sonora ($\lambda$)5079 e la período ($T$)5078 é expresso como
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
e pode ser reescrito com la frequência ($\nu$)5077 como
| $ \nu =\displaystyle\frac{1}{ T }$ |
assim, obtendo a relação
| $ c = \lambda \nu $ |
ID:(12384, 0)