Usuario:
Mecanismos
Iframe 
Mecanismos
ID:(15457, 0)
Generación de sonido
Descripción
El sonido se produce cuando una superficie se mueve, ya sea aumentando o disminuyendo el volumen de gas.
En el primer caso, las moléculas circundantes ocuparán el nuevo espacio, creando una zona de menor densidad de aire que será llenada por otras moléculas vecinas.
En el segundo caso, las moléculas circundantes se comprimen, lo que resulta en un desplazamiento hacia regiones de menor densidad.
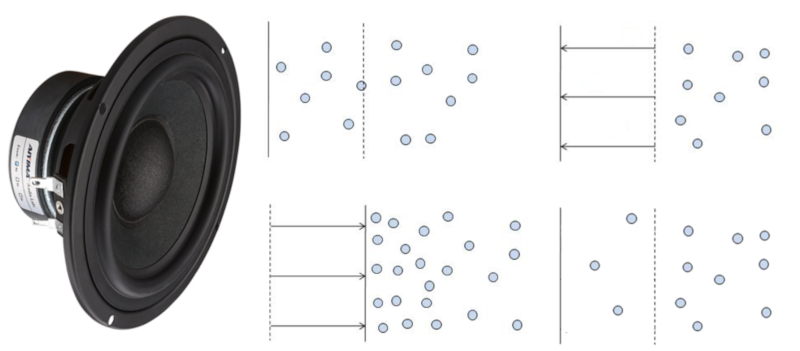
Ambos cambios llevan a la propagación de reducciones o aumentos en la densidad, lo cual corresponde a una onda de sonido.
ID:(1670, 0)
Movimiento de las moléculas
Descripción
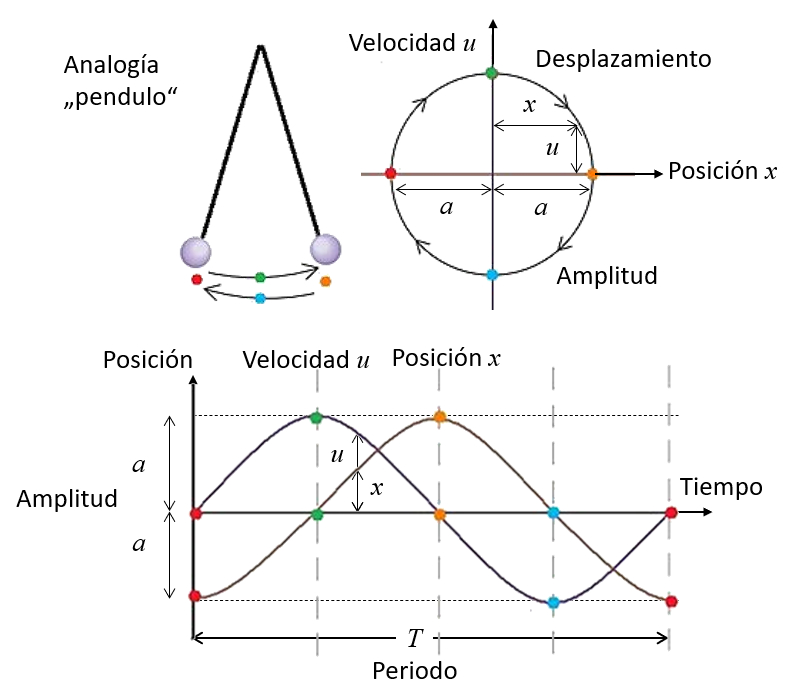
La oscilación de una molécula debido a una onda sonora puede describirse en términos de su posición y velocidad.
Si representamos ambas en un gráfico, se observa una trayectoria elipsoidal. En los puntos verticales extremos, la partícula alcanza una velocidad máxima, siendo positiva en un extremo (viajando de izquierda a derecha) y negativa en el otro extremo (viajando de derecha a izquierda). En los puntos horizontales extremos se encuentra la amplitud, donde el punto izquierdo representa el mínimo y el punto derecho, el máximo.
Del mismo modo, estas oscilaciones pueden representarse en función del tiempo ($t$)5264,0. Si comenzamos desde un punto donde la amplitud de la Oscilación de la Molécula ($a$)5075 es inicialmente negativa y máxima, la velocidad se describe mediante una función seno, mientras que la posición media de la Molécula ($x$)5074 se describe con una función coseno que inicialmente tiene una amplitud negativa. Sin embargo, esta elección es arbitraria, ya que el ciclo puede comenzar desde cualquier otro punto, por ejemplo, cuando la amplitud es inicialmente cero, como ocurre cuando llega la onda sonora. En este último caso, la posición se modela con una función seno.
ID:(3187, 0)
Propagación de sonido
Descripción
El sonido se produce cuando una superficie se desplaza, ya sea aumentando o disminuyendo el volumen de un gas circundante.
Una vez que se ha generado una variación en la densidad o presión, esta se propaga a través del medio a la velocidad de la onda ($c$)9752:
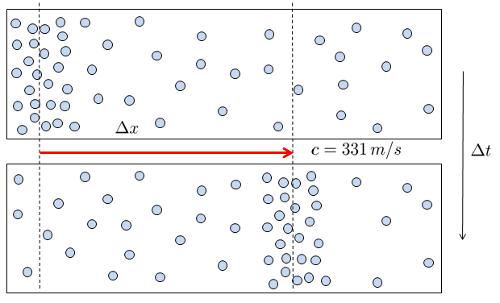
Altoparlante
Es por esta razón que somos capaces de escuchar el sonido emitido por un altavoz.
Es importante tener en cuenta lo siguiente:
El sonido requiere de un medio en el cual varíe la densidad o presión, ya sea gas, líquido o sólido. Por lo tanto, el sonido no puede propagarse en el vacío.
ID:(11795, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ c = \lambda \nu $
c = lambda * nu
$ c = \displaystyle\frac{ \lambda }{ T }$
c = lambda / T
$ \nu =\displaystyle\frac{1}{ T }$
nu =1/ T
$\omega=2\pi\nu$
omega =2* pi * nu
$ u = a \omega $
u = a * omega
$ x = a \cos( \omega t )$
x = a * cos( omega * t )
ID:(15452, 0)
Oscilación de las moléculas
Ecuación
El movimiento promedio generado por la onda sonora corresponde a una oscilación alrededor de la posición original de la molécula.
la posición media de la Molécula ($x$)5074 puede ser descrita mediante una función trigonométrica que involucra una amplitud de la Oscilación de la Molécula ($a$)5075,1, una frecuencia angular ($\omega$)9743,1 y el tiempo ($t$)5264.
La oscilación se describe de la siguiente manera:
| $ x = a \cos( \omega t )$ |
ID:(3392, 0)
Frecuencia
Ecuación
La frecuencia ($\nu$)5077 representa la cantidad de oscilaciones que ocurren en un segundo. Mientras tanto, la período ($T$)5078 es el tiempo que tarda una sola oscilación. Por lo tanto, el número de oscilaciones por segundo es:
| $ \nu =\displaystyle\frac{1}{ T }$ |
La frecuencia se expresa en Hertz (Hz).
ID:(4427, 0)
Velocidad de las moléculas
Ecuación
Si se observa el diagrama de velocidad versus posición se puede entender la oscilación como un movimiento circular en dicho diagrama. En ese caso se puede estimar la velocidad media de las moleculas ($u$)5715 como el perímetro como camino recorrido dividido por el tiempo transcurrido que es la período ($T$)5078. Si la amplitud de la Oscilación de la Molécula ($a$)5075 es el radio se tiene que con la frecuencia angular ($\omega$)9010:
$u=\displaystyle\frac{2\pi a}{T}=a\omega$
O sea que la velocidad media de las moleculas ($u$)5715 es
| $ u = a \omega $ |
ID:(3395, 0)
Largo de onda y velocidad de la onda
Ecuación
La velocidad de la onda ($c$)9752 es una velocidad, lo que significa que es igual a una longitud, como la largo de onda ($\lambda$)9772, dividida por el tiempo que tarda una oscilación en avanzar, es decir, la periodo del resorte ($T$)9741. Por lo tanto, obtenemos:
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
ID:(12378, 0)
Velocidad, largo y frecuencia de la onda
Ecuación
La velocidad del sonido ($c$)5073 es una velocidad, lo que significa que es igual a una longitud, como el largo de Onda de Sonido ($\lambda$)5079, dividida por el tiempo que tarda una oscilación en avanzar. Dado que el inverso del tiempo es la frecuencia ($\nu$)5077, podemos expresarlo como:
| $ c = \lambda \nu $ |
La velocidad del sonido ($c$)5073 con el largo de Onda de Sonido ($\lambda$)5079 y la período ($T$)5078 se expresa como
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
y puede ser reescrita con la frecuencia ($\nu$)5077 como
| $ \nu =\displaystyle\frac{1}{ T }$ |
lo que nos da la relación
| $ c = \lambda \nu $ |
ID:(12384, 0)
Velocidad angular y frecuencia
Ecuación
La frecuencia angular ($\omega$)9010 se puede calcular de la frecuencia ($\nu$)5077 y el pi ($\pi$)5057 con
| $\omega=2\pi\nu$ |
Con la frecuencia angular ($\omega$)9010 que se calcula con el pi ($\pi$)5057 y la período ($T$)5078 mediante
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
y con la frecuencia ($\nu$)5077 y la período ($T$)5078
| $ \nu =\displaystyle\frac{1}{ T }$ |
se puede reescribir como
| $\omega=2\pi\nu$ |
ID:(3589, 0)