Utilizador:
Pressão sonora
Descrição 
À medida que o som se propaga, ele provoca o deslocamento das moléculas na borda do sistema, levando a impactos contra a parede. Esses impactos transferem momento para a parede, resultando em uma força. Como a força é gerada por um grande número de partículas, seu efeito depende da área de superfície do sistema, o que gera uma pressão.
É importante entender que a pressão sonora não é igual à pressão ambiente. No ar, esta última está na ordem de $10^5,Pa$, enquanto a pressão sonora geralmente é muito menor que $1,Pa$.
ID:(134, 0)
Formação de pressão
Conceito
Se deslocarmos a face de um cubo, geramos um aumento ou diminuição da concentração, o que leva a uma diminuição ou aumento das colisões das moléculas com a face do volume:
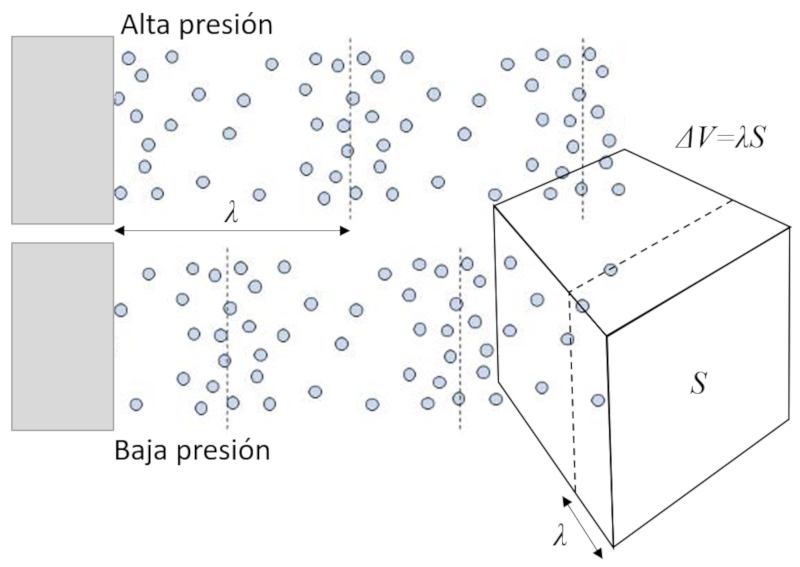
Como a pressão é a transferência de momento devido às colisões das moléculas com a parede, a variação do volume leva a um aumento ou diminuição da pressão.
ID:(1865, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ \Delta V = S \lambda $
DV = S * lambda
$ F =\displaystyle\frac{ d p }{ d t }$
F = dp / dt
$ L = 20 \log_{10}\left(\displaystyle\frac{ p }{ p_{ref} }\right)$
L = 20* log10( p / p_ref )
$ p \equiv\displaystyle\frac{ F }{ S }$
p = F / S
$ p = \rho c u $
p = rho * c * u
$ Z =\displaystyle\frac{ p }{ u }$
Z = p / u
$ Z = \rho c $
Z = rho * c
ID:(15453, 0)
Definição de pressão
Equação
La pressão da coluna de água ($p$)10114 é calculado a partir de la força da coluna ($F$)10113 e la altura da coluna líquida ($S$)6002 da seguinte forma:
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
ID:(4342, 0)
Força exercida pelas moléculas
Equação
Segundo Newton, a força pode ser expressa como a variação de ($$)9047,0. Esse momento é gerado pelo rebote das partículas, que transferem momento para a parede. Dado que o momento é conservado e o momento da partícula ao quicar muda de $p_{partícula}$ para $-p_{partícula}$, pela conservação do momento temos então:
$p_{\text{partícula}} = p_{\text{parede}} - p_{\text{partícula}}$
o que implica em
$p_{\text{parede}} = 2p_{\text{partícula}}$
Dessa forma, a variação de ($$)9047 na parede é de o tempo ($t$)5264 e gera ($$)5085,1, que é
| $ F =\displaystyle\frac{ d p }{ d t }$ |
ID:(3390, 0)
Volume com moléculas
Equação
Quando uma onda sonora atravessa um volume com moléculas ($\Delta V$)5080,1, ela se expande e contrai ao longo de uma distância da ordem de um comprimento da onda sonora ($\lambda$)5079,1, resultando em uma variação de volume que depende de la seção ou superfície ($S$)5405 perpendicular à direção de propagação.
Portanto, a variação de volume é igual a:
| $ \Delta V = S \lambda $ |
ID:(3398, 0)
Variação do momento por moléculas
Equação
La pressão sonora ($p$)5084 pode ser entendido como a densidade de momento calculada a partir de la densidade média ($\rho$)5088 e la velocidade da molécula ($u$)5072, que é então multiplicada por la concentração molar ($c$)5073 através de
| $ p = \rho c u $ |
A variação do momento $dp$ está associada à massa das moléculas $m$ e à velocidade do som $u$ das moléculas através de:
$dp = 2mu \approx mu$
Assim, em um intervalo de tempo igual ao período $dt \approx T$, temos:
$F=\displaystyle\frac{dp}{dt}=\displaystyle\frac{mu}{T}$
Portanto, la pressão sonora ($p$)5084 pode ser calculado usando a pressão
la concentração molar ($c$)5073 é
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
e o volume com moléculas ($\Delta V$)5080 que varia
| $ \Delta V = S \lambda $ |
da seguinte forma:
$p=\displaystyle\frac{1}{S} \displaystyle\frac{dp}{dt}=\displaystyle\frac{1}{S}\displaystyle\frac{mu}{T}=\displaystyle\frac{muc}{ScT}=\displaystyle\frac{muc}{S\lambda}=\displaystyle\frac{muc}{\Delta V}=\rho u c$
No último termo, tanto o numerador quanto o denominador são multiplicados por $c$. A expressão no denominador representa o volume do gás deslocado pelo som em $T$, então podemos substituir a massa dividida por este volume pela densidade, resultando em:
| $ p = \rho c u $ |
ID:(3391, 0)
Nível de ruído em função da pressão sonora, ar
Equação
La pressão de referência, água ($L$)5119 abrange uma ampla gama de la pressão sonora ($p$)5084, tornando útil definir uma escala que mitigue essa dificuldade. Para isso, podemos trabalhar com o logaritmo da pressão normalizado por um valor que corresponda a zero nesta escala. Se tomarmos a pressão mínima que uma pessoa pode detectar, definida como la pressão de referência ($p_{ref}$)5121, podemos definir uma escala usando:
| $ L = 20 \log_{10}\left(\displaystyle\frac{ p }{ p_{ref} }\right)$ |
que começa em 0 para o intervalo audível. No caso do ar, la pressão de referência ($p_{ref}$)5121 é de $20 \mu Pa$.
ID:(3407, 0)
Impedância acústica
Equação
O conceito de ($$)5104,0 fornece uma medida da resistência do sistema para transmitir a onda sonora. Ele considera uma pressão atuante e estabelece uma medida na qual o meio exposto é deslocado. Dessa forma, la pressão sonora ($p$)5084 é comparado com la velocidade da molécula ($u$)5072.
Portanto, ($$)5104 é definido como:
| $ Z =\displaystyle\frac{ p }{ u }$ |
ID:(3414, 0)
Impedância em ondas
Equação
Para calcular ($$)5104 a partir de la densidade média ($\rho$)5088 e la concentração molar ($c$)5073, utiliza-se a fórmula:
| $ Z = \rho c $ |
Como ($$)5104 é calculado a partir de la pressão sonora ($p$)5084 e la velocidade da molécula ($u$)5072 usando
| $ Z =\displaystyle\frac{ p }{ u }$ |
junto com a expressão para la pressão sonora ($p$)5084 em termos de la densidade média ($\rho$)5088 e la concentração molar ($c$)5073,
| $ p = \rho c u $ |
nós obtemos
| $ Z = \rho c $ |
ID:(12413, 0)