Benützer:
Mechanismen
Iframe 
Mechanismen
ID:(15457, 0)
Klangerzeugung
Beschreibung
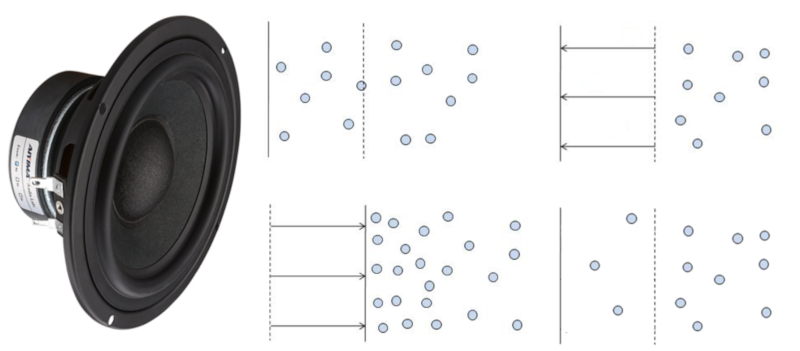
Der Klang entsteht, wenn eine Oberfläche sich bewegt und dadurch das Volumen von Gas entweder erhöht oder verringert.
Im ersten Fall besetzen die umgebenden Moleküle den neuen Raum und erzeugen eine Zone mit geringerer Luftdichte, die von anderen benachbarten Molekülen aufgefüllt wird.
Im zweiten Fall werden die umgebenden Moleküle komprimiert, was zu einer Verschiebung in Bereiche mit geringerer Dichte führt.
Altoparlante
Beide Veränderungen führen zur Ausbreitung von Dichteverringerungen oder -erhöhungen, was einer Schallwelle entspricht.
ID:(1670, 0)
Bewegung der Moleküle
Beschreibung
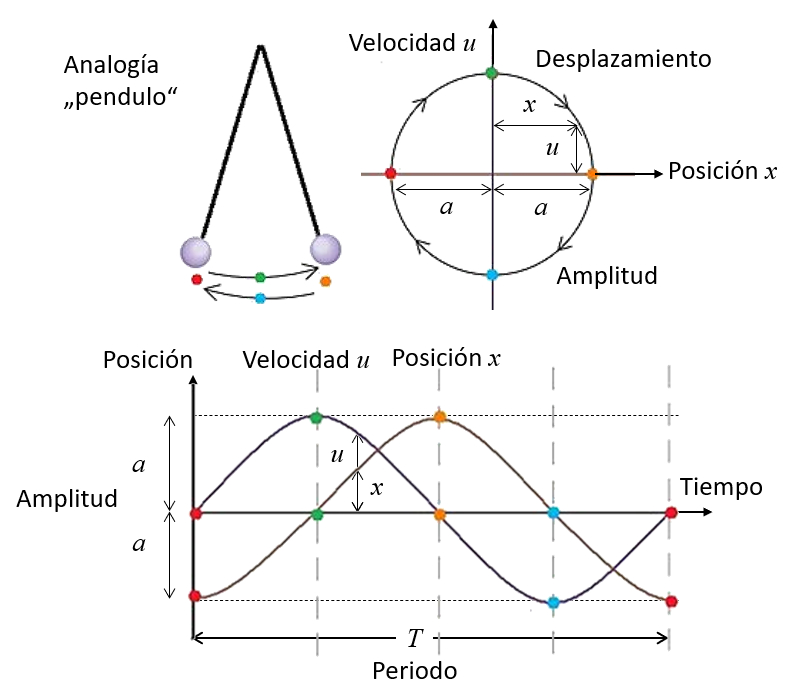
Die Schwingung eines Moleküls aufgrund einer Schallwelle kann in Bezug auf seine Position und Geschwindigkeit beschrieben werden.
Wenn beide als Kanten auf einem Diagramm dargestellt werden, ist eine elliptische Bahn zu beobachten. An den vertikalen Extrempunkten erreicht das Teilchen maximale Geschwindigkeit, wobei das eine Ende positiv ist (bewegt sich von links nach rechts) und das andere Ende negativ ist (bewegt sich von rechts nach links). Die horizontalen Extrempunkte repräsentieren die Amplitude, wobei der linke Punkt einen minimalen Wert und der rechte Punkt einen positiven Wert angibt.
Ebenso können diese Schwingungen als Funktion von der Zeit ($t$)5264.0 dargestellt werden. Wenn wir von einem Punkt ausgehen, an dem die Amplitude Oscillation Molecule ($a$)5075 anfänglich negativ und maximal ist, wird die Geschwindigkeit durch eine Sinusfunktion beschrieben, während die Durchschnittliche Position des Moleküls ($x$)5074 durch eine Kosinusfunktion beschrieben wird, die anfänglich eine Amplitude hat Negativ. Diese Wahl ist jedoch willkürlich, da der Zyklus an jedem anderen Punkt beginnen kann, beispielsweise wenn die Amplitude zunächst Null ist, wie es beim Eintreffen der Schallwelle der Fall ist. Im letzteren Fall wird die Position mit einer Sinusfunktion modelliert.
ID:(3187, 0)
Schallausbreitung
Beschreibung
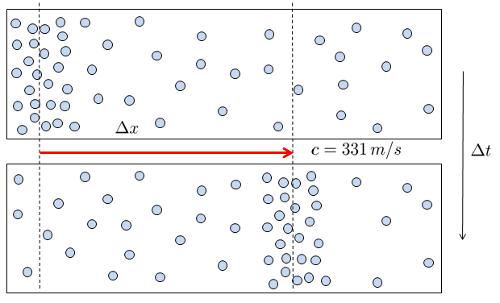
Der Klang entsteht, wenn sich eine Oberfläche bewegt und dabei das Volumen eines umgebenden Gases entweder erhöht oder verringert.
Sobald eine Dichte-/Druckänderung entstanden ist, breitet sie sich mit Wellengeschwindigkeit ($c$)9752,0 aus:
Altoparlante
Aus diesem Grund können wir den von einem Lautsprecher erzeugten Klang hören.
Es ist wichtig zu erkennen:
Der Schall erfordert ein Medium, in dem sich die Dichte/der Druck verändert, sei es Gas, Flüssigkeit oder Feststoff. Daher kann sich der Schall nicht im Vakuum ausbreiten.
ID:(11795, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ c = \lambda \nu $
c = lambda * nu
$ c = \displaystyle\frac{ \lambda }{ T }$
c = lambda / T
$ \nu =\displaystyle\frac{1}{ T }$
nu =1/ T
$\omega=2\pi\nu$
omega =2* pi * nu
$ u = a \omega $
u = a * omega
$ x = a \cos( \omega t )$
x = a * cos( omega * t )
ID:(15452, 0)
Swingung der Moleküle
Gleichung
Die durch die Schallwelle erzeugte mittlere Bewegung entspricht einer Schwingung um die ursprüngliche Position des Moleküls.
Diese Schwingung kann mithilfe einer trigonometrischen Funktion beschrieben werden, die eine Amplitude $a$, eine Winkelgeschwindigkeit $\omega$ und die Zeit $t$ beinhaltet.
Die Schwingung wird wie folgt beschrieben:
| $ x = a \cos( \omega t )$ |
ID:(3392, 0)
Frequenz
Gleichung
Die Frequenz ($\nu$)5077 entspricht der Anzahl der Schwingungen, die innerhalb einer Sekunde auftreten. Die Zeit ($T$)5078 repräsentiert die Zeit, die für eine einzelne Schwingung benötigt wird. Daher ist die Anzahl der Schwingungen pro Sekunde:
| $ \nu =\displaystyle\frac{1}{ T }$ |
Die Frequenz wird in Hertz (Hz) angegeben.
ID:(4427, 0)
Geschwindigkeit der Moleküle
Gleichung
Wenn wir das Geschwindigkeits-gegen-Position-Diagramm betrachten, können wir die Schwingung als eine kreisförmige Bewegung in diesem Diagramm interpretieren. In diesem Fall können wir Velocidad media de las moleculas ($u$)5715 als den Umfang schätzen, der die zurückgelegte Strecke durch die vergangene Zeit, die Zeit ($T$)5078, geteilt ist. Wenn die Amplitude Oscillation Molecule ($a$)5075 der Radius ist, dann mit die Winkelfrequenz ($\omega$)9010:
$u=\displaystyle\frac{2\pi a}{T}=a\omega$
Das bedeutet, dass Velocidad media de las moleculas ($u$)5715 ist:
| $ u = a \omega $ |
ID:(3395, 0)
Wellenlänge und Wellengeschwindigkeit
Gleichung
Die Wellengeschwindigkeit ($c$)9752 ist eine Geschwindigkeit, was bedeutet, dass sie gleich einer Länge wie die Wellenlänge ($\lambda$)9772 ist, geteilt durch die Zeit, die eine Schwingung benötigt, um voranzuschreiten, also die Periodo del resorte ($T$)9741. Daher haben wir:
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
ID:(12378, 0)
Wellengeschwindigkeit, Länge und Frequenz
Gleichung
Die Speed of Sound ($c$)5073 ist eine Geschwindigkeit, was bedeutet, dass sie gleich einer Länge, wie der Wellenlänge des Schalles ($\lambda$)5079, geteilt durch die Zeit ist, die eine Schwingung benötigt, um voranzuschreiten. Da das Inverse der Zeit die Frequenz ($\nu$)5077 ist, haben wir:
| $ c = \lambda \nu $ |
Die Speed of Sound ($c$)5073 mit der Wellenlänge des Schalles ($\lambda$)5079 und die Zeit ($T$)5078 wird ausgedrückt als
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
und kann mit die Frequenz ($\nu$)5077 umgeschrieben werden als
| $ \nu =\displaystyle\frac{1}{ T }$ |
somit erhalten wir die Beziehung
| $ c = \lambda \nu $ |
ID:(12384, 0)
Winkelgeschwindigkeit und Frequenz
Gleichung
Con la frecuencia angular es
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
y con frequenz $Hz$ und zeit $s$ la frecuencia
| $ \nu =\displaystyle\frac{1}{ T }$ |
se puede reescribir con frequenz $Hz$ und zeit $s$ la frecuencia angular es
| $\omega=2\pi\nu$ |
ID:(3589, 0)