Benützer:
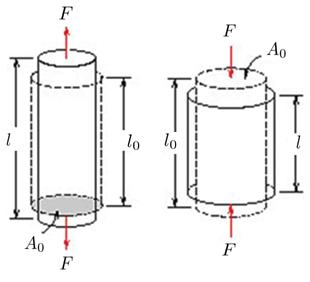
Hooke-Kraft eines Objekts
Gleichung 
Da das Hookesche Gesetz die Federkraft ($F_k$) durch die Hookes Konstante ($k$) und die Verlängerung ($u$) auf folgende Weise in Beziehung setzt:
| $ F_k = k u $ |
kann man die Hookes Konstante ($k$) durch den mikroskopischen Ausdruck ersetzen und unter Verwendung der Definition von der Elastizitätsmodul ($E$) ergibt sich mit der Körperlänge ($L$) und die Körper Sektion ($S$), dass:
 $ F_k =\displaystyle\frac{ E S }{ L } u $ |
Mit dem Hookeschen Gesetz für die Federkraft ($F_k$), die Hookes Konstante ($k$) und die Verlängerung ($u$) wie folgt:
| $ F_k = k u $ |
und dem Ausdruck für die Hookes Konstante ($k$) in Bezug auf der Körperlänge ($L$), die Körper Sektion ($S$), der Mikroskopische Länge des Frühlings ($l$), die Mikroskopische Abschnitt des Frühlings ($s$) und die Mikroskopische Hook-Konstante ($k_m$):
| $ k =\displaystyle\frac{ S }{ L }\displaystyle\frac{ l }{ s } k_m $ |
in Kombination mit dem Ausdruck für der Elastizitätsmodul ($E$):
| $ E =\displaystyle\frac{ l }{ s } k_m $ |
ergibt sich:
| $ F_k =\displaystyle\frac{ E S }{ L } u $ |
ID:(3209, 0)
Spannung
Gleichung
Die Federkraft ($F_k$) ist eine Funktion, die von der Elastizitätsmodul ($E$), die Körper Sektion ($S$), die Verlängerung ($u$) und der Körperlänge ($L$) abhängt.
| $ F_k =\displaystyle\frac{ E S }{ L } u $ |
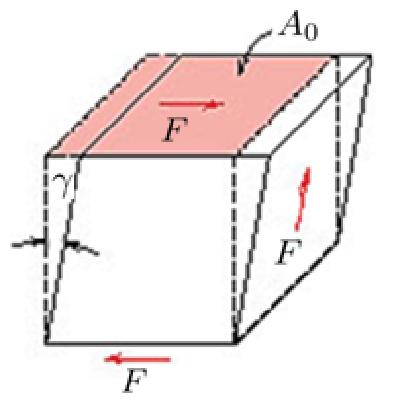
Ebenso, genau wie die Verformung ($\epsilon$) eingeführt wird, um die Verwendung der Dimension der Körperlänge ($L$) zu vermeiden, können wir einen Faktor konstruieren, der die Federkraft ($F_k$) in Abhängigkeit von die Körper Sektion ($S$) als die Spannung ($\sigma$) ausdrückt.
| $ \sigma =\displaystyle\frac{ F }{ S }$ |
ID:(3210, 0)
Poissonzahl
Gleichung
Die seitliche Verformung steht direkt im Verhältnis zur Verformung, die sie verursacht. Der Proportionalitätskoeffizient wird als der Poisson Koeffizient ($\nu$) [1] bezeichnet und liegt normalerweise im Bereich von 0,15 bis 0,4.
Wenn die ursprüngliche Verformung die Verformung ($\epsilon$) beträgt und die erzeugte Verformung die Verformung in Richtung senkrecht zur Kraft ($\epsilon_{\perp}$) ist, ergibt sich folgende Beziehung:
In der linearen Näherung repräsentiert der Poisson'sche Koeffizient das Verhältnis zwischen seitlichen und longitudinalen Verformungen.
| $ \epsilon_{\perp} =- \nu \epsilon $ |
wobei das Vorzeichen darauf hinweist, dass die Verformung in entgegengesetzter Richtung zur Ursache erfolgt.
[1] Dieses Konzept wurde von Siméon Denis Poisson in einer Arbeit zur statistischen Analyse eingeführt, in der er unter anderem Themen behandelt, die nichts mit Mechanik zu tun haben. Er erwähnt darin, was später als der Poisson'sche Koeffizient in einem Beispiel zur Elastizität bezeichnet wurde. Die Arbeit trägt den Titel "Recherches sur la Probabilité des Jugements en Matière Criminelle et en Matière Civile" (Forschungen zur Wahrscheinlichkeit von Urteilen in Straf- und Zivilsachen), verfasst von Siméon Denis Poisson (1837).
ID:(3765, 0)
Deformación elástica
Bild
Bajo pequeñas cargas el cuerpo se deforma sin que los átomos sufran desplazamientos relativos:
ID:(12889, 0)
Deformación plástica
Bild
Si se aumenta la deformación comienzan a ocurrir desplazamientos físicos de los átomos que modifican la estructura original:
ID:(12887, 0)
Tensión normal
Gleichung
La tensión normal se puede calcular de las tensiones en el eje vertical
| $ \sigma =\displaystyle\frac{1}{2}(( \sigma_1 + \sigma_3 ) + ( \sigma_1 - \sigma_3 )\cos 2 \theta )$ |
ID:(12884, 0)
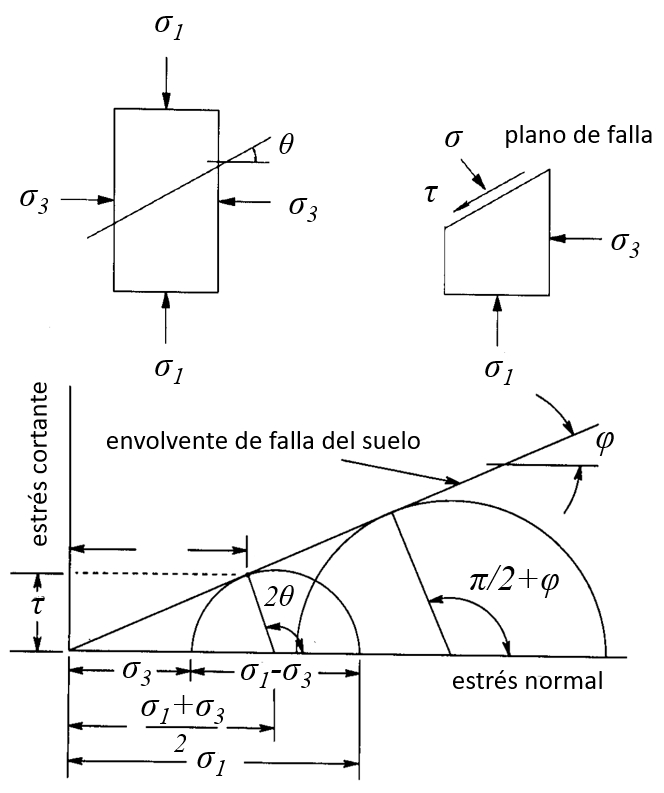
Limite de fractura de Mohr
Gleichung
La envolvente limite de Mohr se puede expresar como una ecuación de la forma
| $ \tau = \sigma_0 + \sigma \tan \phi $ |
con
ID:(12888, 0)
Fuerza de fricción
Gleichung
La fuerza de fricción se compone de
- La adhesión de la superficie $S$ del arado al suelo por efecto de la tensión superficial del agua contenida en este
- El roce por el desplazamiento que aumenta con la humedad por el efecto de aumento de la adhesión por efecto del agua. Pasado un cierto nivel vuelve a decrecer por el efecto lubricante de este.
La ecuación que lo representa se puede escribir como
| $ F = S \sigma_a + \mu F_N $ |
con
ID:(12885, 0)
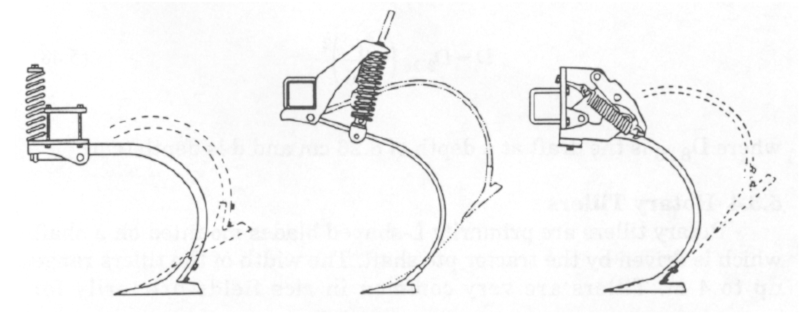
Coeficiente de fricción
Bild
La fuerza de fricción se compone de
- La adhesión de la superficie $S$ del arado al suelo por efecto de la tensión superficial del agua contenida en este
- El roce por el desplazamiento que aumenta con la humedad por el efecto de aumento de la adhesión por efecto del agua. Pasado un cierto nivel vuelve a decrecer por el efecto lubricante de este.
El coeficiente de roce varia con la humedad del suelo de la forma como se muestra
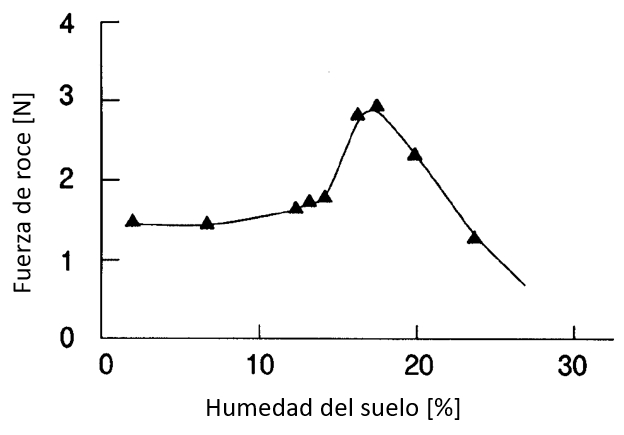
ID:(12886, 0)
