User:
Solar radiation
Storyboard 
The origin of the weather is the sun. Its energy reaches the earth by heating in a different way atmosphere and surface creating gradients that are balanced by conduction, convection and winds.
Therefore, the power of the sun must be studied, how it reaches the earth and how it is distributed over the earth's surface.
ID:(534, 0)
Mechanisms
Iframe
Mechanisms
ID:(15660, 0)
The sun
Description
The source of energy that defines the Earth's climate is the sun.
The key parameters of the sun are:
| Parameter | Variable | Value |
| Radius | $R$ | 696342 km |
| Surface Area | $S$ | 6.09E+12 km2 |
| Mass | $M$ | 1.98855E+30 kg |
| Density | $\rho$ | 1.408 g/cm2 |
| Surface Temperature | $T_s$ | 5778 K |
| Power | $P$ | 3.846E+26 W |
| Intensity | $I$ | 6.24E+7 W/m2 |
ID:(3078, 0)
Planet earth
Description
The planet Earth, shown in the following image:
has the following characteristics:
| Parameter | Symbol | Value |
| Distance from the sun | $r$ | 1.496E+8 km |
| Radius | $R$ | 6371.0 km |
| Mass | $M$ | 5.972E+24 kg |
| Orbit period | $T_o$ | 365 days |
| Rotation period | $T_r$ | 24 hours |
| Eccentricity | $\epsilon$ | 0.017 |
| Axis inclination | $\phi$ | 23.44° |
ID:(9990, 0)
The planets
Description
Below are the images of the different planets, in order: Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, Neptune, and Pluto:
The different planets have a variety of radii, masses, orbital and rotational periods, axial tilts, and distances from the sun, summarized as follows:
| Planet | Radius* | Mass* | Distance from Sun* | Orbital Period* | Rotation Period* | Eccentricity | Axial Tilt |
| Mercury | 0.382 | 0.06 | 0.39 | 0.24 | 58.64 | 0.206 | 0.04° |
| Venus | 0.949 | 0.82 | 0.72 | 0.62 | -243.02 | 0.007 | 177.36° |
| Earth | 1.000 | 1.00 | 1.00 | 1.00 | 1.00 | 0.017 | 23.44° |
| Mars | 0.532 | 0.11 | 1.52 | 1.88 | 1.03 | 0.093 | 25.19° |
| Jupiter | 11.209 | 317.8 | 5.2 | 11.86 | 0.41 | 0.048 | 3.13° |
| Saturn | 9.449 | 95.2 | 9.54 | 29.46 | 0.43 | 0.054 | 26.73° |
| Uranus | 4.007 | 14.6 | 19.22 | 84.01 | -0.72 | 0.047 | 97.77° |
| Neptune | 3.883 | 17.2 | 30.06 | 164.8 | 0.67 | 0.0009 | 28.32° |
| Pluto | 0.186 | 0.0022 | 39.482 | 247.94 | 1.005 | 0.2488 | 17.16° |
* data in proportion to Earth's value
ID:(9991, 0)
Intensity on the surface of the sun
Concept
The radiation intensity on the sun's surface ($I_s$) is defined as the sun power ($P_s$) per unit of the surface of the sun ($S_s$), where the power is represented by:
| $ I_s =\displaystyle\frac{ P_s }{ S_s }$ |
If we model the sun as a sphere with the sun Radio ($R_s$), its surface area is:
| $ S_s = 4 \pi R_s ^2$ |
Therefore, the radiation intensity on the sun's surface ($I_s$) is calculated as:
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
ID:(15655, 0)
Intensity of the sun in orbit
Concept
The intensity at orbit distance ($I_r$) is defined as the sun power ($P_s$) per unit of the sphere surface in orbit ($S_r$):
| $ I_r =\displaystyle\frac{ P_s }{ S_r }$ |
If we consider an imaginary sphere with a radius equal to the distance between the sun and the Earth, sphere surface in orbit ($S_r$), we can calculate its cross-sectional area:
| $ S_r = 4 \pi r ^2$ |
This allows us to obtain the intensity at orbit distance ($I_r$):
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
ID:(15657, 0)
Radius of the orbit of the earth and the sun
Description
The Sun's radiation propagates through its surface, which has an area of $4\pi R_s^2$ with a sun Radio ($R_s$) as the Sun's radius, and it is distributed at the distance of Earth's orbit, which has a surface area equal to $4\pi r^2$ with a distance earth sun ($r$) as the distance between the Earth and the Sun:
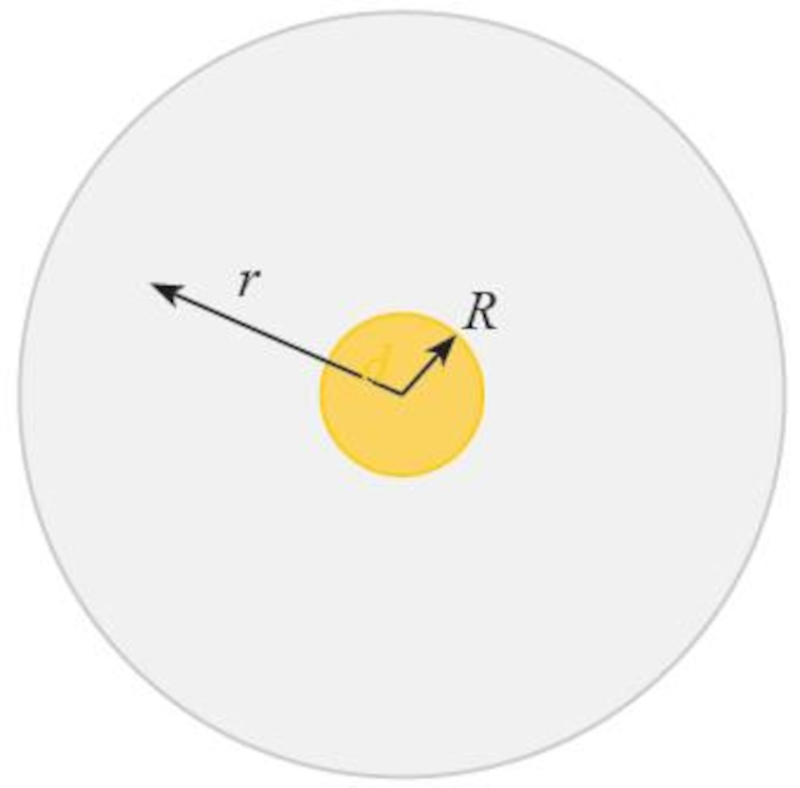
None
ID:(3082, 0)
Intensity in orbit relative to the sun
Concept
If we replace the sun power ($P_s$) of the sun, calculated as the radiation intensity on the sun's surface ($I_s$) on the surface of a sphere with a radius of sun Radio ($R_s$):
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
,
into the equation for the intensity at orbit distance ($I_r$) of sunlight at the distance earth sun ($r$):
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
,
we can obtain the relationship between intensities:
| $ I_r =\displaystyle\frac{ R_s ^2}{ r ^2} I_s $ |
ID:(15658, 0)
Power captured by the ground
Concept
Given that the intensity at orbit distance ($I_r$) reaching the Earth is equal to the power captured by the earth ($P_d$) captured by the section presenting the planet ($S_d$) according to:
| $ I_r =\displaystyle\frac{ P_d }{ S_d }$ |
and that the section presenting the planet ($S_d$) of the disk of the planet radius ($R_p$) is equal to:
| $ S_d = \pi R_p ^2$ |
,
we have:
| $ I_r =\displaystyle\frac{ P_d }{ \pi R_p ^2}$ |
.
ID:(15659, 0)
Area on earth that captures radiation
Description
The average earth intensity ($I_p$) over the entire surface of the planet radius ($R_p$) is equal to the intensity at orbit distance ($I_r$) captured by a disk of the planet radius ($R_p$), therefore:
$4\pi R_p^2 I_s = \pi R_p^2 I_p$
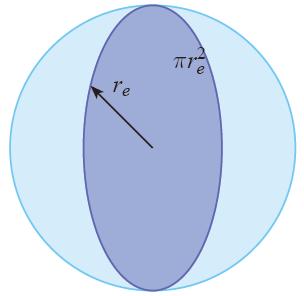
Therefore, it follows that:
| $ I_r =\displaystyle\frac{1}{4} I_p $ |
ID:(3084, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ I_s =\displaystyle\frac{ P_s }{ S_s }$
I = P / S
$ I_r =\displaystyle\frac{ P_s }{ S_r }$
I = P / S
$ I_r =\displaystyle\frac{ P_d }{ S_d }$
I = P / S
$ I_p =\displaystyle\frac{ P_d }{ S_p }$
I = P / S
$ I_r =\displaystyle\frac{ P_d }{ \pi R_p ^2}$
I = P /( pi * r ^2)
$ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$
I = P /(4* pi * r ^2)
$ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$
I = P /(4* pi * r ^2)
$ I_p = \displaystyle\frac{ P_d }{4 \pi R_p ^2}$
I = P /(4* pi * r ^2)
$ I_s =\displaystyle\frac{ R_s ^2}{ r ^2} I_r $
I_1 = ( r_2 ^2/ r_1 ^2)* I_2
$ I_r =\displaystyle\frac{1}{4} I_p $
I_r = I_p /4
$ S_s = 4 \pi R_s ^2$
S = 4* pi * r ^2
$ S_r = 4 \pi r ^2$
S = 4* pi * r ^2
$ S_p = 4 \pi R_p ^2$
S = 4* pi * r ^2
$ S_d = \pi R_p ^2$
S = pi * r ^2
ID:(15671, 0)
Intensity and power (1)
Equation
The intensity ($I$) is defined as the amount of the power ($P$) irradiated per unit of the surface of a sphere ($S$). Therefore, the following relationship is established:
| $ I_s =\displaystyle\frac{ P_s }{ S_s }$ |
| $ I =\displaystyle\frac{ P }{ S }$ |
ID:(9988, 1)
Intensity and power (2)
Equation
The intensity ($I$) is defined as the amount of the power ($P$) irradiated per unit of the surface of a sphere ($S$). Therefore, the following relationship is established:
| $ I_r =\displaystyle\frac{ P_s }{ S_r }$ |
| $ I =\displaystyle\frac{ P }{ S }$ |
ID:(9988, 2)
Intensity and power (3)
Equation
The intensity ($I$) is defined as the amount of the power ($P$) irradiated per unit of the surface of a sphere ($S$). Therefore, the following relationship is established:
| $ I_r =\displaystyle\frac{ P_d }{ S_d }$ |
| $ I =\displaystyle\frac{ P }{ S }$ |
ID:(9988, 3)
Intensity and power (4)
Equation
The intensity ($I$) is defined as the amount of the power ($P$) irradiated per unit of the surface of a sphere ($S$). Therefore, the following relationship is established:
| $ I_p =\displaystyle\frac{ P_d }{ S_p }$ |
| $ I =\displaystyle\frac{ P }{ S }$ |
ID:(9988, 4)
Surface of a sphere (1)
Equation
The surface of a sphere ($S$) of a radius of a sphere ($r$) can be calculated using the following formula:
| $ S_s = 4 \pi R_s ^2$ |
| $ S = 4 \pi r ^2$ |
ID:(4665, 1)
Surface of a sphere (2)
Equation
The surface of a sphere ($S$) of a radius of a sphere ($r$) can be calculated using the following formula:
| $ S_r = 4 \pi r ^2$ |
| $ S = 4 \pi r ^2$ |
ID:(4665, 2)
Surface of a sphere (3)
Equation
The surface of a sphere ($S$) of a radius of a sphere ($r$) can be calculated using the following formula:
| $ S_p = 4 \pi R_p ^2$ |
| $ S = 4 \pi r ^2$ |
ID:(4665, 3)
Intensity depending on power (1)
Equation
The intensity ($I$) is calculated as the power ($P$) divided by the surface area of a sphere with a radio ($r$):
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
The intensity ($I$) is defined as the power ($P$) per unit of the surface of a sphere ($S$):
| $ I =\displaystyle\frac{ P }{ S }$ |
If we consider an imaginary sphere with distance earth sun ($r$), we can calculate its surface:
| $ S = 4 \pi r ^2$ |
This allows us to obtain the intensity ($I$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
ID:(4662, 1)
Intensity depending on power (2)
Equation
The intensity ($I$) is calculated as the power ($P$) divided by the surface area of a sphere with a radio ($r$):
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
The intensity ($I$) is defined as the power ($P$) per unit of the surface of a sphere ($S$):
| $ I =\displaystyle\frac{ P }{ S }$ |
If we consider an imaginary sphere with distance earth sun ($r$), we can calculate its surface:
| $ S = 4 \pi r ^2$ |
This allows us to obtain the intensity ($I$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
ID:(4662, 2)
Intensity depending on power (3)
Equation
The intensity ($I$) is calculated as the power ($P$) divided by the surface area of a sphere with a radio ($r$):
| $ I_p = \displaystyle\frac{ P_d }{4 \pi R_p ^2}$ |
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
The intensity ($I$) is defined as the power ($P$) per unit of the surface of a sphere ($S$):
| $ I =\displaystyle\frac{ P }{ S }$ |
If we consider an imaginary sphere with distance earth sun ($r$), we can calculate its surface:
| $ S = 4 \pi r ^2$ |
This allows us to obtain the intensity ($I$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
ID:(4662, 3)
Surface of a disk
Equation
The surface of a disk ($S$) of ($$) is calculated as follows:
| $ S_d = \pi R_p ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 0)
Power captured
Equation
The intensity ($I$) is calculated by dividing the power ($P$) by the area of the disk with a radius of the radio ($r$), which means:
| $ I_r =\displaystyle\frac{ P_d }{ \pi R_p ^2}$ |
| $ I =\displaystyle\frac{ P }{ \pi r ^2}$ |
Given that the intensity ($I$) is the power ($P$) captured by the surface of a sphere ($S$) according to:
| $ I =\displaystyle\frac{ P }{ S }$ |
and that the surface of a disk ($S$) is the area of the disk of the disc radius ($r$), which is equal to:
| $ S_d = \pi R_p ^2$ |
,
we have:
| $ I =\displaystyle\frac{ P }{ \pi r ^2}$ |
.
ID:(4666, 0)
Intensity depending on solar intensity
Equation
The ratio between the intensity at orbit distance ($I_r$) and the radiation intensity on the sun's surface ($I_s$) is equal to the ratio of the surface area of a sphere with a radius of the sun Radio ($R_s$) to the surface area of a sphere with a radius of the distance earth sun ($r$), therefore it is:
| $ I_r =\displaystyle\frac{ R_s ^2}{ r ^2} I_s $ |
| $ I_1 =\displaystyle\frac{ r_2 ^2}{ r_1 ^2} I_2 $ |
If we replace the sun power ($P_s$) of the sun, calculated as the radiation intensity on the sun's surface ($I_s$) on the surface of a sphere with a radius of sun Radio ($R_s$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
,
into the equation for the intensity at orbit distance ($I_r$) of sunlight at the distance earth sun ($r$):
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
,
we can obtain the relationship between intensities:
| $ I_1 =\displaystyle\frac{ r_2 ^2}{ r_1 ^2} I_2 $ |
ID:(4663, 0)
Average intensity emitted by the earth
Equation
The average earth intensity ($I_p$) is equal to one-fourth of the intensity at orbit distance ($I_r$) because the surface area of the emitting sphere is four times larger than that of the capturing disk. Therefore:
| $ I_r =\displaystyle\frac{1}{4} I_p $ |
ID:(4667, 0)