Benützer:
Sonnenstrahlung
Storyboard 
Der Ursprung des Wetters ist die Sonne. Seine Energie erreicht die Erde, indem es auf eine andere Art und Weise die Atmosphäre und die Oberfläche erwärmt und dabei Steigungen erzeugt, die durch Wärmeleitung, Konvektion und Wind ausgeglichen werden.
Daher muss die Kraft der Sonne untersucht werden, wie sie auf die Erde gelangt und wie sie sich auf der Erdoberfläche verteilt.
ID:(534, 0)
Mechanismen
Iframe
Mechanismen
ID:(15660, 0)
Die Sonne
Beschreibung
Die Energiequelle, die das Klima auf der Erde bestimmt, ist die Sonne.
Die wichtigsten Parameter der Sonne sind:
| Parameter | Variable | Wert |
| Radius | $R$ | 696342 km |
| Oberfläche | $S$ | 6,09E+12 km2 |
| Masse | $M$ | 1,98855E+30 kg |
| Dichte | $\rho$ | 1,408 g/cm3 |
| Oberflächentemperatur | $T_s$ | 5778 K |
| Leistung | $P$ | 3,846E+26 W |
| Intensität | $I$ | 6,24E+7 W/m2 |
ID:(3078, 0)
Planet Erde
Beschreibung
Der Planet Erde, dargestellt im folgenden Bild:
hat die folgenden Eigenschaften:
| Parameter | Symbol | Wert |
| Entfernung zur Sonne | $r$ | 1.496E+8 km |
| Radius | $R$ | 6371.0 km |
| Masse | $M$ | 5.972E+24 kg |
| Umlaufdauer | $T_o$ | 365 Tage |
| Rotationszeitraum | $T_r$ | 24 Stunden |
| Exzentrizität | $\epsilon$ | 0,017 |
| Achsenneigung | $\phi$ | 23,44° |
ID:(9990, 0)
Die Planeten
Beschreibung
Unten sind die Bilder der verschiedenen Planeten in der Reihenfolge: Merkur, Venus, Erde, Mars, Jupiter, Saturn, Uranus, Neptun und Pluto:
Die verschiedenen Planeten haben unterschiedliche Radien, Massen, Umlauf- und Rotationsperioden, Achsneigungen und Entfernungen zur Sonne, die wie folgt zusammengefasst sind:
| Planet | Radius* | Masse* | Entfernung zur Sonne* | Umlaufperiode* | Rotationsperiode* | Exzentrizität | Achsneigung |
| Merkur | 0.382 | 0.06 | 0.39 | 0.24 | 58.64 | 0.206 | 0.04° |
| Venus | 0.949 | 0.82 | 0.72 | 0.62 | -243.02 | 0.007 | 177.36° |
| Erde | 1.000 | 1.00 | 1.00 | 1.00 | 1.00 | 0.017 | 23.44° |
| Mars | 0.532 | 0.11 | 1.52 | 1.88 | 1.03 | 0.093 | 25.19° |
| Jupiter | 11.209 | 317.8 | 5.2 | 11.86 | 0.41 | 0.048 | 3.13° |
| Saturn | 9.449 | 95.2 | 9.54 | 29.46 | 0.43 | 0.054 | 26.73° |
| Uranus | 4.007 | 14.6 | 19.22 | 84.01 | -0.72 | 0.047 | 97.77° |
| Neptun | 3.883 | 17.2 | 30.06 | 164.8 | 0.67 | 0.0009 | 28.32° |
| Pluto | 0.186 | 0.0022 | 39.482 | 247.94 | 1.005 | 0.2488 | 17.16° |
* Daten im Verhältnis zum Erdwert
ID:(9991, 0)
Intensität auf der Sonnenoberfläche
Konzept
Die Strahlungsintensität auf der Sonnenoberfläche ($I_s$)6493 wird als die Sonnenleistung ($P_s$)6494 pro Einheit von die Oberfläche der Sonne ($S_s$)6499 definiert, wobei die Leistung durch folgende Gleichung dargestellt wird:
| $ I_s =\displaystyle\frac{ P_s }{ S_s }$ |
Wenn wir die Sonne als eine Kugel mit einem Radius von der Solarradio ($R_s$)6492 modellieren, ist ihre Oberfläche:
| $ S_s = 4 \pi R_s ^2$ |
Daher wird die Strahlungsintensität auf der Sonnenoberfläche ($I_s$)6493 wie folgt berechnet:
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
ID:(15655, 0)
Intensität der Sonne im Orbit
Konzept
Die Intensität in Orbitentfernung ($I_r$)6495 wird als die Sonnenleistung ($P_s$)6494 pro Einheit von die Kugeloberfläche im Orbit ($S_r$)10360 definiert:
| $ I_r =\displaystyle\frac{ P_s }{ S_r }$ |
Wenn wir eine imaginäre Kugel mit einem Radius, der der Entfernung zwischen der Sonne und der Erde entspricht, Kugeloberfläche im Orbit ($S_r$)10360,0, betrachten, können wir deren Querschnittsfläche berechnen:
| $ S_r = 4 \pi r ^2$ |
Dies ermöglicht es uns, die Intensität in Orbitentfernung ($I_r$)6495 zu erhalten:
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
ID:(15657, 0)
Radius der Umlaufbahn von Erde und Sonne
Beschreibung
Die Strahlung der Sonne breitet sich über ihre Oberfläche aus, die eine Fläche von $4\pi R_s^2$ hat, wobei ein Solarradio ($R_s$)6492,1 der Radius der Sonne ist, und sie wird in der Entfernung der Erdumlaufbahn verteilt, die eine Fläche von $4\pi r^2$ hat, wobei eine Entfernung Erde Sun ($r$)6490,1 die Entfernung zwischen der Erde und der Sonne ist:
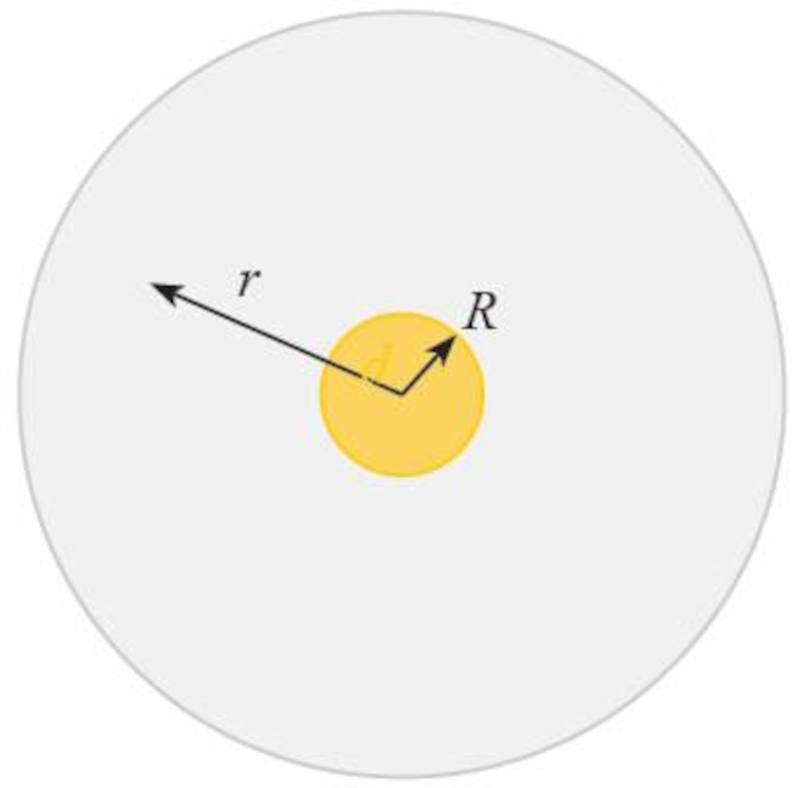
None
ID:(3082, 0)
Intensität im Orbit relativ zur Sonne
Konzept
Wenn wir die Sonnenleistung ($P_s$)6494 der Sonne, berechnet als die Strahlungsintensität auf der Sonnenoberfläche ($I_s$)6493 auf der Oberfläche einer Kugel mit einem Radius von Solarradio ($R_s$)6492,0:
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
,
in die Gleichung für die Intensität in Orbitentfernung ($I_r$)6495 der Sonnenstrahlung bei die Entfernung Erde Sun ($r$)6490 einsetzen:
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
,
können wir das Verhältnis der Intensitäten erhalten:
| $ I_r =\displaystyle\frac{ R_s ^2}{ r ^2} I_s $ |
ID:(15658, 0)
Vom Boden eingefangene Kraft
Konzept
Da die Intensität in Orbitentfernung ($I_r$)6495, das die Erde erreicht, gleich die Leistung von der Erde gefangen ($P_d$)6500 ist, das von die Abschnitt, der den Planeten vorstellt ($S_d$)6700 erfasst wird, gemäß:
| $ I_r =\displaystyle\frac{ P_d }{ S_d }$ |
und da die Abschnitt, der den Planeten vorstellt ($S_d$)6700 die Fläche der Scheibe von der Planetenradius ($R_p$)6501 ist, die gleich:
| $ S_d = \pi R_p ^2$ |
,
haben wir:
| $ I_r =\displaystyle\frac{ P_d }{ \pi R_p ^2}$ |
.
ID:(15659, 0)
Bereich auf der Erde, der Strahlung einfängt
Beschreibung
Die Durchschnittliche Intensität der Erde ($I_p$)6502 über die gesamte Oberfläche von der Planetenradius ($R_p$)6501 entspricht die Intensität in Orbitentfernung ($I_r$)6495, das von einer Scheibe von der Planetenradius ($R_p$)6501 erfasst wird, daher gilt:
$4\pi R_p^2 I_s = \pi R_p^2 I_p$
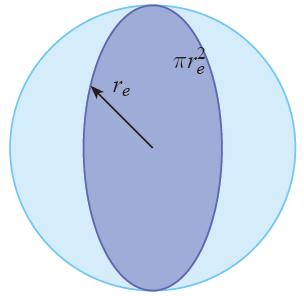
Daraus folgt:
| $ I_r =\displaystyle\frac{1}{4} I_p $ |
ID:(3084, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ I_s =\displaystyle\frac{ P_s }{ S_s }$
I = P / S
$ I_r =\displaystyle\frac{ P_s }{ S_r }$
I = P / S
$ I_r =\displaystyle\frac{ P_d }{ S_d }$
I = P / S
$ I_p =\displaystyle\frac{ P_d }{ S_p }$
I = P / S
$ I_r =\displaystyle\frac{ P_d }{ \pi R_p ^2}$
I = P /( pi * r ^2)
$ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$
I = P /(4* pi * r ^2)
$ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$
I = P /(4* pi * r ^2)
$ I_p = \displaystyle\frac{ P_d }{4 \pi R_p ^2}$
I = P /(4* pi * r ^2)
$ I_s =\displaystyle\frac{ R_s ^2}{ r ^2} I_r $
I_1 = ( r_2 ^2/ r_1 ^2)* I_2
$ I_r =\displaystyle\frac{1}{4} I_p $
I_r = I_p /4
$ S_s = 4 \pi R_s ^2$
S = 4* pi * r ^2
$ S_r = 4 \pi r ^2$
S = 4* pi * r ^2
$ S_p = 4 \pi R_p ^2$
S = 4* pi * r ^2
$ S_d = \pi R_p ^2$
S = pi * r ^2
ID:(15671, 0)
Intensität und Leistung (1)
Gleichung
Die Intensität ($I$)8391 wird als die Menge von die Leistung ($P$)6162 definiert, die pro Einheit von die Oberfläche einer Kugel ($S$)6551 abgestrahlt wird. Daher wird die folgende Beziehung etabliert:
| $ I_s =\displaystyle\frac{ P_s }{ S_s }$ |
| $ I =\displaystyle\frac{ P }{ S }$ |
ID:(9988, 1)
Intensität und Leistung (2)
Gleichung
Die Intensität ($I$)8391 wird als die Menge von die Leistung ($P$)6162 definiert, die pro Einheit von die Oberfläche einer Kugel ($S$)6551 abgestrahlt wird. Daher wird die folgende Beziehung etabliert:
| $ I_r =\displaystyle\frac{ P_s }{ S_r }$ |
| $ I =\displaystyle\frac{ P }{ S }$ |
ID:(9988, 2)
Intensität und Leistung (3)
Gleichung
Die Intensität ($I$)8391 wird als die Menge von die Leistung ($P$)6162 definiert, die pro Einheit von die Oberfläche einer Kugel ($S$)6551 abgestrahlt wird. Daher wird die folgende Beziehung etabliert:
| $ I_r =\displaystyle\frac{ P_d }{ S_d }$ |
| $ I =\displaystyle\frac{ P }{ S }$ |
ID:(9988, 3)
Intensität und Leistung (4)
Gleichung
Die Intensität ($I$)8391 wird als die Menge von die Leistung ($P$)6162 definiert, die pro Einheit von die Oberfläche einer Kugel ($S$)6551 abgestrahlt wird. Daher wird die folgende Beziehung etabliert:
| $ I_p =\displaystyle\frac{ P_d }{ S_p }$ |
| $ I =\displaystyle\frac{ P }{ S }$ |
ID:(9988, 4)
Oberfläche einer Kugel (1)
Gleichung
Die Oberfläche einer Kugel ($S$)6551 von ein Radius einer Kugel ($r$)10331,1 kann mit der folgenden Formel berechnet werden:
| $ S_s = 4 \pi R_s ^2$ |
| $ S = 4 \pi r ^2$ |
ID:(4665, 1)
Oberfläche einer Kugel (2)
Gleichung
Die Oberfläche einer Kugel ($S$)6551 von ein Radius einer Kugel ($r$)10331,1 kann mit der folgenden Formel berechnet werden:
| $ S_r = 4 \pi r ^2$ |
| $ S = 4 \pi r ^2$ |
ID:(4665, 2)
Oberfläche einer Kugel (3)
Gleichung
Die Oberfläche einer Kugel ($S$)6551 von ein Radius einer Kugel ($r$)10331,1 kann mit der folgenden Formel berechnet werden:
| $ S_p = 4 \pi R_p ^2$ |
| $ S = 4 \pi r ^2$ |
ID:(4665, 3)
Intensität je nach Leistung (1)
Gleichung
Die Intensität ($I$)8391 wird berechnet als die Leistung ($P$)6162 dividiert durch die Oberfläche einer Kugel mit ein Radio ($r$)10362,1:
| $ I_s = \displaystyle\frac{ P_s }{4 \pi R_s ^2}$ |
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
Die Intensität ($I$)8391 ist definiert als die Leistung ($P$)6162 pro Einheit von die Oberfläche einer Kugel ($S$)6551:
| $ I =\displaystyle\frac{ P }{ S }$ |
Wenn wir eine imaginäre Kugel mit Entfernung Erde Sun ($r$)6490,0 betrachten, können wir ihre Oberfläche berechnen:
| $ S = 4 \pi r ^2$ |
Dadurch können wir die Intensität ($I$)8391 erhalten:
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
ID:(4662, 1)
Intensität je nach Leistung (2)
Gleichung
Die Intensität ($I$)8391 wird berechnet als die Leistung ($P$)6162 dividiert durch die Oberfläche einer Kugel mit ein Radio ($r$)10362,1:
| $ I_r = \displaystyle\frac{ P_s }{4 \pi r ^2}$ |
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
Die Intensität ($I$)8391 ist definiert als die Leistung ($P$)6162 pro Einheit von die Oberfläche einer Kugel ($S$)6551:
| $ I =\displaystyle\frac{ P }{ S }$ |
Wenn wir eine imaginäre Kugel mit Entfernung Erde Sun ($r$)6490,0 betrachten, können wir ihre Oberfläche berechnen:
| $ S = 4 \pi r ^2$ |
Dadurch können wir die Intensität ($I$)8391 erhalten:
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
ID:(4662, 2)
Intensität je nach Leistung (3)
Gleichung
Die Intensität ($I$)8391 wird berechnet als die Leistung ($P$)6162 dividiert durch die Oberfläche einer Kugel mit ein Radio ($r$)10362,1:
| $ I_p = \displaystyle\frac{ P_d }{4 \pi R_p ^2}$ |
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
Die Intensität ($I$)8391 ist definiert als die Leistung ($P$)6162 pro Einheit von die Oberfläche einer Kugel ($S$)6551:
| $ I =\displaystyle\frac{ P }{ S }$ |
Wenn wir eine imaginäre Kugel mit Entfernung Erde Sun ($r$)6490,0 betrachten, können wir ihre Oberfläche berechnen:
| $ S = 4 \pi r ^2$ |
Dadurch können wir die Intensität ($I$)8391 erhalten:
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
ID:(4662, 3)
Oberfläche einer Scheibe
Gleichung
Die Oberfläche einer Scheibe ($S$)10361 von ein Scheibenradius ($r$)5275,1 wird wie folgt berechnet:
| $ S_d = \pi R_p ^2$ |
| $ S = \pi r ^2$ |
ID:(3804, 0)
Eingefangene Leistung
Gleichung
Die Intensität ($I$)8391 wird berechnet, indem die Leistung ($P$)6162 durch die Fläche der Scheibe mit einem Radius von der Radio ($r$)10362 dividiert wird, das heißt:
| $ I_r =\displaystyle\frac{ P_d }{ \pi R_p ^2}$ |
| $ I =\displaystyle\frac{ P }{ \pi r ^2}$ |
Da die Intensität ($I$)8391 Die Leistung ($P$)6162 ist, das von die Oberfläche einer Kugel ($S$)6551 erfasst wird, gemäß:
| $ I =\displaystyle\frac{ P }{ S }$ |
und die Oberfläche einer Scheibe ($S$)10361 die Fläche der Scheibe von der Scheibenradius ($r$)5275 ist, die gleich:
| $ S_d = \pi R_p ^2$ |
,
haben wir:
| $ I =\displaystyle\frac{ P }{ \pi r ^2}$ |
.
ID:(4666, 0)
Intensität abhängig von der Sonnenintensität
Gleichung
Das Verhältnis zwischen die Intensität in Orbitentfernung ($I_r$)6495 und die Strahlungsintensität auf der Sonnenoberfläche ($I_s$)6493 entspricht dem Verhältnis der Oberfläche einer Kugel mit einem Radius von der Solarradio ($R_s$)6492 zur Oberfläche einer Kugel mit einem Radius von die Entfernung Erde Sun ($r$)6490. Daher ist es:
| $ I_r =\displaystyle\frac{ R_s ^2}{ r ^2} I_s $ |
| $ I_1 =\displaystyle\frac{ r_2 ^2}{ r_1 ^2} I_2 $ |
Wenn wir die Sonnenleistung ($P_s$)6494 der Sonne, berechnet als die Strahlungsintensität auf der Sonnenoberfläche ($I_s$)6493 auf der Oberfläche einer Kugel mit einem Radius von Solarradio ($R_s$)6492,0:
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
,
in die Gleichung für die Intensität in Orbitentfernung ($I_r$)6495 der Sonnenstrahlung bei die Entfernung Erde Sun ($r$)6490 einsetzen:
| $ I = \displaystyle\frac{ P }{4 \pi r ^2}$ |
,
können wir das Verhältnis der Intensitäten erhalten:
| $ I_1 =\displaystyle\frac{ r_2 ^2}{ r_1 ^2} I_2 $ |
ID:(4663, 0)
Durchschnittliche von der Erde abgestrahlte Intensität
Gleichung
Die Durchschnittliche Intensität der Erde ($I_p$)6502 ist gleich ein Viertel von die Intensität in Orbitentfernung ($I_r$)6495, da die Oberfläche der emittierenden Kugel viermal größer ist als die des aufnehmenden Diskus. Daher:
| $ I_r =\displaystyle\frac{1}{4} I_p $ |
ID:(4667, 0)