Nova temperatura da atmosfera mais baixa
Equação 
A nova temperatura T_{bt} é calculada somando a temperatura inicial T_b com a variação \delta T_b:
ID:(7606, 0)
Nova temperatura da atmosfera superior
Equação 
A nova temperatura T_{tt} é calculada somando a temperatura inicial T_t com a variação \delta T_t:
ID:(7607, 0)
Nova temperatura da terra
Equação 
A nova temperatura T_{et} é calculada somando a temperatura inicial T_e com a variação \delta T_e:
ID:(7605, 0)
Fundamentos do modelo
Descrição 
Como os parâmetros do modelo variam pouco em torno de seus valores médios, é possível realizar um desenvolvimento de Taylor em torno dos valores médios. Dessa forma, obtemos equações lineares que podem ser resolvidas de forma exata.
ID:(84, 0)
Nova intensidade
Equação 
A nova intensidade I_{st} é calculada somando a intensidade inicial I_s com a variação \delta I_s:
ID:(7604, 0)
Modelo básico de fluxo radiativo
Imagem 
O seguinte diagrama ilustra os principais fluxos radiativos (visível e infravermelho) em um modelo simplificado da Terra:
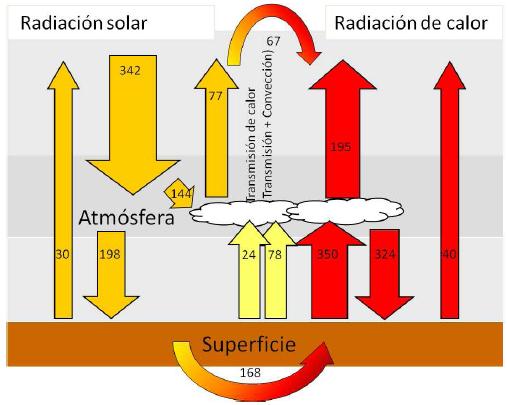
Este diagrama representa, de forma simplificada, a interação da radiação na Terra. A radiação visível do sol atinge a superfície terrestre, onde pode ser refletida de volta para o espaço, absorvida pela superfície terrestre e convertida em radiação infravermelha, ou absorvida pela atmosfera. Por sua vez, a Terra emite radiação infravermelha para o espaço.
Esses fluxos radiativos são fundamentais para entender o equilíbrio energético de nosso planeta e os processos que regulam o clima.
ID:(7331, 0)
Assunção evolução da sociedade
Descrição 
Para simular o desenvolvimento futuro do clima, foram assumidos quatro possíveis cenários:
- A1: Crescimento econômico rápido, triplicação do consumo de energia até 2100. Aumento da população para 9 bilhões em 2050 e posterior diminuição lenta.
- A2: Crescimento econômico pontual, inicialmente consumo de energia lento, mas triplicação até 2100. Aumento contínuo da população até 15 bilhões em 2100.
- B1: Crescimento econômico rápido, diminuição do consumo de energia até 2100. Aumento da população para 9 bilhões em 2050 e posterior diminuição lenta.
- B2: Crescimento econômico mais lento, forte aumento inicial do consumo de energia, mas estabilização até 2100. Aumento da população lento até 10 bilhões em 2100.
Em cada um desses cenários, estima-se com base em:
- Consumo de energia e forma como é gerada.
- Produção e tipo de alimentos consumidos.
E estima-se a geração dos gases correspondentes.
ID:(7324, 0)
Equações de equilíbrio
Descrição 
No caso de equilíbrio, as seguintes três equações de equilíbrio radiativo são válidas:
(1 - a_a)(1 - \gamma_{\nu})I_s - \kappa (T_e - T_b) - \sigma\epsilon_eT_e^4 + \sigma\epsilon_b T_b^4 = 0
\kappa(T_e - T_b) + \gamma_i\sigma\epsilon_e T_e^4 - 2\sigma\epsilon_bT_b^4 = 0
(1 - a_a)\gamma_{\nu} + \sigma\epsilon_b T_b^4 - 2\sigma\epsilon_t T_t^4 = 0
onde T_e é a temperatura da Terra, T_b é a temperatura na parte inferior da atmosfera e T_t é a temperatura na parte superior. Além disso, temos a radiação solar média I_s, os albedos da atmosfera e da Terra denotados por a_a e a_e respectivamente, $\gamma_{
u} e \gamma_i representam os fatores de cobertura no espectro visível e infravermelho, \epsilon_e e \epsilon_a representam a emissividade da Terra e da atmosfera, e \sigma$ é a constante de Stefan-Boltzmann.
ID:(85, 0)
Equações de equilíbrio
Descrição 
Usando as aproximações, obtemos para a equação que, em uma aproximação linear, é:
-\kappa(\delta T_e-\delta T_b)-4\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_b T_b^3\delta T_b-\delta a_e(1-\gamma_{\nu})I_s-(1-a_e)\delta\gamma_{\nu}I_s=0
Da mesma forma, para a segunda equação, temos:
\kappa(\delta T_e-\delta T_b)+\sigma\epsilon_e T_e^4\delta\gamma_i+4\gamma_i\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_t T_t^3\delta T_t-8\sigma\epsilon_b T_b^3\delta T_b=0
E para a terceira equação:
-2\sigma \epsilon_t T_t^3\delta T_t+\sigma\epsilon_b T_b^3\delta T_b-\gamma_{\nu}I_s\delta a_a+(1-a_a) I_s\delta\gamma_i=0
Essas três equações formam um sistema de equações lineares para calcular as variações das temperaturas \delta T_e, \delta T_b e \delta T_t em termos das variações dos albedos \delta a_e e \delta a_a, e dos fatores de cobertura $\delta \gamma_{
u} e \delta \gamma_i$.
ID:(87, 0)
Simulador de modelo
Descrição 
As equações de balanço radiativo nos permitem calcular as temperaturas na superfície da Terra T_e, na parte inferior da atmosfera T_b e na parte superior T_t. Essas equações são representadas da seguinte forma:
Equação 1: A mudança na temperatura na superfície da Terra é calculada usando a equação:
M_eC_e\displaystyle\frac{dT_e}{dt}=(1-a_e)(1-\gamma_v)I_s-\kappa(T_e-T_b)-\sigma\epsilon T_e^4+\sigma\epsilon T_b^4
onde M_e é a massa da Terra, C_e é a capacidade térmica da Terra, a_e é o albedo da Terra, \gamma_v é a fração de radiação visível absorvida pela atmosfera, I_s é a radiação solar incidente, \kappa é a condutividade térmica, \sigma é a constante de Stefan-Boltzmann e \epsilon é a emissividade da Terra.
Equação 2: A mudança na temperatura na parte inferior da atmosfera é calculada usando a equação:
M_bC_b\displaystyle\frac{dT_b}{dt}=\kappa(T_e-T_b)+\gamma_i\sigma\epsilon T_e^4-2\sigma\epsilon T_b^4+\sigma\epsilon T_t^4=0
onde M_b é a massa da atmosfera, C_b é a capacidade térmica da atmosfera e \gamma_i é a fração de radiação infravermelha absorvida pela atmosfera.
Equação 3: A mudança na temperatura na parte superior da atmosfera é calculada usando a equação:
M_tC_t\displaystyle\frac{dT_t}{dt}=(1-a_a)\gamma_vI_s+\sigma\epsilon T_b^4-2\sigma\epsilon T_t^4=0
onde M_t é a massa da parte superior da atmosfera e C_t é a capacidade térmica da parte superior da atmosfera.
Essas equações representam o equilíbrio entre a radiação solar incidente, a radiação emitida pela Terra e a radiação transferida entre diferentes camadas da Terra e da atmosfera. Ao resolver essas equações, podemos obter as temperaturas em cada uma dessas camadas.
ID:(6867, 0)
Solução numérica
Descrição 
O sistema de equações pode ser resolvido analiticamente. Se avaliarmos as expressões para os parâmetros da condição atual da Terra (a_e = 0.152, a_a = 0.535, \gamma_{ u} = 0.421, \gamma_i=0.897, \kappa = 2.226 , \text{W/m}^2\text{K}^{-1}, \epsilon_e = \epsilon_b = \epsilon_t = 1, I_s = 342 , \text{W/m}^2, T_e = 14.8^\circ \text{C}, T_b = 1.79^\circ \text{C} e T_t = -30.98^\circ \text{C}), obteremos:
ID:(7319, 0)
