Nouvelle température de la haute atmosphère
Équation 
La nouvelle température T_{tt} est calculée en ajoutant la température initiale T_t à la variation $\delta T_t:
ID:(7607, 0)
Nouvelle température de la terre
Équation 
La nouvelle température T_{et} est calculée en ajoutant la température initiale T_e à la variation \delta T_e :
ID:(7605, 0)
Nouvelle température de l\'atmosphère inférieure
Équation 
La nouvelle température T_{bt} est calculée en ajoutant la température initiale T_b à la variation $\delta T_b:
ID:(7606, 0)
Fondamentaux du modèle
Description 
Étant donné que les paramètres du modèle varient peu autour de leurs valeurs moyennes, il est possible d\'effectuer un développement de Taylor autour de ces valeurs moyennes. Cela permet d\'obtenir des équations linéaires qui peuvent être résolues de manière exacte.
ID:(84, 0)
Nouvelle intensité
Équation 
La nouvelle intensité I_{st} est calculée en ajoutant l\'intensité initiale I_s à la variation \delta I_s:
ID:(7604, 0)
Modèle de base du flux radiatif
Image 
Le diagramme suivant illustre les principaux flux radiatifs (visible et infrarouge) dans un modèle simplifié de la Terre :
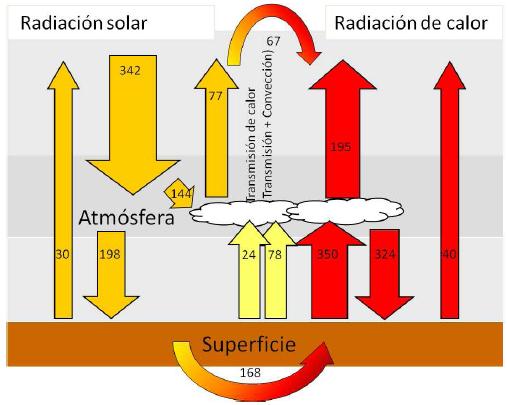
Ce diagramme représente de manière simplifiée l\'interaction des radiations sur Terre. Les radiations visibles du soleil atteignent la surface de la Terre, où elles peuvent être réfléchies vers l\'espace, absorbées par la surface terrestre et converties en rayonnement infrarouge, ou absorbées par l\'atmosphère. À son tour, la Terre émet un rayonnement infrarouge vers l\'espace.
Ces flux radiatifs sont fondamentaux pour comprendre l\'équilibre énergétique de notre planète et les processus qui régulent le climat.
ID:(7331, 0)
Hypothèse évolution de la société
Description 
Pour simuler le développement futur du climat, quatre scénarios possibles ont été envisagés :
- A1 : Croissance économique rapide, la consommation d\'énergie est multipliée par trois d\'ici 2100. Augmentation de la population à 9 milliards d\'ici 2050, suivie d\'un déclin lent.
- A2 : Croissance économique modérée, la consommation d\'énergie augmente progressivement mais est multipliée par trois d\'ici 2100. Augmentation continue de la population à 15 milliards d\'ici 2100.
- B1 : Croissance économique rapide, la consommation d\'énergie diminue d\'ici 2100. Augmentation de la population à 9 milliards d\'ici 2050, suivie d\'un déclin lent.
- B2 : Croissance économique plus lente, la consommation d\'énergie augmente de manière significative mais se stabilise d\'ici 2100. Augmentation lente de la population à 10 milliards d\'ici 2100.
Pour chacun de ces scénarios, on estime :
- La consommation d\'énergie et la manière dont elle est produite.
- La production et le type d\'aliments consommés.
De plus, la génération des gaz correspondants est estimée.
ID:(7324, 0)
Équations d\'équilibre
Description 
En cas d\'équilibre, les trois équations d\'équilibre radiatif suivantes sont satisfaites :
(1 - a_a)(1 - \gamma_{\nu})I_s - \kappa (T_e - T_b) - \sigma\epsilon_eT_e^4 + \sigma\epsilon_b T_b^4 = 0
\kappa(T_e - T_b) + \gamma_i\sigma\epsilon_e T_e^4 - 2\sigma\epsilon_bT_b^4 = 0
(1 - a_a)\gamma_{\nu} + \sigma\epsilon_b T_b^4 - 2\sigma\epsilon_t T_t^4 = 0
où T_e est la température de la Terre, T_b est la température de la basse atmosphère et T_t est la température de la haute atmosphère. De plus, nous avons le rayonnement solaire moyen I_s, les albédos de l\'atmosphère et de la Terre désignés par a_a et a_e respectivement, $\gamma_{
u} et \gamma_i représentent les facteurs de couverture dans le domaine visible et infrarouge, \epsilon_e et \epsilon_a représentent l\'émissivité de la Terre et de l\'atmosphère, et \sigma$ est la constante de Stefan-Boltzmann.
ID:(85, 0)
Équations d\'équilibre
Description 
En utilisant les approximations, on obtient pour l\'équation qui, dans une approximation linéaire, est :
-\kappa(\delta T_e-\delta T_b)-4\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_b T_b^3\delta T_b-\delta a_e(1-\gamma_{\nu})I_s-(1-a_e)\delta\gamma_{\nu}I_s=0
De même, pour la deuxième équation, on a :
\kappa(\delta T_e-\delta T_b)+\sigma\epsilon_e T_e^4\delta\gamma_i+4\gamma_i\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_t T_t^3\delta T_t-8\sigma\epsilon_b T_b^3\delta T_b=0
Et pour la troisième équation :
-2\sigma \epsilon_t T_t^3\delta T_t+\sigma\epsilon_b T_b^3\delta T_b-\gamma_{\nu}I_s\delta a_a+(1-a_a) I_s\delta\gamma_i=0
Ces trois équations forment un système d\'équations linéaires pour calculer les variations des températures \delta T_e, \delta T_b et \delta T_t en fonction des variations des albédos \delta a_e et \delta a_a, et des facteurs de couverture $\delta \gamma_{
u} et \delta \gamma_i$.
ID:(87, 0)
Simulateur de modèle
Description 
Les équations de bilan radiatif nous permettent de calculer les températures à la surface de la Terre T_e, dans la basse atmosphère T_b et en haut T_t. Ces équations sont représentées de la manière suivante :
Équation 1 : Le changement de température à la surface de la Terre est calculé à l\'aide de l\'équation :
M_eC_e\displaystyle\frac{dT_e}{dt}=(1-a_e)(1-\gamma_v)I_s-\kappa(T_e-T_b)-\sigma\epsilon T_e^4+\sigma\epsilon T_b^4
où M_e est la masse de la Terre, C_e est la capacité thermique de la Terre, a_e est l\'albédo de la Terre, \gamma_v est la fraction de rayonnement visible absorbée par l\'atmosphère, I_s est le rayonnement solaire incident, \kappa est la conductivité thermique, \sigma est la constante de Stefan-Boltzmann et \epsilon est l\'émissivité de la Terre.
Équation 2 : Le changement de température dans la basse atmosphère est calculé à l\'aide de l\'équation :
M_bC_b\displaystyle\frac{dT_b}{dt}=\kappa(T_e-T_b)+\gamma_i\sigma\epsilon T_e^4-2\sigma\epsilon T_b^4+\sigma\epsilon T_t^4=0
où M_b est la masse de l\'atmosphère, C_b est la capacité thermique de l\'atmosphère et \gamma_i est la fraction de rayonnement infrarouge absorbée par l\'atmosphère.
Équation 3 : Le changement de température en haut de l\'atmosphère est calculé à l\'aide de l\'équation :
M_tC_t\displaystyle\frac{dT_t}{dt}=(1-a_a)\gamma_vI_s+\sigma\epsilon T_b^4-2\sigma\epsilon T_t^4=0
où M_t est la masse de la partie supérieure de l\'atmosphère et C_t est la capacité thermique de la partie supérieure de l\'atmosphère.
Ces équations représentent l\'équilibre entre le rayonnement solaire incident, le rayonnement émis par la Terre et le rayonnement transféré entre les différentes couches de la Terre et de l\'atmosphère. En résolvant ces équations, nous pouvons obtenir les températures dans chacune de ces couches.
ID:(6867, 0)
Solution numérique
Description 
Le système d\'équations peut être résolu analytiquement. Si nous évaluons les expressions pour les paramètres de l\'état actuel de la Terre (a_e = 0.152, a_a = 0.535, \gamma_{ u} = 0.421, \gamma_i=0.897, \kappa = 2.226 , \text{W/m}^2\text{K}^{-1}, \epsilon_e = \epsilon_b = \epsilon_t = 1, I_s = 342 , \text{W/m}^2, T_e = 14.8^\circ \text{C}, T_b = 1.79^\circ \text{C} et T_t = -30.98^\circ \text{C}), nous aurons :
ID:(7319, 0)
