Storyboard

Die Gleichungen für die Temperatur der Erdoberfläche, des Erdbodens und der Erdoberfläche können durch Störungstechniken gelöst werden. Dies setzt geringe Schwankungen der Sonnenintensität, der Albedos und der Bedeckungsfaktoren voraus und es wird geschätzt, wie sich diese auf die Schwankungen dieser Temperaturen auswirken.

>Modell

ID:(575, 0)

Gleichung

>Top, >Modell

Die neue Temperatur $T_{et}$ wird berechnet, indem die Anfangstemperatur $T_e$ mit der Änderung $\delta T_e$ addiert wird:

$ T_{et} = T_e + \delta T_e $

Bedingungen

Variablen

$T_{et}$

Nueva Temperatura terrestre

$K$

7609

$T_e$

Temperatur der Planetenoberfläche

$K$

7448

$\delta T_e$

Variación de la Temperatura terrestre ($\delta T_e)

$K$

7443

Beziehung

ID:(7605, 0)

Gleichung

>Top, >Modell

Die neue Temperatur $T_{bt}$ wird berechnet, indem die Anfangstemperatur $T_b$ mit der Änderung $\delta T_b$ addiert wird:

$ T_{bt} = T_b + \delta T_b $

Bedingungen

Variablen

$T_{bt}$

Nueva Temperatura atmosferica inferior

$K$

7611

$T_b$

Temperatura atmosferica inferior ($T_b$)

$K$

7446

$\delta T_b$

Variación de la Temperatura atmosferica inferior ($\delta T_b)

$K$

7444

Beziehung

ID:(7606, 0)

Gleichung

>Top, >Modell

Die neue Temperatur $T_{tt}$ wird berechnet, indem die Anfangstemperatur $T_t$ mit der Änderung $\delta T_t$ addiert wird:

$ T_{tt} = T_t + \delta T_t $

Bedingungen

Variablen

$T_{tt}$

Nueva Temperatura atmosferica superior

$K$

7610

$T_t$

Temperatur in der oberen Atmosphäre

$K$

7447

$\delta T_t$

Variación de la Temperatura atmosferica superior ($\delta T_t)

$K$

7445

Beziehung

ID:(7607, 0)

Beschreibung

>Top

Da die Parameter des Modells nur geringfügig um ihre Mittelwerte variieren, kann um die Mittelwerte herum eine Taylor-Entwicklung durchgeführt werden. Dadurch ergeben sich lineare Gleichungen, die exakt gelöst werden können.

ID:(84, 0)

Gleichung

>Top, >Modell

Die neue Intensität $I_{st}$ wird berechnet, indem die anfängliche Intensität $I_s$ mit der Variation $\delta I_s$ addiert wird:

$ I_{st} = I_s + \delta I_s $

Bedingungen

Variablen

$I_s$

Intensidad de Radiación Solar

$W/m^2$

7449

$I_{st}$

Nueva Intensidad de Radiación Solar

$W/m^2$

7608

$\delta I_s$

Variación de Intensidad de Radiación Solar

$W/m^2$

7450

Beziehung

ID:(7604, 0)

Bild

>Top

Das folgende Diagramm veranschaulicht die Hauptstrahlungsflüsse (sichtbar und infrarot) in einem vereinfachten Modell der Erde:

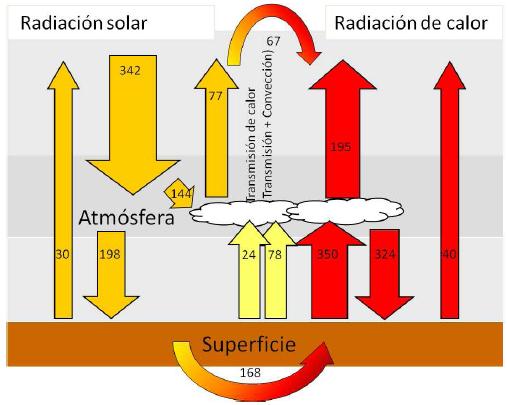
Dieses Diagramm stellt vereinfacht die Wechselwirkung von Strahlung auf der Erde dar. Sichtbare Strahlung von der Sonne erreicht die Erdoberfläche, wo sie entweder zurück ins All reflektiert, von der Erdoberfläche absorbiert und in Infrarotstrahlung umgewandelt oder von der Atmosphäre absorbiert wird. Gleichzeitig gibt die Erde Infrarotstrahlung in den Weltraum ab.

Diese Strahlungsflüsse sind entscheidend, um das Energiegleichgewicht unseres Planeten und die Prozesse, die das Klima regulieren, zu verstehen.

ID:(7331, 0)

Beschreibung

>Top

Um die zukünftige Entwicklung des Klimas zu simulieren, wurden vier mögliche Szenarien angenommen:

- A1: Schnelles wirtschaftliches Wachstum, der Energieverbrauch verdreifacht sich bis zum Jahr 2100. Bevölkerungszuwachs auf 9 Milliarden bis 2050 und anschließender langsamer Rückgang.

- A2: Moderate wirtschaftliche Entwicklung, der Energieverbrauch steigt allmählich an, verdreifacht sich jedoch bis zum Jahr 2100. Kontinuierlicher Bevölkerungszuwachs auf 15 Milliarden bis 2100.

- B1: Schnelles wirtschaftliches Wachstum, der Energieverbrauch nimmt bis zum Jahr 2100 ab. Bevölkerungszuwachs auf 9 Milliarden bis 2050 und anschließender langsamer Rückgang.

- B2: Langsames wirtschaftliches Wachstum, der Energieverbrauch steigt deutlich an, stabilisiert sich jedoch bis zum Jahr 2100. Langsamer Bevölkerungszuwachs auf 10 Milliarden bis 2100.

Für jedes dieser Szenarien wird Folgendes geschätzt:

- Der Energieverbrauch und die Art und Weise, wie sie erzeugt wird.

- Die Produktion und Art der konsumierten Lebensmittel.

Darüber hinaus wird die Entstehung der entsprechenden Gase geschätzt.

ID:(7324, 0)

Beschreibung

>Top

Im Fall des Gleichgewichts gelten die folgenden drei Strahlungsgleichgewichtsgleichungen:

$(1 - a_a)(1 - \gamma_{\nu})I_s - \kappa (T_e - T_b) - \sigma\epsilon_eT_e^4 + \sigma\epsilon_b T_b^4 = 0$

$\kappa(T_e - T_b) + \gamma_i\sigma\epsilon_e T_e^4 - 2\sigma\epsilon_bT_b^4 = 0$

$(1 - a_a)\gamma_{\nu} + \sigma\epsilon_b T_b^4 - 2\sigma\epsilon_t T_t^4 = 0$

Dabei ist $T_e$ die Temperatur der Erde, $T_b$ die Temperatur in der unteren Atmosphäre und $T_t$ die Temperatur in der oberen Atmosphäre. Zusätzlich haben wir die durchschnittliche solare Strahlung $I_s$, die Albedo-Werte der Atmosphäre und der Erde, bezeichnet als $a_a$ und $a_e$ respectively, $\gamma_{

u}$ und $\gamma_i$ repräsentieren die Abdeckungsfaktoren im sichtbaren und infraroten Bereich, $\epsilon_e$ und $\epsilon_a$ repräsentieren die Emissionsfähigkeit der Erde und der Atmosphäre, und $\sigma$ ist die Stefan-Boltzmann-Konstante.

ID:(85, 0)

Beschreibung

>Top

Unter Verwendung der Näherungen ergibt sich für die Gleichung in einer linearen Approximation:

$-\kappa(\delta T_e-\delta T_b)-4\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_b T_b^3\delta T_b-\delta a_e(1-\gamma_{\nu})I_s-(1-a_e)\delta\gamma_{\nu}I_s=0$

Ähnlich erhält man für die zweite Gleichung:

$\kappa(\delta T_e-\delta T_b)+\sigma\epsilon_e T_e^4\delta\gamma_i+4\gamma_i\sigma\epsilon_e T_e^3\delta T_e+4\sigma\epsilon_t T_t^3\delta T_t-8\sigma\epsilon_b T_b^3\delta T_b=0$

Und für die dritte Gleichung:

$-2\sigma \epsilon_t T_t^3\delta T_t+\sigma\epsilon_b T_b^3\delta T_b-\gamma_{\nu}I_s\delta a_a+(1-a_a) I_s\delta\gamma_i=0$

Diese drei Gleichungen bilden ein System linearer Gleichungen, um die Variationen der Temperaturen $\delta T_e$, $\delta T_b$ und $\delta T_t$ in Abhängigkeit von den Variationen der Albedos $\delta a_e$ und $\delta a_a$ und der Deckungsfaktoren $\delta \gamma_{

u}$ und $\delta \gamma_i$ zu berechnen.

ID:(87, 0)

Beschreibung

>Top

Die Strahlungsbilanzgleichungen ermöglichen es uns, die Temperaturen an der Erdoberfläche $T_e$, in der unteren Atmosphäre $T_b$ und an der Spitze $T_t$ zu berechnen. Diese Gleichungen werden wie folgt dargestellt:

Gleichung 1: Die Änderung der Temperatur an der Erdoberfläche wird mit folgender Gleichung berechnet:

$M_eC_e\displaystyle\frac{dT_e}{dt}=(1-a_e)(1-\gamma_v)I_s-\kappa(T_e-T_b)-\sigma\epsilon T_e^4+\sigma\epsilon T_b^4$

Dabei ist $M_e$ die Masse der Erde, $C_e$ die Wärmekapazität der Erde, $a_e$ das Albedo der Erde, $\gamma_v$ der Anteil der von der Atmosphäre absorbierten sichtbaren Strahlung, $I_s$ die einfallende Sonnenstrahlung, $\kappa$ die Wärmeleitfähigkeit, $\sigma$ die Stefan-Boltzmann-Konstante und $\epsilon$ die Emissionsfähigkeit der Erde.

Gleichung 2: Die Änderung der Temperatur in der unteren Atmosphäre wird mit folgender Gleichung berechnet:

$M_bC_b\displaystyle\frac{dT_b}{dt}=\kappa(T_e-T_b)+\gamma_i\sigma\epsilon T_e^4-2\sigma\epsilon T_b^4+\sigma\epsilon T_t^4=0$

Dabei ist $M_b$ die Masse der Atmosphäre, $C_b$ die Wärmekapazität der Atmosphäre und $\gamma_i$ der Anteil der von der Atmosphäre absorbierten Infrarotstrahlung.

Gleichung 3: Die Änderung der Temperatur an der Spitze der Atmosphäre wird mit folgender Gleichung berechnet:

$M_tC_t\displaystyle\frac{dT_t}{dt}=(1-a_a)\gamma_vI_s+\sigma\epsilon T_b^4-2\sigma\epsilon T_t^4=0$

Dabei ist $M_t$ die Masse der oberen Atmosphäre und $C_t$ die Wärmekapazität der oberen Atmosphäre.

Diese Gleichungen repräsentieren das Gleichgewicht zwischen der einfallenden Sonnenstrahlung, der von der Erde abgegebenen Strahlung und der zwischen verschiedenen Schichten der Erde und der Atmosphäre übertragenen Strahlung. Durch Lösung dieser Gleichungen können wir die Temperaturen in jeder dieser Schichten bestimmen.

ID:(6867, 0)

Beschreibung

>Top

Das Gleichungssystem kann analytisch gelöst werden. Wenn wir die Ausdrücke für die Parameter des aktuellen Zustands der Erde ($a_e = 0.152$, $a_a = 0.535$, $\gamma_{
u} = 0.421$, $\gamma_i=0.897$, $\kappa = 2.226 , \text{W/m}^2\text{K}^{-1}$, $\epsilon_e = \epsilon_b = \epsilon_t = 1$, $I_s = 342 , \text{W/m}^2$, $T_e = 14.8^\circ \text{C}$, $T_b = 1.79^\circ \text{C}$ und $T_t = -30.98^\circ \text{C}$) auswerten, erhalten wir:

ID:(7319, 0)

Gleichung

>Top, >Modell

La temperatura terrestre se puede estimar mediante:

$\delta T_e = 0.240\delta I_s - 97.978\delta\gamma_{

u}+123.671\delta \gamma_i - 84.112\delta a_e - 22.827\delta a_a$

$\delta T_b = 0.193\delta I_s - 66.120\delta \gamma_{

u} + 136.209\delta \gamma_i - 64.106\delta a_e - 25.142\delta a_a$

$\delta T_t = 0.172\delta I_s - 23.693\delta \gamma_{

u} + 99.662\delta \gamma_i-46.905\delta a_e - 40.745\delta a_a$

donde se asumieron los valores

Parámetros | Valor

-------------------|:---------:

$a_e$ | $0.152$

$a_a$ | $0.535$

$\gamma_{

u}$ | $0.421$

$\gamma_i$ | $0.897$

$\kappa$ | $2.226W/m^2K$

$\epsilon_e$ | $1$

$\epsilon_b$ | $1$

$\epsilon_t$ | $1$

$I_s$ | $342W/m^2$

$T_e$ | $14.8^{\circ}C$

$T_b$ | $1.79^{\circ}C$

$T_t$ | $-30.98^{\circ}C$

ID:(7440, 0)

Gleichung

>Top, >Modell

La temperatura terrestre se puede estimar mediante:

$\delta T_e = 0.240\delta I_s - 97.978\delta\gamma_{

u}+123.671\delta \gamma_i - 84.112\delta a_e - 22.827\delta a_a$

$\delta T_b = 0.193\delta I_s - 66.120\delta \gamma_{

u} + 136.209\delta \gamma_i - 64.106\delta a_e - 25.142\delta a_a$

$\delta T_t = 0.172\delta I_s - 23.693\delta \gamma_{

u} + 99.662\delta \gamma_i-46.905\delta a_e - 40.745\delta a_a$

donde se asumieron los valores

Parámetros | Valor

-------------------|:---------:

$a_e$ | $0.152$

$a_a$ | $0.535$

$\gamma_{

u}$ | $0.421$

$\gamma_i$ | $0.897$

$\kappa$ | $2.226W/m^2K$

$\epsilon_e$ | $1$

$\epsilon_b$ | $1$

$\epsilon_t$ | $1$

$I_s$ | $342W/m^2$

$T_e$ | $14.8^{\circ}C$

$T_b$ | $1.79^{\circ}C$

$T_t$ | $-30.98^{\circ}C$

ID:(7441, 0)

Gleichung

>Top, >Modell

La temperatura terrestre se puede estimar mediante:

$\delta T_e = 0.240\delta I_s - 97.978\delta\gamma_{

u}+123.671\delta \gamma_i - 84.112\delta a_e - 22.827\delta a_a$

$\delta T_b = 0.193\delta I_s - 66.120\delta \gamma_{

u} + 136.209\delta \gamma_i - 64.106\delta a_e - 25.142\delta a_a$

$\delta T_t = 0.172\delta I_s - 23.693\delta \gamma_{

u} + 99.662\delta \gamma_i-46.905\delta a_e - 40.745\delta a_a$

donde se asumieron los valores

Parámetros | Valor

-------------------|:---------:

$a_e$ | $0.152$

$a_a$ | $0.535$

$\gamma_{

u}$ | $0.421$

$\gamma_i$ | $0.897$

$\kappa$ | $2.226W/m^2K$

$\epsilon_e$ | $1$

$\epsilon_b$ | $1$

$\epsilon_t$ | $1$

$I_s$ | $342W/m^2$

$T_e$ | $14.8^{\circ}C$

$T_b$ | $1.79^{\circ}C$

$T_t$ | $-30.98^{\circ}C$

ID:(7442, 0)

Bild

>Top

Si se consideran los distintos escenarios B1, A1B y A1 se puede estudiar la probable evolución de la temperatura sobre la superficie del planeta.

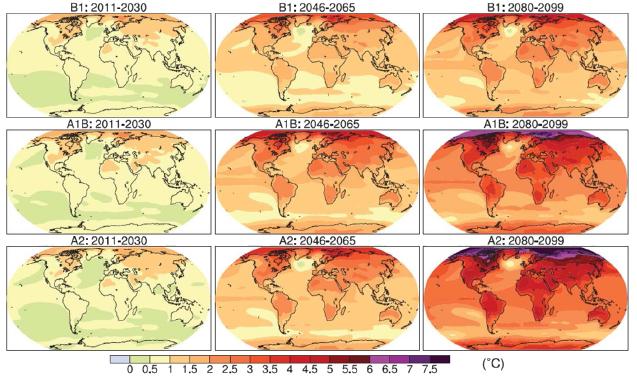
Calentamiento Global bajo distintos escenarios

ID:(7333, 0)

Bild

>Top

La siguiente gráfica muestra el calentamiento según zona geográfica:

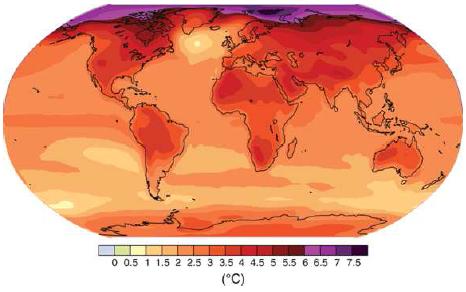
Calentamiento Global (ejemplo)

ID:(7332, 0)