Storyboard

Dans le cas du sol, il est possible de le modéliser en supposant qu'il contient de multiples pores formant de petits capillaires qui le traversent. Sur cette base, il est possible d'appliquer les équations pour le flux laminaire à travers des tubes et de calculer les résistances hydrauliques des réseaux capillaires, qui dépendent de la porosité et donc de la proportion des différents composants.

>Modèle

ID:(370, 0)

Concept

>Top

ID:(15203, 0)

Concept

>Top

Les pores individuels se regroupent pour former des chaînes qui créent des capillaires à travers lesquels l'eau s'écoule.

Pour modéliser ce phénomène, il est nécessaire d'estimer à la fois le rayon de ces capillaires et leur longueur, en tenant compte du fait qu'ils ne sont généralement pas droits.

ID:(937, 0)

Concept

>Top

ID:(2284, 0)

Concept

>Top

A coupe des pores ($S$) inclut a coupe des pores ($S_p$) généré par le nombre de capillaires ($N_p$) :

ID:(2285, 0)

Concept

>Top

Si nous observons une coupe transversale du sol, nous remarquerons que les capillaires passent à travers les espaces entre les grains. En le faisant, leur nombre est similaire à celui des grains eux-mêmes, nous pouvons donc supposer que le nombre de capillaires ($N_p$) est similaire au nombre de grains présents dans la coupe :

ID:(2283, 0)

Concept

>Top

ID:(2291, 0)

Concept

>Top

Le débit total est calculé comme la somme des débits individuels à travers les différents pores :

Si nous supposons que tous les pores sont identiques, nous pouvons obtenir le flux total ($J_{Vt}$) en multipliant le volumique flux ($J_V$) individuellement par le nombre de capillaires ($N_p$).

ID:(2286, 0)

Équation

>Top, >Modèle

Le flux de liquide dans un milieu poreux comme le sol est mesuré à l'aide de la variable a densité de flux ($j_s$), qui représente la vitesse moyenne à laquelle le liquide se déplace à travers celui-ci. Lors de la modélisation du sol et de la manière dont le liquide le traverse, on constate que ce processus est influencé par des facteurs tels que a porosité ($f$) et le rayon d'un grain générique ($r_0$), qui, lorsqu'ils sont plus élevés, facilitent le flux, tandis que a viscosité ($\eta$) entrave le passage à travers les capillaires, réduisant ainsi la vitesse d'écoulement.

Le modèle intègre finalement ce que nous appellerons a conductivité hydraulique ($K_s$), une variable qui dépend des interactions entre le rayon d'un grain générique ($r_0$), a porosité ($f$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a viscosité ($\eta$) et a porosité propre générique ($q_0$) :

$ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$

Conditions

Variables

$J_1$

Calcul de l'équation de porosité

$-$

$J_2$

Facteur de volume propre au slime

$-$

Relation

Développement

Étant donné que a densité de flux ($j_s$) est lié à Le rayon d'un grain générique ($r_0$), a porosité ($f$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a viscosité ($\eta$), a porosité propre générique ($q_0$), a différence de hauteur ($\Delta h$) et le longueur de l'échantillon ($\Delta L$) à travers l'équation :

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$

Nous pouvons définir un facteur que nous appellerons a conductivité hydraulique ($K_s$) comme suit :

$ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$

Ce facteur englobe tous les éléments liés aux propriétés du sol et du liquide qui s'écoule à travers lui.

a conductivité hydraulique ($K_s$) exprime la facilité avec laquelle le liquide est conduit à travers le milieu poreux. En fait, a conductivité hydraulique ($K_s$) augmente avec a porosité ($f$) et le rayon d'un grain générique ($r_0$), et diminue avec a porosité propre générique ($q_0$) et a viscosité ($\eta$).

ID:(4739, 0)

Image

>Top

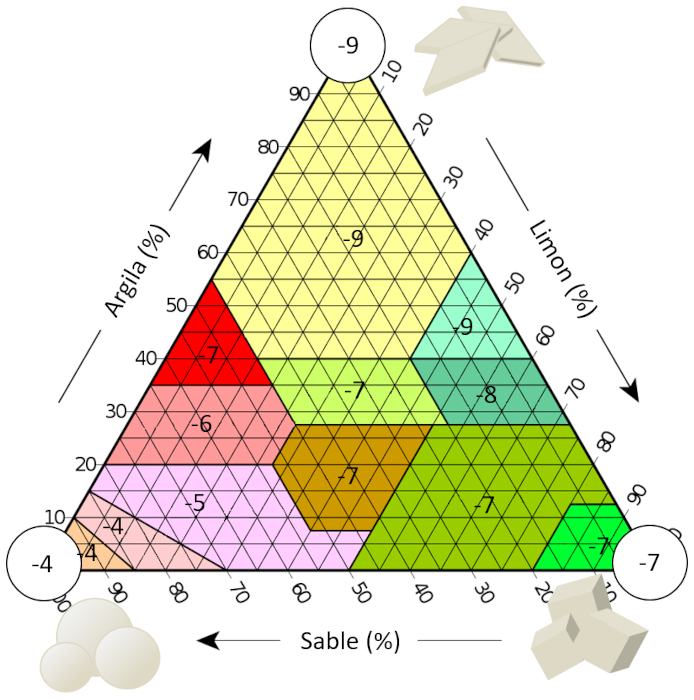
Si nous examinons la littérature, nous pouvons trouver des estimations de la conductivité hydraulique pour différentes textures de sol, qui sont présentées ici en fonction de leur exposant (c'est-à-dire, -7 est indiqué pour une conductivité hydraulique de 1E-7 m/s) :

Les résultats sont résumés dans le tableau suivant :

Ces données ont été obtenues à partir de la littérature suivante, qui est référencée dans la colonne de la conductivité hydraulique :

[1] "Principes et Pratiques de Géotechnique" de Donald P. Coduto et al., Prentice Hall (1999)

[2] "Mécanique des Sols et des Fondations" de Muni Budhu, John Wiley & Sons. (2011)

[3] "Introduction à l'Ingénierie Environnementale" de Mackenzie Davis et David Cornwell, McGraw Hill (2022)

[4] "Principes de Géotechnique" de Braja M. Das, CL-Engineering (2009)

[5] "Mécanique des Sols dans la Pratique de l'Ingénierie" de Karl Terzaghi et Ralph B. Peck, John Wiley & Sons. (1996)

[6] "Mécanique des Sols : Concepts et Applications" de William Powrie, CRC Press (2013)

ID:(4740, 0)

Concept

>Top

Paramètre sélectionné

Calculs

ID:(15222, 0)

Équation

>Top, >Modèle

A porosité ($f$) peut être calculé à partir de a coupe des pores ($S_p$) et a coupe des pores ($S$) en utilisant la formule suivante :

ID:(938, 0)

Équation

>Top, >Modèle

Étant donné que la section transversale d'un pore de rayon du cylindre ($R$) est $\pi R^2$ et que le nombre de capillaires ($N_p$) est lié à cela, nous pouvons calculer a coupe des pores ($S_p$) comme suit :

ID:(4362, 0)

Équation

>Top, >Modèle

Avec a porosité ($f$) et a coupe des pores ($S$), nous obtenons a coupe des pores ($S_p$), que lorsqu'on divise par la section calculée du capillaire de le rayon du cylindre ($R$), donne le nombre de capillaires ($N_p$) comme suit :

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

Conditions

Variables

$N_p$

Nombre de capillaires

$-$

$\pi$

Pi

3.1415927

$rad$

$f$

Porosité

$-$

Relation

Développement

Comme a porosité ($f$), calculé avec a coupe des pores ($S_p$) et a coupe des pores ($S$) en utilisant

$ f = \displaystyle\frac{ S_p }{ S }$

ainsi que l'équation pour le calcul de a coupe des pores ($S_p$) en fonction de le nombre de capillaires ($N_p$) et le rayon du cylindre ($R$) à travers

$ S_p = N_p \pi R ^2$

donne

$f = \displaystyle\frac{N_p\pi R^2}{S}$

peut être résolu pour le nombre de capillaires ($N_p$), ce qui donne

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

ID:(4363, 0)

Équation

>Top, >Modèle

Si nous supposons que le nombre de capillaires est égal au nombre de grains visibles dans une section, nous pouvons démontrer que pour un rayon de grain de le rayon d'un grain générique ($r_0$) et une porosité ($f$), le rayon du cylindre ($R$) sera égal à :

$R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

Conditions

Variables

Relation

Développement

Si nous considérons la zone dans la section qui ne contient pas de pores, en soustrayant a coupe des pores ($S_p$) de a coupe des pores ($S$) et en la divisant par la surface d'un grain générique avec un rayon de rayon d'un grain générique ($r_0$), nous obtenons le nombre de grains visibles dans la section :

$\displaystyle\frac{S-S_p}{\pi r_0^2}=\displaystyle\frac{(1-f)S}{\pi r_0^2}$

où nous utilisons la relation pour a porosité ($f$) :

$ f = \displaystyle\frac{ S_p }{ S }$

Si le nombre de grains est égal à nombre de capillaires ($N_p$) avec l'expression :

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

où le rayon est de le rayon du cylindre ($R$). Avec cela, nous obtenons la relation :

$\displaystyle\frac{(1-f)S}{\pi r_0^2}=\displaystyle\frac{fS}{\pi R^2}$

aboutissant à :

$R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

ID:(109, 0)

Équation

>Top, >Modèle

Si nous égalons le volume d'un capillaire au volume d'une chaîne de grains multiplié par le longueur de l'échantillon ($\Delta L$), nous obtenons une relation entre a longueur capillaire ($l$) et a porosité ($f$) donnée par :

$ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $

Conditions

Variables

Relation

Développement

Le volume du capillaire peut être calculé à partir de le rayon du cylindre ($R$) et a longueur capillaire ($l$), ce qui est égal au volume d'une chaîne de grains de le rayon d'un grain générique ($r_0$) et le longueur du tube ($\Delta L$) multiplié par a porosité propre générique ($q_0$) :

$\pi R^2 l = q_0 \pi r_0^2 \Delta L$

Cela, en conjonction avec a porosité ($f$) dans la relation



donne la relation suivante :

ID:(2215, 0)

Équation

>Top, >Modèle

Le flux total ($J_{Vt}$) est calculé en multipliant ($$) par la valeur de le volumique flux ($J_V$) dans chaque capillaire, comme suit :

$ J_{Vt} = N_p J_V $

Conditions

Variables

$J_{Vt}$

Flux total

$m^3/s$

$N_p$

Nombre de capillaires

$-$

Relation

ID:(4364, 0)

Équation

>Top, >Modèle

Si nous appliquons l'équation de Hagen-Poiseuille à Le volumique flux ($J_V$) pour le cas des capillaires avec le rayon du cylindre ($R$) exprimés en termes de a porosité ($f$) et a longueur capillaire ($l$) en fonction de le longueur de l'échantillon ($\Delta L$), nous pouvons calculer le flux total ($J_{Vt}$) en utilisant

Le résultat peut s'exprimer en termes de a coupe des pores ($S$), a viscosité ($\eta$), a porosité propre générique ($q_0$), le rayon d'un grain générique ($r_0$) et a différence de pression ($\Delta p$) :

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Conditions

Variables

$\Delta p_2$

Différence de pression 2

$Pa$

$L$

Longueur capillaire

$m$

$f$

Porosité

$-$

Relation

Développement

Pour calculer le flux total ($J_{Vt}$) en utilisant le nombre de capillaires ($N_p$) et le volumique flux ($J_V$) pour chaque capillaire à travers

$ J_{Vt} = N_p J_V $

nous obtenons le nombre de capillaires ($N_p$) avec a porosité ($f$), a coupe des pores ($S$) et le rayon du cylindre ($R$) à travers

$ N_p =\displaystyle\frac{ f S }{ \pi R ^2}$

et la loi de Hagen-Poiseuille en utilisant a viscosité ($\eta$), a différence de pression ($\Delta p$) et a longueur capillaire ($l$) est calculée avec

$J_v = - \displaystyle\frac{\pi R^4}{8\eta}\displaystyle\frac{\Delta p}{l}$

En utilisant la relation pour le rayon du cylindre ($R$) en termes de le rayon d'un grain générique ($r_0$)

$R = \sqrt{\displaystyle\frac{ f }{1- f }} r_0 $

et pour a longueur capillaire ($l$), a porosité propre générique ($q_0$) et le longueur de l'échantillon ($\Delta L$)

$ l = q_0 \displaystyle\frac{(1- f )}{ f } \Delta L $

nous obtenons

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Cette équation correspond à l'équation de Kozeny-Carman, qui a été développée par Kozeny et Carman pour modéliser l'écoulement d'un liquide à travers un milieu poreux et a été publiée dans:

• Sur la conduction capillaire de l'eau dans le sol, ("Ueber kapillare Leitung des Wassers im Boden"), J. Kozeny, Sitzungsber Akad. Wiss., Wien, 136(2a) : 271-306 (1927)

• Écoulement des fluides à travers des lits granulaires, ("Fluid flow through granular beds"), P.C. Carman, Transactions, Institution of Chemical Engineers, London, 15 : 150-166 (1937)

• Écoulement des gaz à travers des milieux poreux, ("Flow of gases through porous media"), P.C. Carman, Butterworths, Londres (1956)

ID:(4365, 0)

Équation

>Top, >Modèle

ID:(10594, 0)

Équation

>Top, >Modèle

Dans le cas d'un tube à travers lequel un liquide avec a densité de l'eau ($\rho_w$) s'écoule en raison de a différence de pression ($\Delta p$) généré par une une différence de hauteur ($\Delta h$) sous l'influence de la gravité représentée par a accélération gravitationnelle ($g$) et calculé avec l'équation :

cela peut être utilisé dans l'équation de Hagen-Poiseuille, ainsi qu'avec la définition de a densité de flux ($j_s$) en termes de le flux total ($J_{Vt}$), qui dépend à son tour de le rayon d'un grain générique ($r_0$), a porosité propre générique ($q_0$), a porosité ($f$), a viscosité ($\eta$), et le longueur de l'échantillon ($\Delta L$) :

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$

Conditions

Variables

$\rho_w$

Densité du liquide

$kg/m^3$

$\Delta h$

Différence de hauteur ou de profondeur

$m$

$L$

Longueur capillaire

$m$

$f$

Porosité

$-$

Relation

Développement

Dans le cas des capillaires à travers lesquels un liquide avec a densité du liquide ($\rho_w$) s'écoule en raison de a différence de pression ($\Delta p$) généré par une différence de hauteur ($\Delta h$) sous l'influence de la gravité représentée par a accélération gravitationnelle ($g$) et calculé avec l'équation :

$ \Delta p = \rho_w g \Delta h $

cela peut être appliqué dans l'équation de Hagen-Poiseuille, en termes de le flux total ($J_{Vt}$), qui dépend à son tour de le rayon d'un grain générique ($r_0$), a porosité propre générique ($q_0$), a porosité ($f$), a viscosité ($\eta$), a coupe ou surface ($S$) et le longueur de l'échantillon ($\Delta L$) comme décrit dans l'équation :

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $

Avec la définition de a densité de flux ($j_s$) :

$j_s = \displaystyle\frac{J_{Vt}}{S}$

Nous avons :

$j_s=\displaystyle\frac{J_{Vt}}{S}=\displaystyle\frac{ r_0 ^2 }{8 q_g }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ L }$

ce qui donne :

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$

ID:(4366, 0)

Équation

>Top, >Modèle

Pour établir une relation entre la conductivité hydraulique et les facteurs de masse, nous introduisons le facteur d'échelle capillaire ($\gamma$) avec le rayon d'un grain générique ($r_0$), le rayon du grain de sable ($r_a$), a porosité propre générique ($q_0$) et a porosité du sable ($q_a$) comme

$ \gamma = \displaystyle\frac{ r_0 ^2}{ r_a ^2}\displaystyle\frac{ q_a }{ q_0 }$

Conditions

Variables

Relation

.

ID:(15101, 0)

Équation

>Top, >Modèle

À partir de la définition de a conductivité hydraulique ($K_s$) et le facteur d'échelle capillaire ($\gamma$), nous pouvons exprimer a conductivité hydraulique ($K_s$) en fonction de le rayon du grain de sable ($r_a$), a porosité du sable ($q_a$), a porosité ($f$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$) et a viscosité ($\eta$) comme suit :

$ K_s = \displaystyle\frac{ r_a ^2}{8 q_a }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta } \gamma $

Conditions

Variables

Relation

.

ID:(977, 0)

Équation

>Top, >Modèle

Le calcul de le facteur d'échelle capillaire ($\gamma$) est dérivé de a porosité ($f$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$) et a viscosité ($\eta$), en excluant le rayon du grain de sable ($r_a$) et a porosité du sable ($q_a$), à travers l'équation suivante :

$\gamma=\displaystyle\frac{8K_sq_a}{r_a^2}\displaystyle\frac{(1-f)^2}{f^3}\displaystyle\frac{\eta}{\rho_wg}$

Si nous voulons relier le facteur d'échelle capillaire ($\gamma$) à A fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$), nous observons que tandis que le premier varie de 6 ordres de grandeur, les derniers ne varient que de 2 ordres de grandeur. Il est donc logique d'établir une relation avec le logarithme naturel de $\gamma$. Ainsi, nous effectuons une régression en utilisant l'équation suivante :

$\ln \gamma = s_a g_a + s_i g_i + s_c g_c $

Conditions

Variables

Relation

avec le facteur de section capillaire dans le sable ($s_a$), le facteur de section capillaire dans le limon ($s_i$) et le facteur de section capillaire d'argile ($s_c$).

Les données moyennes pour chaque intervalle sont les suivantes :

La régression donne une relation linéaire avec une valeur de R carré de 0,9975 et les coefficients suivants, ainsi que les valeurs pour évaluer la qualité des coefficients :

Étant donné les valeurs du test de p, nous pouvons supposer que tous les coefficients sont hautement pertinents.

ID:(15100, 0)