Hydrostatic Pressure
Storyboard 
In the case of saturated soil, porosity is filled with water. The presence of water implies additional mass and the existence of pressure as a function of depth. Both factors will affect the behavior of the soil.
ID:(368, 0)
Description of the water column
Image 
To study the behavior of liquids, it is useful to introduce the concept of a column of liquid. This column is an abstraction of a cylindrical container (such as a graduated cylinder) containing liquid, and allows us to study the force to which an object inside it is exposed.
Once this concept is introduced, we can think of its existence independently of the container that contains it. For example, a diver swimming in open sea is exposed to the weight generated by an 'imaginary' column of liquid that exists above them, from the surface of the liquid to their skin and the surface of the sea.
the mass of liquid column ($M$) can be calculated from the liquid density ($\rho_w$) and the column volume ($V$).
To calculate the liquid density ($\rho_w$), the following equation is used:
| $ \rho_w = \displaystyle\frac{ M }{ V }$ |
And for the column volume ($V$), the equation is:
| $ V = S h $ |
This way, the value of the mass of liquid column ($M$) is obtained by:
| $ M = \rho_w S h $ |
This is valid as long as the column Section ($S$) remains constant throughout the column height ($h$).
The section may change in its shape, but not in its surface.
ID:(2207, 0)
Force of water on the bottom of the column
Note 
Once the volume and thus the mass of the column is known, the force it exerts on its bottom can be calculated. It is important to note that this applies to liquids that are considered incompressible, which means that the lower layers of the liquid are assumed not to be compressed by the weight of the layers above them.
This principle can be applied to calculate the force exerted by any liquid, such as water or oil, and is particularly useful in hydraulic engineering and fluid mechanics.
Since the mass of liquid column ($M$) depends on the liquid density ($\rho_w$), the column Section ($S$), and the column height ($h$) according to the equation:
| $ M = \rho_w S h $ |
and the column force ($F$) is represented with the gravitational Acceleration ($g$) by:
| $ F_g = m_g g $ |
the expression can be written as follows:
| $ F = S h \rho_w g $ |
.
ID:(2208, 0)
Introduction of the concept of pressure
Quote 
In mechanics, we describe how bodies with defined mass move. In the case of a liquid, its movement is not uniform, and each section of the liquid moves differently. However, these \\"sections\\" do not have a defined mass, as they are not defined or separate objects.
To address this issue, we can segment the liquid into a series of small, separated volumes and, if possible, estimate their mass using density. In this way, we can introduce the idea that forces define the movement of the liquid.
However, ultimately volumes are arbitrary, and what ultimately generates the movement is the force acting on the volume's face. Therefore, it makes more sense to introduce the concept of ERROR:10113,0 per such ERROR:6002,0, which is called the water column pressure ($p$).
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
ID:(46, 0)
Water pressure on the bottom of the column
Exercise 
The the column force ($F$) acting on the bottom depends on the column Section ($S$) in the sense that if the latter varies, the force will vary in the same proportion. In this sense, the column force ($F$) and the column Section ($S$) are not interdependent; they vary proportionally. It makes sense to define this proportion as the pressure ($p$):
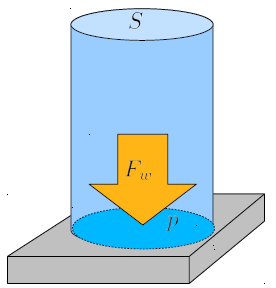
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
| $ F = S h \rho_w g $ |
and the the water column pressure ($p$) is then defined as
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
we have that the the water column pressure ($p$) generated by a column of liquid is
| $ p = \rho_w g h $ |
This is the law of hydrostatic pressure, also known as Pascal's Law, primarily attributed to Blaise Pascal [1].
![]() [1] "Traité de l'équilibre des liqueurs" (Treatise on the Equilibrium of Liquids), Blaise Pascal, 1663.
[1] "Traité de l'équilibre des liqueurs" (Treatise on the Equilibrium of Liquids), Blaise Pascal, 1663.
ID:(2085, 0)
Sum of column pressure and atmosphere
Equation 
If it is considered that the column is influenced by the atmospheric pressure ($p_0$), then the contribution of the atmospheric pressure ($p_0$) must be added to the water column pressure ($p$) of the column, as shown here:
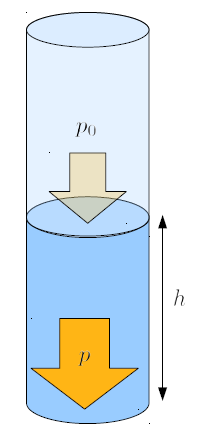
When calculating the water column pressure ($p$) at a certain depth, it's important to consider that the liquid's surface is exposed to the atmospheric pressure ($p_0$), which can affect the pressure value at that point. Therefore, it's necessary to generalize the equation for the water column pressure ($p$) to include not only the liquid column the liquid density ($\rho_w$), the column height ($h$), and the gravitational Acceleration ($g$) but also the atmospheric pressure ($p_0$):
| $ p_t = p_0 + \rho_w g h $ |
It is not always necessary to consider atmospheric pressure in the modeling:
In many cases, atmospheric pressure is present throughout the system, so pressure differences do not depend on it.
ID:(2210, 0)
Connecting two liquid columns
Script 
If two columns of water with different heights at their bases are connected, a situation arises where there is a pressure difference along the connecting tube.
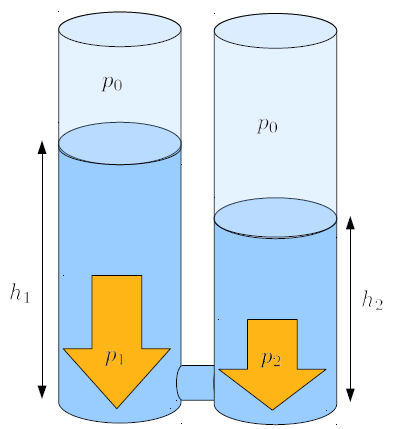
This setup allows us to study how the pressure difference generates a liquid flow along the tube. We can consider an element of liquid with a certain length and a section equal to that of the tube, and estimate the corresponding mass using the density. With the section, we can also convert the pressure difference into a force difference and, ultimately, study how volumes in liquids are accelerated due to pressure differences.
ID:(933, 0)
Hydrostatic Pressure
Storyboard 
In the case of saturated soil, porosity is filled with water. The presence of water implies additional mass and the existence of pressure as a function of depth. Both factors will affect the behavior of the soil.
Variables
Calculations
Calculations
Equations
Since the mass of liquid column ($M$) depends on the liquid density ($\rho_w$), the column Section ($S$), and the column height ($h$) according to the equation:
and the column force ($F$) is represented with the gravitational Acceleration ($g$) by:
the expression can be written as follows:
Since the mass of liquid column ($M$) depends on the liquid density ($\rho_w$), the column Section ($S$), and the column height ($h$) according to the equation:
and the column force ($F$) is represented with the gravitational Acceleration ($g$) by:
the expression can be written as follows:
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
and the the water column pressure ($p$) is then defined as
we have that the the water column pressure ($p$) generated by a column of liquid is
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
and the the water column pressure ($p$) is then defined as
we have that the the water column pressure ($p$) generated by a column of liquid is
The mass of liquid column ($M$) can be calculated from the liquid density ($\rho_w$) and the column volume ($V$).
To calculate the liquid density ($\rho_w$), the following equation is used:
And for the column volume ($V$), the equation is:
This way, the value of the mass of liquid column ($M$) is obtained by:
The mass of liquid column ($M$) can be calculated from the liquid density ($\rho_w$) and the column volume ($V$).
To calculate the liquid density ($\rho_w$), the following equation is used:
And for the column volume ($V$), the equation is:
This way, the value of the mass of liquid column ($M$) is obtained by:
If there is the pressure difference ($\Delta p$) between two points, as determined by the equation:
we can utilize the water column pressure ($p$), which is defined as:
This results in:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
As the height difference ($\Delta h$) is:
the pressure difference ($\Delta p$) can be expressed as:
Examples
To study the behavior of liquids, it is useful to introduce the concept of a column of liquid. This column is an abstraction of a cylindrical container (such as a graduated cylinder) containing liquid, and allows us to study the force to which an object inside it is exposed.
Once this concept is introduced, we can think of its existence independently of the container that contains it. For example, a diver swimming in open sea is exposed to the weight generated by an 'imaginary' column of liquid that exists above them, from the surface of the liquid to their skin and the surface of the sea.
the mass of liquid column ($M$) can be calculated from the liquid density ($\rho_w$) and the column volume ($V$).
To calculate the liquid density ($\rho_w$), the following equation is used:
And for the column volume ($V$), the equation is:
This way, the value of the mass of liquid column ($M$) is obtained by:
This is valid as long as the column Section ($S$) remains constant throughout the column height ($h$).
The section may change in its shape, but not in its surface.
Once the volume and thus the mass of the column is known, the force it exerts on its bottom can be calculated. It is important to note that this applies to liquids that are considered incompressible, which means that the lower layers of the liquid are assumed not to be compressed by the weight of the layers above them.
This principle can be applied to calculate the force exerted by any liquid, such as water or oil, and is particularly useful in hydraulic engineering and fluid mechanics.
Since the mass of liquid column ($M$) depends on the liquid density ($\rho_w$), the column Section ($S$), and the column height ($h$) according to the equation:
and the column force ($F$) is represented with the gravitational Acceleration ($g$) by:
the expression can be written as follows:
In mechanics, we describe how bodies with defined mass move. In the case of a liquid, its movement is not uniform, and each section of the liquid moves differently. However, these \\"sections\\" do not have a defined mass, as they are not defined or separate objects.
To address this issue, we can segment the liquid into a series of small, separated volumes and, if possible, estimate their mass using density. In this way, we can introduce the idea that forces define the movement of the liquid.
However, ultimately volumes are arbitrary, and what ultimately generates the movement is the force acting on the volume's face. Therefore, it makes more sense to introduce the concept of ERROR:10113,0 per such ERROR:6002,0, which is called the water column pressure ($p$).
The the column force ($F$) acting on the bottom depends on the column Section ($S$) in the sense that if the latter varies, the force will vary in the same proportion. In this sense, the column force ($F$) and the column Section ($S$) are not interdependent; they vary proportionally. It makes sense to define this proportion as the pressure ($p$):
As the the column force ($F$) generated by a column of liquid of the column height ($h$), the column Section ($S$), the liquid density ($\rho_w$), and the gravitational Acceleration ($g$) is
and the the water column pressure ($p$) is then defined as
we have that the the water column pressure ($p$) generated by a column of liquid is
This is the law of hydrostatic pressure, also known as Pascal's Law, primarily attributed to Blaise Pascal [1].
![]() [1] "Trait de l' quilibre des liqueurs" (Treatise on the Equilibrium of Liquids), Blaise Pascal, 1663.
[1] "Trait de l' quilibre des liqueurs" (Treatise on the Equilibrium of Liquids), Blaise Pascal, 1663.
If it is considered that the column is influenced by the atmospheric pressure ($p_0$), then the contribution of the atmospheric pressure ($p_0$) must be added to the water column pressure ($p$) of the column, as shown here:
When calculating the water column pressure ($p$) at a certain depth, it's important to consider that the liquid's surface is exposed to the atmospheric pressure ($p_0$), which can affect the pressure value at that point. Therefore, it's necessary to generalize the equation for the water column pressure ($p$) to include not only the liquid column the liquid density ($\rho_w$), the column height ($h$), and the gravitational Acceleration ($g$) but also the atmospheric pressure ($p_0$):
It is not always necessary to consider atmospheric pressure in the modeling:
In many cases, atmospheric pressure is present throughout the system, so pressure differences do not depend on it.
If two columns of water with different heights at their bases are connected, a situation arises where there is a pressure difference along the connecting tube.
This setup allows us to study how the pressure difference generates a liquid flow along the tube. We can consider an element of liquid with a certain length and a section equal to that of the tube, and estimate the corresponding mass using the density. With the section, we can also convert the pressure difference into a force difference and, ultimately, study how volumes in liquids are accelerated due to pressure differences.
The column volume ($V$) is determined by the column Section ($S$) and the column height ($h$), and it is calculated as follows:
The column volume ($V$) is determined by the column Section ($S$) and the column height ($h$), and it is calculated as follows:
The the liquid density ($\rho_w$) is calculated from the mass of liquid column ($M$) and the column volume ($V$) using the equation:
The the liquid density ($\rho_w$) is calculated from the mass of liquid column ($M$) and the column volume ($V$) using the equation:
Using the liquid density ($\rho_w$), the column Section ($S$), and the column height ($h$), you can calculate the mass of liquid column ($M$) with the formula:
Using the liquid density ($\rho_w$), the column Section ($S$), and the column height ($h$), you can calculate the mass of liquid column ($M$) with the formula:
The column force ($F$) is calculated from the column Section ($S$), the liquid density ($\rho_w$), the column height ($h$) and the gravitational Acceleration ($g$) using:
The column force ($F$) is calculated from the column Section ($S$), the liquid density ($\rho_w$), the column height ($h$) and the gravitational Acceleration ($g$) using:
The water column pressure ($p$) is calculated from the column force ($F$) and the column Section ($S$) as follows:
The water column pressure ($p$) is calculated from the column force ($F$) and the column Section ($S$) as follows:
If we consider the expression of the column force ($F$) and divide it by the column Section ($S$), we obtain the water column pressure ($p$). In this process, we simplify the column Section ($S$), so it no longer depends on it. The resulting expression is:
If we consider the expression of the column force ($F$) and divide it by the column Section ($S$), we obtain the water column pressure ($p$). In this process, we simplify the column Section ($S$), so it no longer depends on it. The resulting expression is:
The water column pressure ($p$) is with the liquid density ($\rho_w$), the column height ($h$), the gravitational Acceleration ($g$) and the atmospheric pressure ($p_0$) equal to:
The water column pressure ($p$) is with the liquid density ($\rho_w$), the column height ($h$), the gravitational Acceleration ($g$) and the atmospheric pressure ($p_0$) equal to:
When two liquid columns are connected with the height of liquid column 1 ($h_1$) and the height of liquid column 2 ($h_2$), a the height difference ($\Delta h$) is formed, which is calculated as follows:
the height difference ($\Delta h$) will generate the pressure difference that will cause the liquid to flow from the higher column to the lower one.
When two liquid columns are connected with the pressure in column 1 ($p_1$) and the pressure in column 2 ($p_2$), a the pressure difference ($\Delta p$) is formed, which is calculated according to the following formula:
the pressure difference ($\Delta p$) represents the pressure difference that will cause the liquid to flow from the taller column to the shorter one.
The height difference, denoted by the height difference ($\Delta h$), implies that the pressure in both columns is distinct. In particular, the pressure difference ($\Delta p$) is a function of the liquid density ($\rho_w$), the gravitational Acceleration ($g$), and the height difference ($\Delta h$), as follows:
ID:(368, 0)
