Wahrnehmung von Entfernung
Definition 
Wir haben zwei Augen, so dass wir Distanzen schätzen können und somit eine dreidimensionale Wahrnehmung haben.
ID:(433, 0)
Modellierung des Blicks auf ein Objekt
Notiz 
Um zu modellieren, müssen wir die Situation, die mit den Bildern in beiden Netzhäuten auftritt, grafisch darstellen. Um dies zu tun, untersuchten wir das Verhalten von zwei Strahlen in der Ebene zwischen dem Objekt und den beiden Netzhäuten.
Angenommen, die Positionen des Bildes im linken und im rechten Auge sind
ID:(436, 0)
Geometrie für Entfernungsmessung mit dem Auge
Zitat 
Die Position eines Objekts wird von jedem Auge unterschiedlich wahrgenommen. Das Bild wird in verschiedenen Punkten in Bezug auf das Zentrum der Netzhaut gebildet:
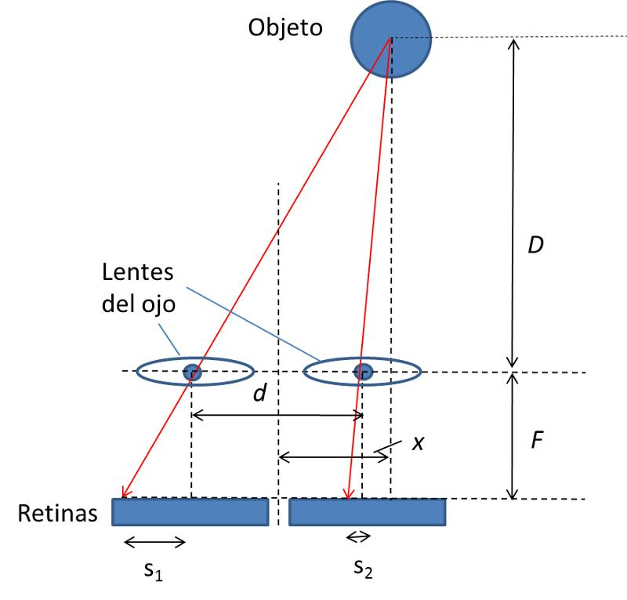
Aus der Positionsdifferenz können wir die Position des Objekts in Bezug auf uns bestimmen.
ID:(1665, 0)
Gleichung Dreieck Linkes Auge
Übung 
Durch Ähnlichkeit der Dreiecke kann der Anteil der Dreiecke des linken Auges ausgeglichen werden. Im Fall des Hauptdreiecks haben die Seiten die Längen
ID:(434, 0)
Gleichung Dreieck Rechtes Auge
Gleichung 
Durch Ähnlichkeit der Dreiecke kann der Anteil der Dreiecke des rechten Auges gleichgesetzt werden. Im Falle des großen Dreiecks haben die Seiten die Längen
ID:(435, 0)
Fehler beim Entfernungen Schätzung
Script 
Der Fehler der Schätzung kann berechnet werden, indem die Unsicherheits-Ausbreitungsgleichungen auf dem Ausdruck für die Berechnung der Entfernung verwendet werden. Um die Berechnung zu vereinfachen, können wir den Ausdruck für den Fall verwenden, dass das Objekt vor uns liegt.
ID:(193, 0)
Medir Distancias
Storyboard 
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
Wir haben zwei Augen, so dass wir Distanzen sch tzen k nnen und somit eine dreidimensionale Wahrnehmung haben.
Effekt des Sehens mit zwei Augen
Um zu modellieren, m ssen wir die Situation, die mit den Bildern in beiden Netzh uten auftritt, grafisch darstellen. Um dies zu tun, untersuchten wir das Verhalten von zwei Strahlen in der Ebene zwischen dem Objekt und den beiden Netzh uten.
Angenommen, die Positionen des Bildes im linken und im rechten Auge sind
Die Position eines Objekts wird von jedem Auge unterschiedlich wahrgenommen. Das Bild wird in verschiedenen Punkten in Bezug auf das Zentrum der Netzhaut gebildet:
Aus der Positionsdifferenz k nnen wir die Position des Objekts in Bezug auf uns bestimmen.
Durch hnlichkeit der Dreiecke kann der Anteil der Dreiecke des linken Auges ausgeglichen werden. Im Fall des Hauptdreiecks haben die Seiten die L ngen
Durch hnlichkeit der Dreiecke kann der Anteil der Dreiecke des rechten Auges gleichgesetzt werden. Im Falle des gro en Dreiecks haben die Seiten die L ngen
Aus den Gleichungen des Dreiecks des linken und rechten Auges k nnen wir den Abstand des Objekts in der Ebene der Augen
Hinweis: Es kann gezeigt werden, dass die Summe
Die Entfernung des Objekts kann aus den Gleichungen des linken und rechten Dreiecks bestimmt werden. Auf diese Weise erhalten wir, dass der Abstand Hinweis: Es kann gezeigt werden, dass die Summe
Um zu der tats chlichen Entfernung
Um zu der tats chlichen Entfernung
Der Fehler der Sch tzung kann berechnet werden, indem die Unsicherheits-Ausbreitungsgleichungen auf dem Ausdruck f r die Berechnung der Entfernung verwendet werden. Um die Berechnung zu vereinfachen, k nnen wir den Ausdruck f r den Fall verwenden, dass das Objekt vor uns liegt.
Um die L sung des Modells zu vereinfachen, ist es ratsam, die Arbeit mit dem Winkel
Der projizierte Abstand des Objekts ist
Diese nderung entspricht der Bewegung von Polarkoordinaten (
Um zu der tats chlichen Entfernung
$\Delta r=\displaystyle\frac{2r^2}{df}$
$r= \sqrt{D^2+F^2}$
$F=r\sin\theta$
$r=\displaystyle\frac{df}{2s}$
$\displaystyle\frac{\Delta r^2}{r^2}=\displaystyle\frac{\Delta s^2}{s^2}+\displaystyle\frac{\Delta d^2}{d^2}+\displaystyle\frac{\Delta f^2}{f^2}$
ID:(291, 0)