Percepción de distancia
Definición 
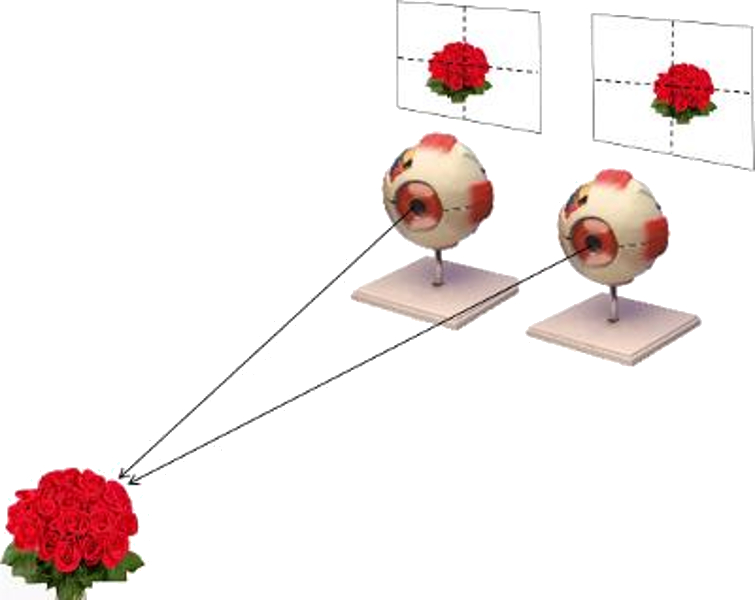
Nosotros tenemos dos ojos de modo que somos capaces de estimar distancias y tener asi una percepción tridimensional.
ID:(433, 0)
Modelamiento de la vista de un objeto
Nota 
Para modelar debemos diagramar la situación que se da con las imágenes en ambas retinas. Para ello estudiamos el comportamiento de dos haces en el plano formado entre objeto y las dos retinas.
Supongamos que las posiciones de la imagen en el ojo izquierdo y derecho son
ID:(436, 0)
Geometría para la medición de distancia con el ojo
Cita 
La posición de un objeto se percibe distinta por cada ojo. La imagen se forma en distintos puntos respecto del centro de la retina:
Forma como la imagen observada se percibe por cada ojo
De la diferencia en la posición somos capaces de determinar la posición que tiene el objeto respecto de nosotros.
ID:(1665, 0)
Ecuación triangulo ojo izquierdo
Ejercicio 
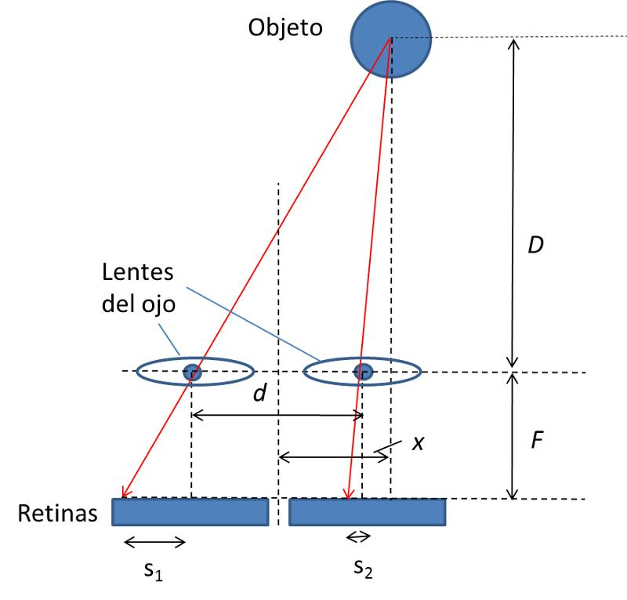
Por similitud de los triángulos se puede igualar la proporción de los triángulos del ojo izquierdo. En el caso del triangulo mayor los lados tienen largos
ID:(434, 0)
Ecuación triangulo ojo derecho
Ecuación 
Por similitud de los triángulos se puede igualar la proporción de los triángulos del ojo derecho. En el caso del triangulo mayor los lados tienen largos
ID:(435, 0)
Error del calculo de la distancia
Script 
El error de la estimación se puede calcular empelando las ecuaciones de propagación de incerteza sobre la expresión para el calculo de la distancia. Para simplificar el calculo se puede emplear la expresión para el caso que el objeto este frente a nosotros.
ID:(193, 0)
Limitación en la determinación de la distancia
Variable 
Aun cuando existe una relación entre distancia de un objeto y el corrimiento de las imagenes en la retina no significa que nuestros ojos puedan determinar cualquier distancia. La limitante esta dada por el error que incluye la estimación. Si el error es demasiado grande la estimación puede carecer de todo sentido.
ID:(453, 0)
Rango en que podemos estimar distancias
Audio 
La incerteza de la posición de la imagen en la retina se puede asumida igual a la distancia entre conos.
Si se asume una distancia entre ojos
ID:(454, 0)
Detalle de bastones del ojo
Video 
Capacidad de resolver en la retina

Estructura del ojo
ID:(1824, 0)
Medir Distancias
Storyboard 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Nosotros tenemos dos ojos de modo que somos capaces de estimar distancias y tener asi una percepci n tridimensional.
Efecto de ver con dos ojos
Para modelar debemos diagramar la situaci n que se da con las im genes en ambas retinas. Para ello estudiamos el comportamiento de dos haces en el plano formado entre objeto y las dos retinas.
Supongamos que las posiciones de la imagen en el ojo izquierdo y derecho son
La posici n de un objeto se percibe distinta por cada ojo. La imagen se forma en distintos puntos respecto del centro de la retina:
De la diferencia en la posici n somos capaces de determinar la posici n que tiene el objeto respecto de nosotros.
Por similitud de los tri ngulos se puede igualar la proporci n de los tri ngulos del ojo izquierdo. En el caso del triangulo mayor los lados tienen largos
Por similitud de los tri ngulos se puede igualar la proporci n de los tri ngulos del ojo derecho. En el caso del triangulo mayor los lados tienen largos
De las ecuaciones del triangulo del ojo izquierdo y derecho se puede determinar la distancia del objeto en el plano de los ojos
Nota: se puede mostrar que la suma
De las ecuaciones del triangulo del ojo izquierdo y derecho se puede determinar la distancia del objeto. De esta forma se obtiene que la distancia
Nota: se puede mostrar que la suma
Para volver a lo que es la distancia real
Para volver a lo que es la distancia real
El error de la estimaci n se puede calcular empelando las ecuaciones de propagaci n de incerteza sobre la expresi n para el calculo de la distancia. Para simplificar el calculo se puede emplear la expresi n para el caso que el objeto este frente a nosotros.
Para simplificar la soluci n del modelo es recomendable evitar trabajar con el angulo
La distancia proyectada del objeto es
Dicho cambio corresponde pasar de coordenadas polares (
Para volver a lo que es la distancia real
Tanto la distancia entre ojos
Esto significa que el error aumenta con el cuadrado de la distancia.
Para volver a lo que es la distancia real
Para simplificar la soluci n del modelo es recomendable evitar trabajar con el angulo
La distancia perpendicular del Objeto es
Dicho cambio corresponde pasar de coordenadas polares (
Si el objeto se encuentra frente a nosotros, el desplazamiento observado en el ojo sera igual pero de signo opuesto al del desplazamiento en el ojo derecho (
Como el ojo es de un tama o finito, la distancia m nima que podemos medir esta determinado por el desplazamiento m ximo
Aun cuando existe una relaci n entre distancia de un objeto y el corrimiento de las imagenes en la retina no significa que nuestros ojos puedan determinar cualquier distancia. La limitante esta dada por el error que incluye la estimaci n. Si el error es demasiado grande la estimaci n puede carecer de todo sentido.
La incerteza de la posici n de la imagen en la retina se puede asumida igual a la distancia entre conos.
Si se asume una distancia entre ojos
Capacidad de resolver en la retina
Empleando la expresi n para el calculo de la distancia del caso simple y la ecuaci n de propagaci n de errores se obtiene la expresi n:
ID:(291, 0)