Modelo de superfície
Storyboard 
A transferência de partículas ou moléculas, como o CO2, entre a atmosfera e o oceano envolve um mecanismo mais complexo. Este processo está associado à formação de um filme líquido saturado com partículas ou moléculas, que regula o movimento de novas partículas para dentro ou para fora do interior do oceano.
ID:(1633, 0)
Camada superficial
Descrição 
Para estudar a transferência de CO2 na superfície do oceano, é necessário observar em detalhes o que acontece com as concentrações tanto no ar como na água.
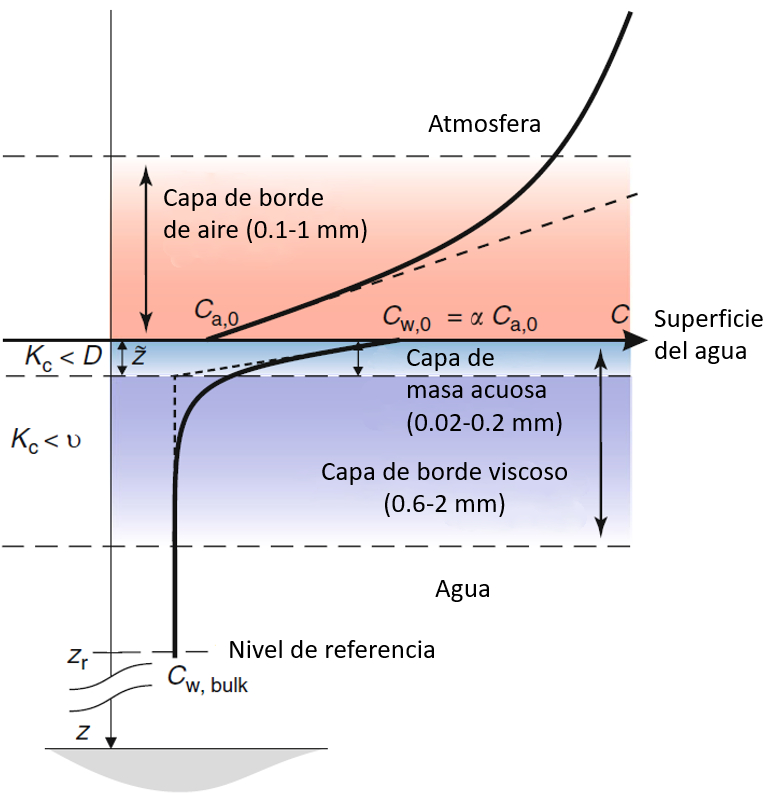
No ar, o CO2 entra na água criando uma região de baixa concentração, onde diminui de $C_a$ para $C_{a,0}$. Essa camada tem uma espessura entre 0,1 e 1 mm.
O CO2 que entra na água se acumula inicialmente na superfície, criando uma concentração $C_{w,0}$, que posteriormente difunde para o interior, alcançando uma concentração menor $C_w$.
A redução da concentração permite definir duas zonas: uma muito fina, de apenas 0,02 a 0,2 mm, onde a concentração diminui rapidamente, e uma segunda zona de 0,6 a 2 mm, onde a concentração diminui de forma mais suave até atingir a concentração no interior da água.
ID:(12244, 0)
Troca de CO2, velocidade da água
Conceito 
La taxa de transferência de gás na água ($k_w$) pode ser modelada usando dados medidos. Em primeiro lugar, depende da velocidade com que o sistema remove carbono da interface ar-água, tornando a velocidade de transporte proporcional à velocidade relativa entre os dois meios.
Em segundo lugar, há um efeito da mobilidade dos íons, que pode ser descrito por o número Schmidt ($Sc$), representando a relação entre a difusão de momento e as partículas. No entanto, essa dependência não é linear e é influenciada por um fator ERROR:9926 que varia entre -1/2 e -2/3 dependendo da rugosidade da superfície.
Finalmente, la taxa de transferência de gás na água ($k_w$) também depende de ERROR:9409, que por sua vez é determinada pelo nível de rugosidade da superfície.
Em resumo, o gás la taxa de transferência de gás na água ($k_w$) é descrito em função de ERROR:9437, ERROR:9408, o número Schmidt ($Sc$), ERROR:9409 e ERROR:9926 da seguinte maneira:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(15652, 0)
Solubilidade em função do número de Schmidt
Conceito 
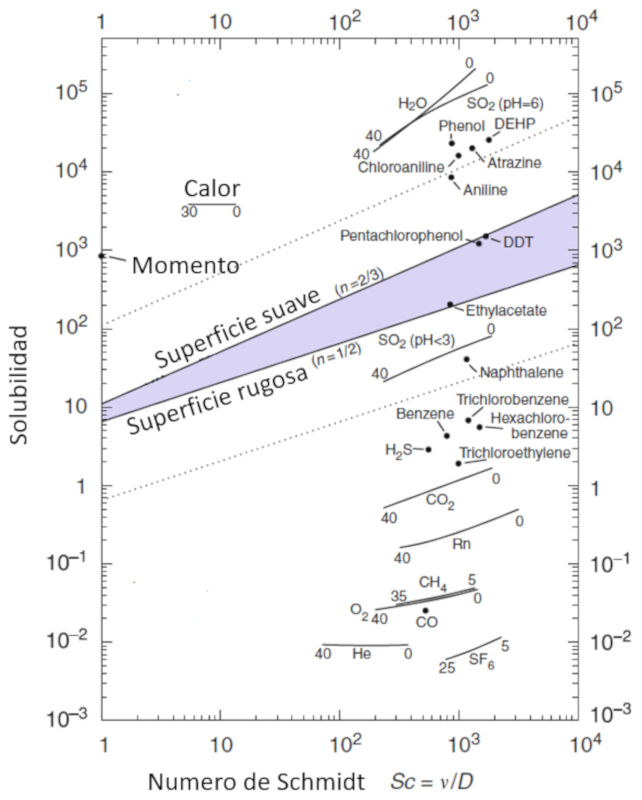
A mobilidade das moléculas, representada por la solubilidade de gás ($\alpha$), é uma função da concentração de partículas, descrita por o número Schmidt ($Sc$), que por sua vez é calculada a partir de ERROR:9412, ERROR:9413 e ERROR:9414 utilizando a seguinte equação:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
Essa relação é ilustrada no seguinte diagrama:
ID:(12245, 0)
Velocidade de transferência
Conceito 
La taxa de transferência de gás no ar ($k_a$) pode ser estimado a partir da lei de Fick, comparando ERROR:9414 com ERROR:9430 da seguinte maneira:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
ID:(15653, 0)
Velocidade de transferência e resistências
Conceito 
Para a interação entre a atmosfera e o oceano, la resistência à transferência de ar para água de um gás ($R_{ta}$) inclui inicialmente la resistência à transferência na água ($R_w$), seguido pelo processo de evaporação $1/\alpha$ com la solubilidade de gás ($\alpha$), e, uma vez que o gás tenha passado para o ar, la resistência de transferência no ar ($R_a$) age sobre ele:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
Já para a interação entre a atmosfera e o oceano, la resistência à transferência de água para ar de um gás ($R_{tw}$) inclui inicialmente la resistência de transferência no ar ($R_a$), seguido de la solubilidade de gás ($\alpha$), e, uma vez que o gás tenha penetrado na água, age la resistência à transferência na água ($R_w$):
| $ R_{tw} = R_w + \alpha R_a $ |
Com essas equações, podemos formular as equações para as velocidades de transferência.
Assim, utilizando la taxa total de transferência de gás no ar ($k_{ta}$), la taxa de transferência de gás na água ($k_w$), la taxa de transferência de gás no ar ($k_a$) e la solubilidade de gás ($\alpha$), estabelecemos a seguinte relação:
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
Por outro lado, com la taxa total de transferência de gás na água ($k_{tw}$), la taxa de transferência de gás na água ($k_w$), la taxa de transferência de gás no ar ($k_a$) e la solubilidade de gás ($\alpha$), estabelecemos que:
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
ID:(15654, 0)
Modelo de superfície
Modelo 
A transferência de partículas ou moléculas, como o CO2, entre a atmosfera e o oceano envolve um mecanismo mais complexo. Este processo está associado à formação de um filme líquido saturado com partículas ou moléculas, que regula o movimento de novas partículas para dentro ou para fora do interior do oceano.
Variáveis
Cálculos
Cálculos
Equações
A rela o envolvendo la resistência à transferência de ar para água de um gás ($R_{ta}$), determinada pela combina o de la resistência à transferência na água ($R_w$), la resistência de transferência no ar ($R_a$) e la solubilidade de gás ($\alpha$), formulada na equa o:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
Isso inclui a rela o de la resistência de transferência no ar ($R_a$) com la taxa de transferência de gás no ar ($k_a$) expressa em:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
Al m disso, a intera o de la resistência à transferência na água ($R_w$) com la taxa de transferência de gás na água ($k_w$) explicada em:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
E a conex o entre la resistência à transferência de ar para água de um gás ($R_{ta}$) e la taxa total de transferência de gás no ar ($k_{ta}$) especificada em:
| $ R_{ta} = \displaystyle\frac{1}{ k_{ta} } $ |
Esses elementos juntos fornecem a base para definir a rela o para la taxa total de transferência de gás no ar ($k_{ta}$):
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
(ID 12242)
A rela o entre la resistência à transferência de água para ar de um gás ($R_{tw}$), estabelecida atrav s das somas de la resistência à transferência na água ($R_w$), la resistência de transferência no ar ($R_a$) e la solubilidade de gás ($\alpha$), expressa na equa o:
| $ R_{tw} = R_w + \alpha R_a $ |
Incluindo a rela o de la resistência de transferência no ar ($R_a$) com la taxa de transferência de gás no ar ($k_a$) em:
| $ R_a = \displaystyle\frac{1}{ k_a } $ |
A intera o de la resistência à transferência na água ($R_w$) com la taxa de transferência de gás na água ($k_w$) descrita em:
| $ R_w = \displaystyle\frac{1}{ k_w } $ |
E a conex o entre la resistência à transferência de água para ar de um gás ($R_{tw}$) e la taxa total de transferência de gás na água ($k_{tw}$) detalhada em:
| $ R_{tw} = \displaystyle\frac{1}{ k_{tw} } $ |
Isso fornece a base para estabelecer a rela o para la taxa total de transferência de gás na água ($k_{tw}$):
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
(ID 12243)
Exemplos
(ID 15640)
Para estudar a transfer ncia de CO2 na superf cie do oceano, necess rio observar em detalhes o que acontece com as concentra es tanto no ar como na gua.
No ar, o CO2 entra na gua criando uma regi o de baixa concentra o, onde diminui de $C_a$ para $C_{a,0}$. Essa camada tem uma espessura entre 0,1 e 1 mm.
O CO2 que entra na gua se acumula inicialmente na superf cie, criando uma concentra o $C_{w,0}$, que posteriormente difunde para o interior, alcan ando uma concentra o menor $C_w$.
A redu o da concentra o permite definir duas zonas: uma muito fina, de apenas 0,02 a 0,2 mm, onde a concentra o diminui rapidamente, e uma segunda zona de 0,6 a 2 mm, onde a concentra o diminui de forma mais suave at atingir a concentra o no interior da gua.

(ID 12244)
La taxa de transferência de gás na água ($k_w$) pode ser modelada usando dados medidos. Em primeiro lugar, depende da velocidade com que o sistema remove carbono da interface ar- gua, tornando a velocidade de transporte proporcional velocidade relativa entre os dois meios.
Em segundo lugar, h um efeito da mobilidade dos ons, que pode ser descrito por o número Schmidt ($Sc$), representando a rela o entre a difus o de momento e as part culas. No entanto, essa depend ncia n o linear e influenciada por um fator ERROR:9926 que varia entre -1/2 e -2/3 dependendo da rugosidade da superf cie.
Finalmente, la taxa de transferência de gás na água ($k_w$) tamb m depende de ERROR:9409, que por sua vez determinada pelo n vel de rugosidade da superf cie.
Em resumo, o g s la taxa de transferência de gás na água ($k_w$) descrito em fun o de ERROR:9437, ERROR:9408, o número Schmidt ($Sc$), ERROR:9409 e ERROR:9926 da seguinte maneira:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
(ID 15652)
A mobilidade das mol culas, representada por la solubilidade de gás ($\alpha$), uma fun o da concentra o de part culas, descrita por o número Schmidt ($Sc$), que por sua vez calculada a partir de ERROR:9412, ERROR:9413 e ERROR:9414 utilizando a seguinte equa o:
| $ Sc =\displaystyle\frac{ \eta }{ \rho D }$ |
Essa rela o ilustrada no seguinte diagrama:

(ID 12245)
La taxa de transferência de gás no ar ($k_a$) pode ser estimado a partir da lei de Fick, comparando ERROR:9414 com ERROR:9430 da seguinte maneira:
| $ k_a = \displaystyle\frac{ D }{ \delta_c }$ |
(ID 15653)
Para a intera o entre a atmosfera e o oceano, la resistência à transferência de ar para água de um gás ($R_{ta}$) inclui inicialmente la resistência à transferência na água ($R_w$), seguido pelo processo de evapora o $1/\alpha$ com la solubilidade de gás ($\alpha$), e, uma vez que o g s tenha passado para o ar, la resistência de transferência no ar ($R_a$) age sobre ele:
| $ R_{ta} = R_a + \displaystyle\frac{1}{ \alpha } R_w $ |
J para a intera o entre a atmosfera e o oceano, la resistência à transferência de água para ar de um gás ($R_{tw}$) inclui inicialmente la resistência de transferência no ar ($R_a$), seguido de la solubilidade de gás ($\alpha$), e, uma vez que o g s tenha penetrado na gua, age la resistência à transferência na água ($R_w$):
| $ R_{tw} = R_w + \alpha R_a $ |
Com essas equa es, podemos formular as equa es para as velocidades de transfer ncia.
Assim, utilizando la taxa total de transferência de gás no ar ($k_{ta}$), la taxa de transferência de gás na água ($k_w$), la taxa de transferência de gás no ar ($k_a$) e la solubilidade de gás ($\alpha$), estabelecemos a seguinte rela o:
| $ \displaystyle\frac{1}{ k_{ta} } = \displaystyle\frac{1}{ k_a } + \displaystyle\frac{1}{ \alpha k_w } $ |
Por outro lado, com la taxa total de transferência de gás na água ($k_{tw}$), la taxa de transferência de gás na água ($k_w$), la taxa de transferência de gás no ar ($k_a$) e la solubilidade de gás ($\alpha$), estabelecemos que:
| $ \displaystyle\frac{1}{ k_{tw} } = \displaystyle\frac{1}{ k_w } + \displaystyle\frac{ \alpha }{ k_a } $ |
(ID 15654)
(ID 15645)
ID:(1633, 0)
