mechanisms

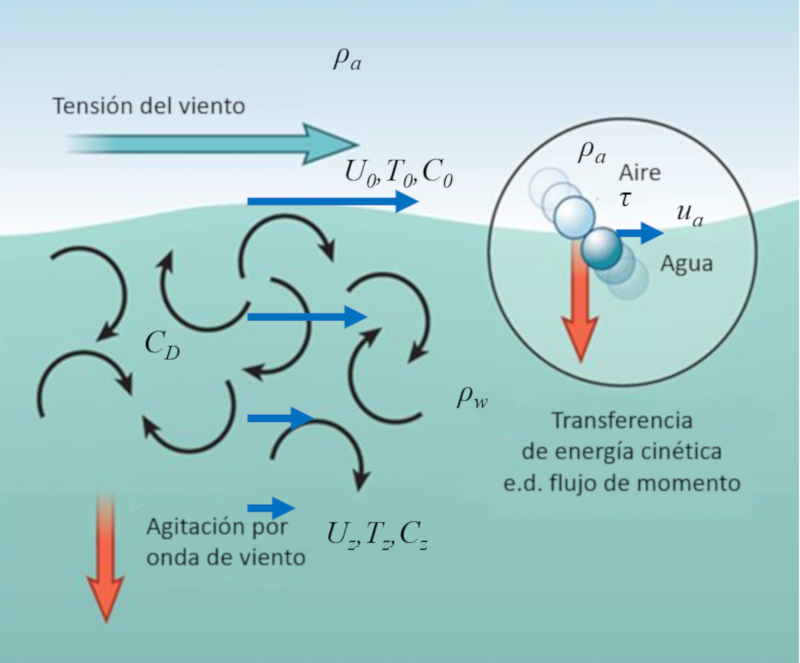
O vento sobre a superf cie do oceano composto por um grande n mero de mol culas que periodicamente colidem com as mol culas de gua na superf cie.

Dessa forma, parte da energia cin tica das mol culas de ar transferida para as mol culas de gua, o que pode ser representado como uma tens o exercida pelo ar sobre a gua.

image

O efeito resultante a cria o de redemoinhos superficiais que, por sua vez, afetam camadas mais profundas, transferindo a velocidade do vento para uma camada superficial do oceano. Isso permite que a energia do vento seja transferida para uma camada pr xima superf cie do oceano, aumentando a velocidade da gua nessa regi o.

Geralmente, ao observar o oceano, diversos mecanismos de gera o de v rtices e turbul ncias s o evidentes, contribuindo para os processos de mistura.

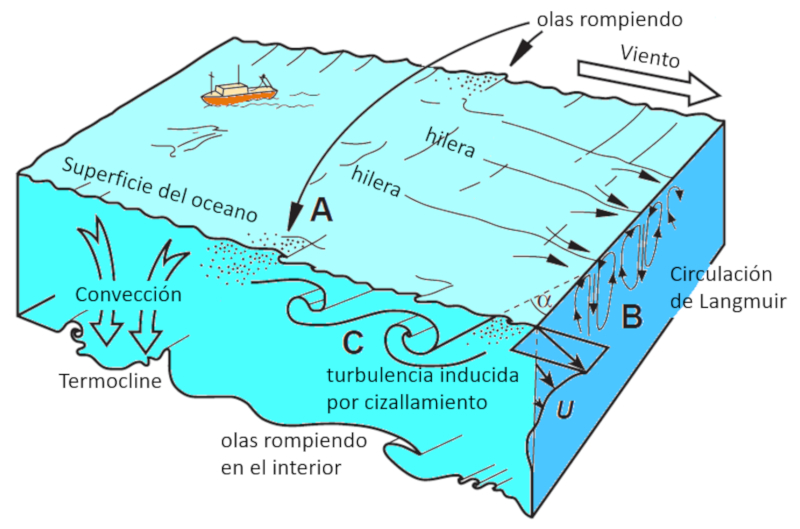
Dentro da camada superficial, destacam-se:

• Ondas superficiais geradas pelos ventos.
• A circula o de Langmuir, que forma fileiras vis veis do ar.
• O rompimento das ondas superficiais.

Enquanto isso, entre o limite inferior da camada de mistura e a termoclina, caracter sticas importantes incluem:

• Turbul ncias devido ao cisalhamento no limite superior.
• Ondas internas quebrando no limite inferior.
• Convec o.
• Instabilidades verticais.

Esses fen menos s o representados no seguinte diagrama:

image

Um dos fen menos originados pelas correntes superficiais induzidas pelo vento a chamada circula o de Langmuir:

image

Essa circula o se origina de forma semelhante ao transporte de Ekman, em que devido for a de Coriolis, h zonas de afundamento que, ao se afundarem, geram bolhas. A circula o se fecha, criando uma zona de surg ncia:

image

No artigo citado na pr xima imagem, conclui-se que existem condi es para a forma o da circula o de Langmuir, as quais dependem das condi es e da pr pria oscila o.

model

A for a ERROR:9433 exercida sobre a superf cie pode ser modelada de acordo com a teoria da similaridade de Monin-Obukhov (MOST) como a transfer ncia de energia cin tica do ar para a camada superior do oceano.

Para isso, assume-se que ERROR:9433 proporcional a ERROR:9418 e diferen a ao quadrado entre ERROR:9408 e ERROR:9437. A proporcionalidade considerada pela introdu o de ERROR:9419, o que leva seguinte conclus o:

kyon

O modelo de Teoria da Similaridade de Monin-Obukhov (MOST) modela a tens o superficial proporcional ao quadrado de ERROR:9408 na superf cie e a la densidade do ar ($\rho_a$).

Neste caso, estima-se a fra o superficial atrav s da densidade de energia cin tica, que se correlaciona com a tens o superficial.

Portanto, estima-se que ERROR:9408 seja

kyon

O termo ERROR:9417 inclui ERROR:9433, ERROR:9434 e ERROR:9435. Portanto, pode ser expresso como:

kyon

Se assumirmos que h uma transi o cont nua na densidade de energia na interface entre o ar e a gua, e considerarmos que essa energia de natureza cin tica, ent o com la densidade do ar ($\rho_a$), ERROR:9408 e ERROR:9438, ERROR:9437 podemos estabelecer a seguinte rela o:

$\rho_a u_a^2=\rho_w u_w^2$

Portanto, podemos estabelecer a rela o:

kyon

Al m disso, podemos considerar que a densidade de energia tem a mesma unidade que a tens o superficial, o que explica a igualdade em fun o de que, em um sistema em equil brio, as tens es devem ser iguais.

Die Beziehung zwischen ERROR:9408 und ERROR:9437 wird durch ERROR:9439 untersucht. Daher kann die Langmuir-Zahl als das Verh ltnis der Quadratwurzel beider Geschwindigkeiten definiert werden:

kyon

O par metro do g s la taxa de transferência de gás na água ($k_w$) descrito em termos de ERROR:9437, ERROR:9408, o número Schmidt ($Sc$), ERROR:9409 e ERROR:9926 da seguinte forma:

kyon