Utilizador:
Elementos de uma geladeira
Definição 
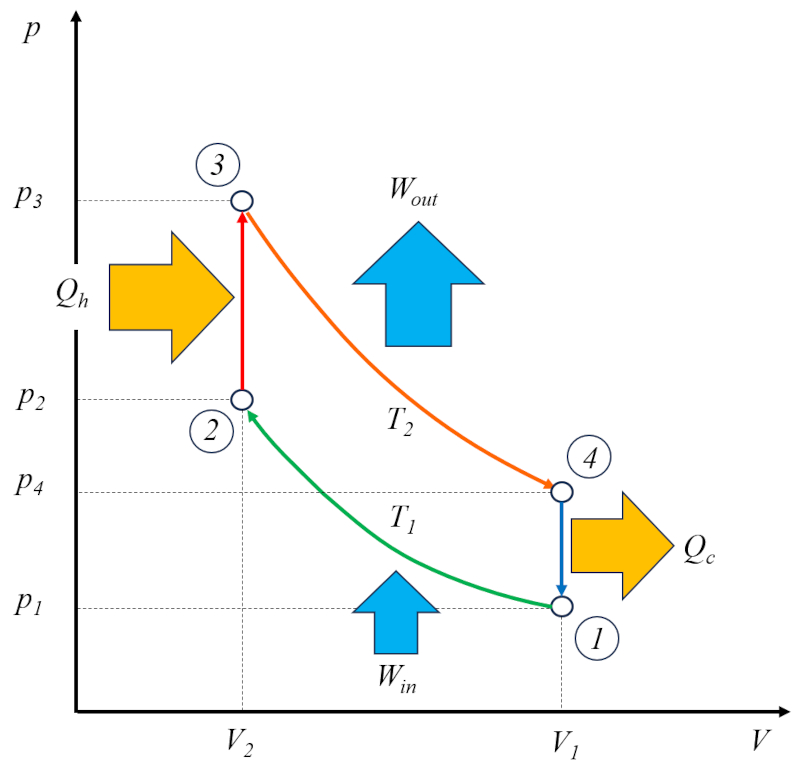
O motor Otto opera em dois ciclos: o ciclo Otto propriamente dito, que consiste nas seguintes fases:
• Fase 1 para 2: Compressão adiabática
• Fase 2 para 3: Aquecimento
• Fase 3 para 4: Expansão adiabática
• Fase 4 para 1: Resfriamento
Além disso, ele possui um ciclo para esvaziar os gases queimados e preencher com uma nova mistura.
Por essa razão, ele é chamado de motor de dois tempos. A fase de esvaziamento e preenchimento pode ser realizada usando uma massa de compensação ou por meio de um segundo cilindro que opera fora de fase.
A eficiência la eficiência ($\eta$) do motor pode ser estimada usando o fator de compressibilidade Otto ($r$) e o índice adiabático ($\kappa$) com a seguinte equação:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(11142, 0)
Motores de combustão
Storyboard
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
A expans o adiab tica descrita usando as vari veis o índice adiabático ($\kappa$), la temperatura no estado 4 ($T_4$), la temperatura no estado 3 ($T_3$), o volume expandido ($V_1$) e o volume compactado ($V_2$) atrav s da rela o
Enquanto a compress o adiab tica representada por la temperatura no estado 1 ($T_1$) e la temperatura no estado 2 ($T_2$) atrav s da rela o
Subtraindo a segunda equa o da primeira, obtemos
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
O que nos leva rela o
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
E isso nos permite definir o fator de compressibilidade Otto ($r$) da seguinte forma:
La eficiência ($\eta$), em termos de la temperatura no estado 1 ($T_1$), la temperatura no estado 2 ($T_2$), la temperatura no estado 3 ($T_3$) e la temperatura no estado 4 ($T_4$), calculado usando a seguinte equa o:
No caso de expans o adiab tica, ela descrita usando o índice adiabático ($\kappa$), o volume expandido ($V_1$) e o volume compactado ($V_2$) com a rela o:
E a compress o adiab tica representada pela rela o:
Se subtrairmos a segunda equa o da primeira, obtemos:
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
O que nos leva rela o:
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Isso, por sua vez, leva defini o de o fator de compressibilidade Otto ($r$) com a seguinte equa o:
Com todos esses componentes, a efici ncia de um processo usando o ciclo Otto pode ser calculada como:
Exemplos
O motor Otto opera em dois ciclos: o ciclo Otto propriamente dito, que consiste nas seguintes fases:
• Fase 1 para 2: Compress o adiab tica
• Fase 2 para 3: Aquecimento
• Fase 3 para 4: Expans o adiab tica
• Fase 4 para 1: Resfriamento
Al m disso, ele possui um ciclo para esvaziar os gases queimados e preencher com uma nova mistura.
Por essa raz o, ele chamado de motor de dois tempos. A fase de esvaziamento e preenchimento pode ser realizada usando uma massa de compensa o ou por meio de um segundo cilindro que opera fora de fase.
A efici ncia la eficiência ($\eta$) do motor pode ser estimada usando o fator de compressibilidade Otto ($r$) e o índice adiabático ($\kappa$) com a seguinte equa o:
La eficiência ($\eta$) , em ltima inst ncia, uma fun o de o volume expandido ($V_1$) e o volume compactado ($V_2$), e em particular, de o fator de compressibilidade Otto ($r$):
La eficiência ($\eta$) pode ser calculado a partir de o fator de compressibilidade Otto ($r$) e o índice adiabático ($\kappa$) no caso do ciclo Otto usando:
ID:(1677, 0)