Usuario:
Solución técnica
Imagen 
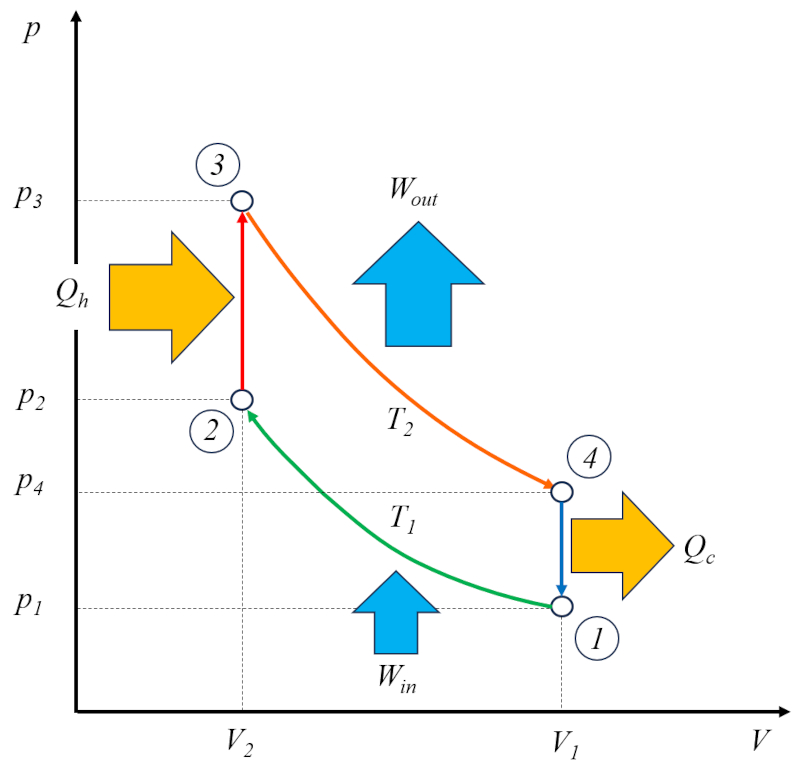
El motor de Otto opera en dos ciclos: el ciclo de Otto propiamente dicho, que consta de las siguientes fases:
• Fase 1 a 2: Compresión adiabática
• Fase 2 a 3: Calentamiento
• Fase 3 a 4: Expansión adiabática
• Fase 4 a 1: Enfriamiento
Además, tiene un ciclo de vaciado de los gases quemados y llenado con una mezcla nueva.
Por esta razón, se le llama un motor de dos tiempos. La fase de vaciado y llenado se puede llevar a cabo mediante una masa de compensación o a través de un segundo cilindro que opera desfasado.
La eficiencia la eficiencia ($\eta$) del motor se puede estimar utilizando el factor de compresibilidad de Otto ($r$) y el indice adiabático ($\kappa$) con la siguiente ecuación:
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(11142, 0)
Motores a combustión
Storyboard
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
La expansi n adiab tica se describe utilizando las variables el indice adiabático ($\kappa$), la temperatura en estado 4 ($T_4$), la temperatura en estado 3 ($T_3$), el volumen expandido ($V_1$) y el volumen comprimido ($V_2$), a trav s de la relaci n
Mientras que la compresi n adiab tica se representa con la temperatura en estado 1 ($T_1$) y la temperatura en estado 2 ($T_2$) mediante la relaci n
Al restar la segunda ecuaci n de la primera, obtenemos
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Lo que nos lleva a la relaci n
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Y esto nos permite definir el factor de compresibilidad de Otto ($r$) de la siguiente manera:
La eficiencia ($\eta$), en funci n de la temperatura en estado 1 ($T_1$), la temperatura en estado 2 ($T_2$), la temperatura en estado 3 ($T_3$) y la temperatura en estado 4 ($T_4$), se calcula mediante la ecuaci n:
En el caso de una expansi n adiab tica, se describe con el indice adiabático ($\kappa$), el volumen expandido ($V_1$) y el volumen comprimido ($V_2$) mediante la relaci n:
Mientras que la compresi n adiab tica se representa mediante la relaci n:
Si restamos la segunda ecuaci n de la primera, obtenemos:
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Lo cual nos lleva a la relaci n:
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Esto, a su vez, conduce a la definici n de el factor de compresibilidad de Otto ($r$) mediante la ecuaci n:
Con todos estos elementos, el rendimiento de un proceso utilizando el ciclo de Otto se puede calcular de la siguiente manera:
Ejemplos
El motor de Otto opera en dos ciclos: el ciclo de Otto propiamente dicho, que consta de las siguientes fases:
• Fase 1 a 2: Compresi n adiab tica
• Fase 2 a 3: Calentamiento
• Fase 3 a 4: Expansi n adiab tica
• Fase 4 a 1: Enfriamiento
Adem s, tiene un ciclo de vaciado de los gases quemados y llenado con una mezcla nueva.
Por esta raz n, se le llama un motor de dos tiempos. La fase de vaciado y llenado se puede llevar a cabo mediante una masa de compensaci n o a trav s de un segundo cilindro que opera desfasado.
La eficiencia la eficiencia ($\eta$) del motor se puede estimar utilizando el factor de compresibilidad de Otto ($r$) y el indice adiabático ($\kappa$) con la siguiente ecuaci n:
La eficiencia ($\eta$) es en ltima instancia una funci n dependiente de el volumen expandido ($V_1$) y el volumen comprimido ($V_2$), y espec ficamente, de el factor de compresibilidad de Otto ($r$):
La eficiencia ($\eta$) se puede calcular de el factor de compresibilidad de Otto ($r$) y el indice adiabático ($\kappa$) en el caso del ciclo de Otto mediante:
ID:(1677, 0)