Utilisateur:
Éléments d'un réfrigérateur
Définition 
Le moteur Otto fonctionne selon deux cycles : le cycle Otto proprement dit, qui comprend les phases suivantes :
• Phase 1 à 2 : Compression adiabatique
• Phase 2 à 3 : Chauffage
• Phase 3 à 4 : Expansion adiabatique
• Phase 4 à 1 : Refroidissement
De plus, il possède un cycle pour vider les gaz brûlés et les remplir d'un nouveau mélange.
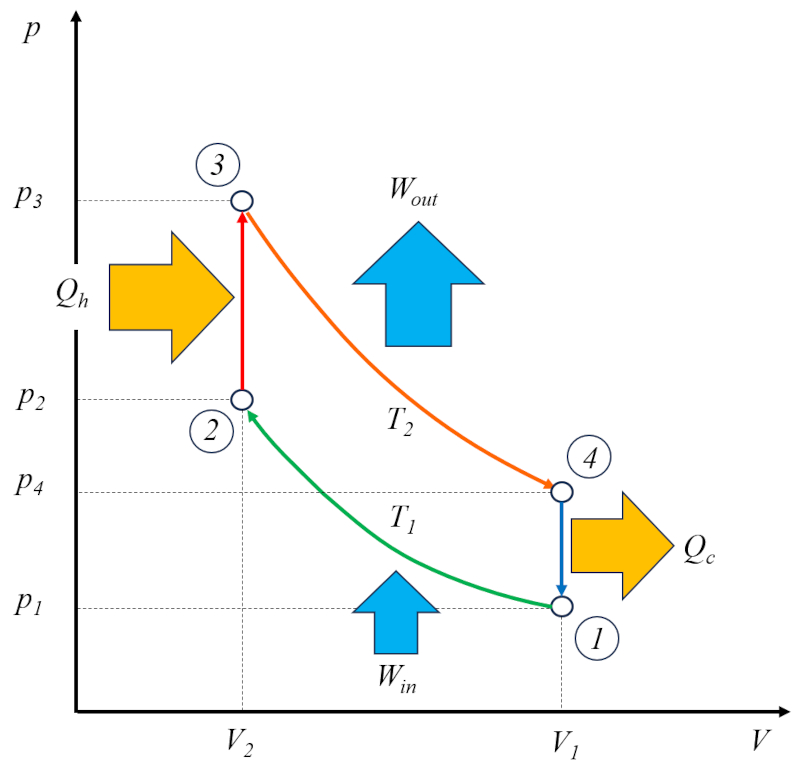
Pour cette raison, il est appelé un moteur deux temps. La phase de vidange et de remplissage peut être réalisée à l'aide d'une masse de compensation ou par le biais d'un second cylindre qui fonctionne en déphasage.
L'efficacité A efficacité ($\eta$) du moteur peut être estimée en utilisant le facteur de compressibilité Otto ($r$) et le indice adiabatique ($\kappa$) avec l'équation suivante :
| $ \eta = 1-\displaystyle\frac{1}{ r ^{ \kappa -1}}$ |
ID:(11142, 0)
Moteurs à combustion
Storyboard
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
L'expansion adiabatique est d crite l'aide des variables le indice adiabatique ($\kappa$), a température à l'état 4 ($T_4$), a température à l'état 3 ($T_3$), le volume étendu ($V_1$) et le volume compressé ($V_2$) travers la relation
Tandis que la compression adiabatique est repr sent e par a température à l'état 1 ($T_1$) et a température à l'état 2 ($T_2$) travers la relation
En soustrayant la deuxi me quation de la premi re, nous obtenons
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Ce qui nous conduit la relation
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Et cela nous permet de d finir le facteur de compressibilité Otto ($r$) de la mani re suivante :
A efficacité ($\eta$), en fonction de a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$), est calcul l'aide de l' quation suivante :
Dans le cas de l'expansion adiabatique, elle est d crite l'aide de le indice adiabatique ($\kappa$), le volume étendu ($V_1$) et le volume compressé ($V_2$) avec la relation suivante :
Et la compression adiabatique est repr sent e par la relation suivante :
Si nous soustrayons la deuxi me quation de la premi re, nous obtenons :
$(T_4 - T_1)V_1^{\kappa-1} = (T_3 - T_2)V_2^{\kappa-1}$
Ce qui nous conduit la relation :
$\left(\displaystyle\frac{V_1}{V_2}\right)^{\kappa-1} = \displaystyle\frac{T_3 - T_2}{T_4 - T_1}$
Cela nous conduit la d finition de le facteur de compressibilité Otto ($r$) avec l' quation suivante :
Avec tous ces composants, l'efficacit d'un processus utilisant le cycle Otto peut tre calcul e comme suit :
Exemples
Le moteur Otto fonctionne selon deux cycles : le cycle Otto proprement dit, qui comprend les phases suivantes :
• Phase 1 2 : Compression adiabatique
• Phase 2 3 : Chauffage
• Phase 3 4 : Expansion adiabatique
• Phase 4 1 : Refroidissement
De plus, il poss de un cycle pour vider les gaz br l s et les remplir d'un nouveau m lange.
Pour cette raison, il est appel un moteur deux temps. La phase de vidange et de remplissage peut tre r alis e l'aide d'une masse de compensation ou par le biais d'un second cylindre qui fonctionne en d phasage.
L'efficacit a efficacité ($\eta$) du moteur peut tre estim e en utilisant le facteur de compressibilité Otto ($r$) et le indice adiabatique ($\kappa$) avec l' quation suivante :
A efficacité ($\eta$) est finalement une fonction de le volume étendu ($V_1$) et le volume compressé ($V_2$), et en particulier, de le facteur de compressibilité Otto ($r$) :
A efficacité ($\eta$) peut tre calcul partir de le facteur de compressibilité Otto ($r$) et le indice adiabatique ($\kappa$) dans le cas du cycle d'Otto en utilisantxa0:
ID:(1677, 0)