Usuario:
Deformación elástica
Nota 
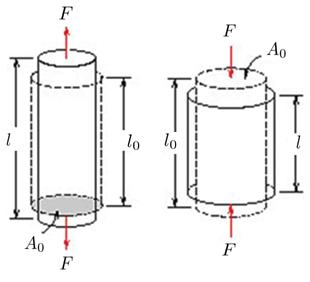
Bajo pequeñas cargas el cuerpo se deforma sin que los átomos sufran desplazamientos relativos:
ID:(12889, 0)
Deformación plástica
Cita
Si se aumenta la deformación comienzan a ocurrir desplazamientos físicos de los átomos que modifican la estructura original:
ID:(12887, 0)
Coeficiente de fricción
Ecuación
La fuerza de fricción se compone de
- La adhesión de la superficie $S$ del arado al suelo por efecto de la tensión superficial del agua contenida en este
- El roce por el desplazamiento que aumenta con la humedad por el efecto de aumento de la adhesión por efecto del agua. Pasado un cierto nivel vuelve a decrecer por el efecto lubricante de este.
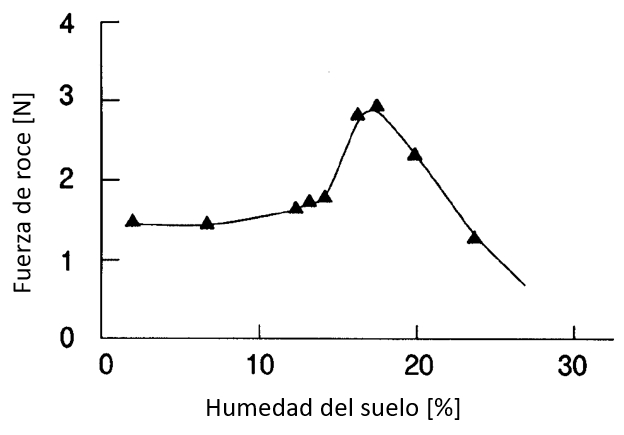
El coeficiente de roce varia con la humedad del suelo de la forma como se muestra
ID:(12886, 0)
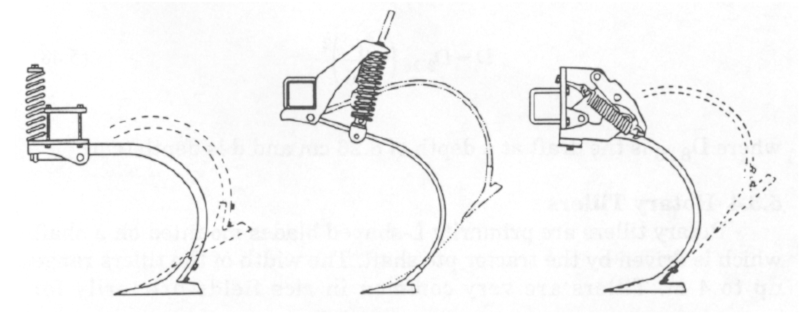
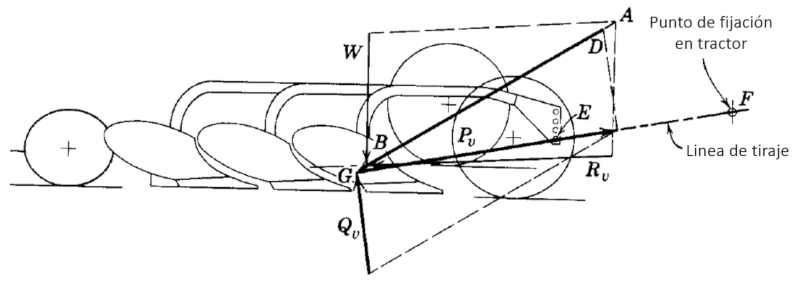
Arado
Storyboard
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Con la Ley de Hooke para la fuerza elástica ($F_k$), la constante de Hooke ($k$) y la elongación ($u$) de la siguiente forma:
y la expresi n para la constante de Hooke ($k$) en funci n de el largo del cuerpo ($L$), la sección del elemento ($S$), el largo del resorte microscópico ($l$), la sección del resorte microscópico ($s$) y la constante de Hook microscópica ($k_m$):
combinada con la expresi n para el módulo de Elasticidad ($E$):
el resultado es:
Ejemplos
Deformaci n lateral
Ya que la Ley de Hooke relaciona la fuerza elástica ($F_k$) a trav s de la constante de Hooke ($k$) y la elongación ($u$) de la manera siguiente:
es posible sustituir la constante de Hooke ($k$) por la expresi n microsc pica y utilizando la definici n de el módulo de Elasticidad ($E$), se obtiene con el largo del cuerpo ($L$) y la sección del elemento ($S$) que:
La fuerza elástica ($F_k$) es una funci n que depende de el módulo de Elasticidad ($E$), la sección del elemento ($S$), la elongación ($u$) y el largo del cuerpo ($L$).
De manera similar, al igual que se introduce la deformación ($\epsilon$) para evitar el uso de la dimensi n el largo del cuerpo ($L$), podemos construir un factor que exprese la fuerza elástica ($F_k$) en funci n de la sección del elemento ($S$) como la tensión ($\sigma$).
El comportamiento el stico
La constante de proporcionalidad entre tensi n y deformaci n se denomina el modulo de elasticidad y se denota por la letra
Por ello se tiene que
El modulo de elasticidad depende del material siendo en el caso del suelo relativamente bajo
La deformaci n lateral es directamente proporcional a la deformaci n que la causa. El coeficiente de proporcionalidad se denota como el coeficiente de Poisson ($\nu$) [1] y generalmente cae en el rango de 0.15 a 0.4.
Si la deformaci n original es la deformación ($\epsilon$) y la generada es la deformación en la dirección perpendicular a la fuerza ($\epsilon_{\perp}$), se establece la siguiente relaci n:
En la aproximaci n lineal, el coeficiente de Poisson representa la relaci n entre las deformaciones lateral y longitudinal.
donde el signo indica que la deformaci n es en direcci n opuesta a la que la causa.
[1] Este concepto fue introducido por Sim on Denis Poisson en un trabajo de an lisis estad stico en el que, entre otros temas no relacionados con la mec nica, menciona lo que posteriormente se denomin coeficiente de Poisson en un ejemplo de elasticidad. El trabajo se titula "Recherches sur la Probabilit des Jugements en Mati re Criminelle et en Mati re Civile" (Investigaciones sobre la Probabilidad de los Juicios en Materias Criminales y Civiles), escrito por Sim on Denis Poisson (1837).
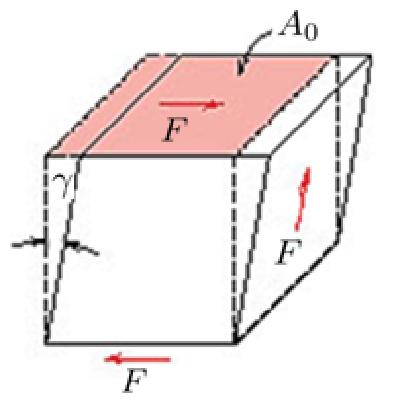
Deformaci n tipo Cizalla
Bajo peque as cargas el cuerpo se deforma sin que los tomos sufran desplazamientos relativos:
Si se aumenta la deformaci n comienzan a ocurrir desplazamientos f sicos de los tomos que modifican la estructura original:
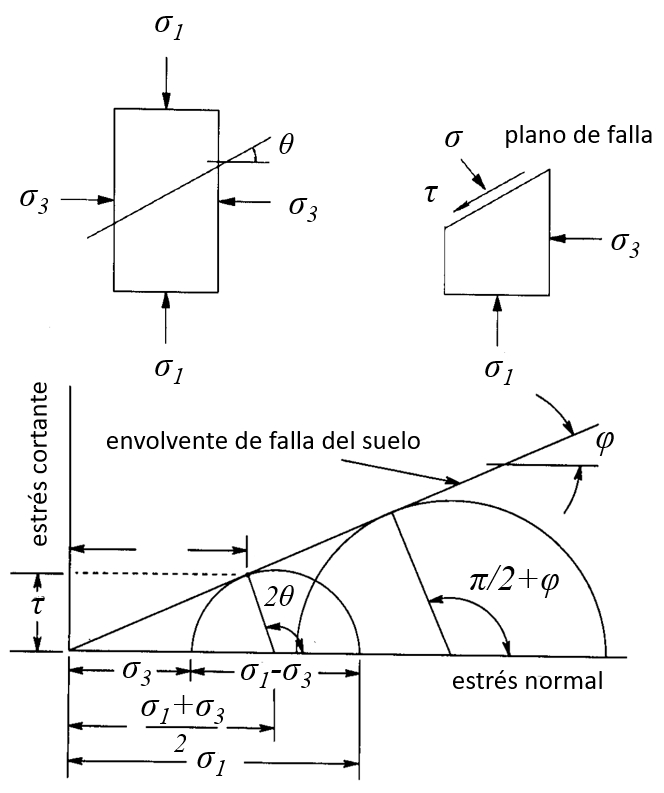
La tensi n normal se puede calcular de las tensiones en el eje vertical
La cizalla se puede calcular de las tensiones en el eje vertical
La envolvente limite de Mohr se puede expresar como una ecuaci n de la forma
con
La fuerza de fricci n se compone de
- La adhesi n de la superficie $S$ del arado al suelo por efecto de la tensi n superficial del agua contenida en este
- El roce por el desplazamiento que aumenta con la humedad por el efecto de aumento de la adhesi n por efecto del agua. Pasado un cierto nivel vuelve a decrecer por el efecto lubricante de este.
La ecuaci n que lo representa se puede escribir como
con
La fuerza de fricci n se compone de
- La adhesi n de la superficie $S$ del arado al suelo por efecto de la tensi n superficial del agua contenida en este
- El roce por el desplazamiento que aumenta con la humedad por el efecto de aumento de la adhesi n por efecto del agua. Pasado un cierto nivel vuelve a decrecer por el efecto lubricante de este.
El coeficiente de roce varia con la humedad del suelo de la forma como se muestra
ID:(1681, 0)