User:
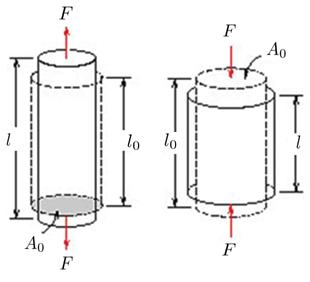
Deformación elástica
Note 
Bajo pequeñas cargas el cuerpo se deforma sin que los átomos sufran desplazamientos relativos:
ID:(12889, 0)
Deformación plástica
Quote
Si se aumenta la deformación comienzan a ocurrir desplazamientos físicos de los átomos que modifican la estructura original:
ID:(12887, 0)
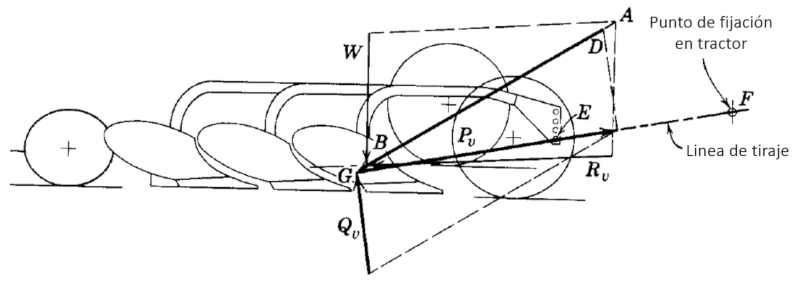
Coeficiente de fricción
Equation
La fuerza de fricción se compone de
- La adhesión de la superficie $S$ del arado al suelo por efecto de la tensión superficial del agua contenida en este
- El roce por el desplazamiento que aumenta con la humedad por el efecto de aumento de la adhesión por efecto del agua. Pasado un cierto nivel vuelve a decrecer por el efecto lubricante de este.
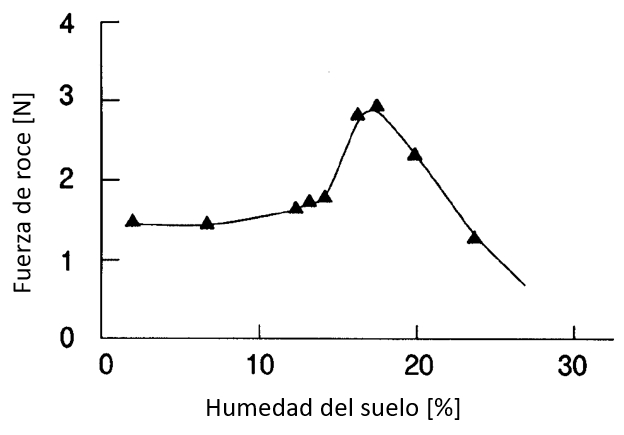
El coeficiente de roce varia con la humedad del suelo de la forma como se muestra
ID:(12886, 0)
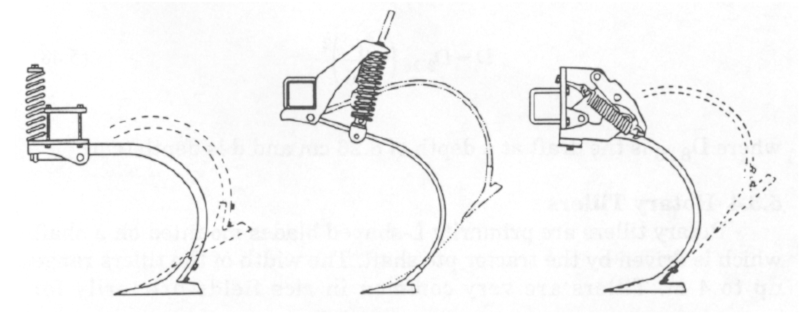
Plow
Storyboard
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
With Hooke's Law for the elastic Force ($F_k$), the hooke Constant ($k$), and the elongation ($u$) as follows:
and the expression for the hooke Constant ($k$) in terms of the body length ($L$), the body Section ($S$), the microscopic length of spring ($l$), the microscopic section of spring ($s$), and the microscopic Hook constant ($k_m$):
combined with the expression for the modulus of Elasticity ($E$):
the result is:
Examples
Deformaci n lateral
As Hooke's Law relates the elastic Force ($F_k$) through the hooke Constant ($k$) and the elongation ($u$) in the following manner:
you can replace the hooke Constant ($k$) with the microscopic expression and using the definition of the modulus of Elasticity ($E$), you obtain with the body length ($L$) and the body Section ($S$) that:
The elastic Force ($F_k$) is a function that depends on the modulus of Elasticity ($E$), the body Section ($S$), the elongation ($u$), and the body length ($L$).
Similarly, just as the deformation ($\epsilon$) is introduced to avoid using the dimension the body length ($L$), we can construct a factor that expresses the elastic Force ($F_k$) in terms of the body Section ($S$) as the strain ($\sigma$).
Lateral deformation is directly proportional to the deformation it causes. The proportionality coefficient is denoted as the poisson coefficient ($\nu$) [1] and typically falls within the range of 0.15 to 0.4.
If the original deformation is the deformation ($\epsilon$) and the generated one is the deformation in the direction perpendicular to the force ($\epsilon_{\perp}$), the following relationship is established:
In the linear approximation, the Poisson's coefficient represents the relationship between lateral and longitudinal deformations.
where the sign indicates that the deformation is in the opposite direction to the cause.
[1] This concept was introduced by Sim on Denis Poisson in a statistical analysis work, in which he mentioned, among other unrelated topics to mechanics, what was later referred to as the Poisson's coefficient in an elasticity example. The work is titled "Recherches sur la Probabilit des Jugements en Mati re Criminelle et en Mati re Civile" (Research on the Probability of Judgments in Criminal and Civil Matters), authored by Sim on Denis Poisson (1837).
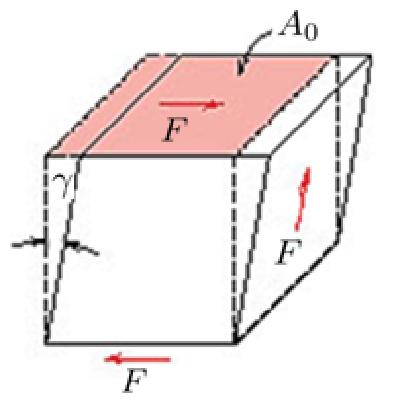
Deformaci n tipo Cizalla
Bajo peque as cargas el cuerpo se deforma sin que los tomos sufran desplazamientos relativos:
Si se aumenta la deformaci n comienzan a ocurrir desplazamientos f sicos de los tomos que modifican la estructura original:
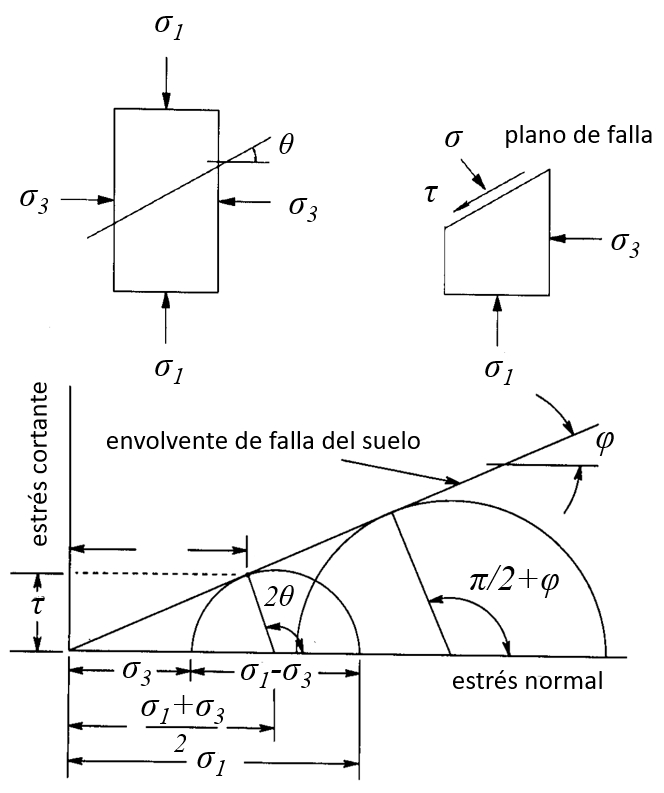
La tensi n normal se puede calcular de las tensiones en el eje vertical
La cizalla se puede calcular de las tensiones en el eje vertical
La envolvente limite de Mohr se puede expresar como una ecuaci n de la forma
con
La fuerza de fricci n se compone de
- La adhesi n de la superficie $S$ del arado al suelo por efecto de la tensi n superficial del agua contenida en este
- El roce por el desplazamiento que aumenta con la humedad por el efecto de aumento de la adhesi n por efecto del agua. Pasado un cierto nivel vuelve a decrecer por el efecto lubricante de este.
La ecuaci n que lo representa se puede escribir como
con
La fuerza de fricci n se compone de
- La adhesi n de la superficie $S$ del arado al suelo por efecto de la tensi n superficial del agua contenida en este
- El roce por el desplazamiento que aumenta con la humedad por el efecto de aumento de la adhesi n por efecto del agua. Pasado un cierto nivel vuelve a decrecer por el efecto lubricante de este.
El coeficiente de roce varia con la humedad del suelo de la forma como se muestra
ID:(1681, 0)