Utilisateur:
Éclairage
Storyboard 
Une fois que l'éclairage naturel a été évalué, il est possible de déterminer la quantité de lumière additionnelle qui peut être nécessaire pendant la journée et de concevoir le système d'éclairage en conséquence. De plus, il est important de calculer la quantité de lumière requise pour les moments où la lumière naturelle n'est pas disponible.
ID:(2093, 0)
Modèle de gaz photonique
Concept
Un modèle simple pour étudier l'éclairage nécessaire est celui d'un gaz de photons occupant le volume de la pièce. Ces particules pénètrent dans la pièce par les fenêtres depuis l'extérieur et/ou par les lampes à l'intérieur de la pièce :
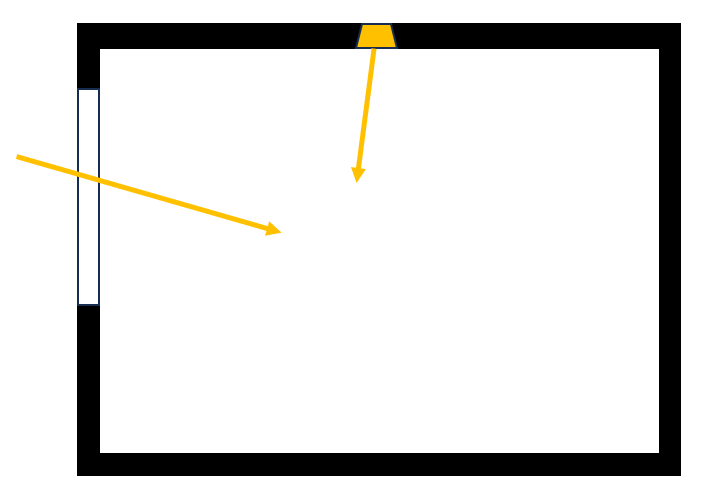
Les photons se déplacent à A surface de la fontaine ($c$) à travers l'espace, frappant les murs, où seule une fraction correspondant à Le albédo ($a$) est réfléchie. La fraction $1-a$ est absorbée par les surfaces, et ainsi les photons quittent le système :
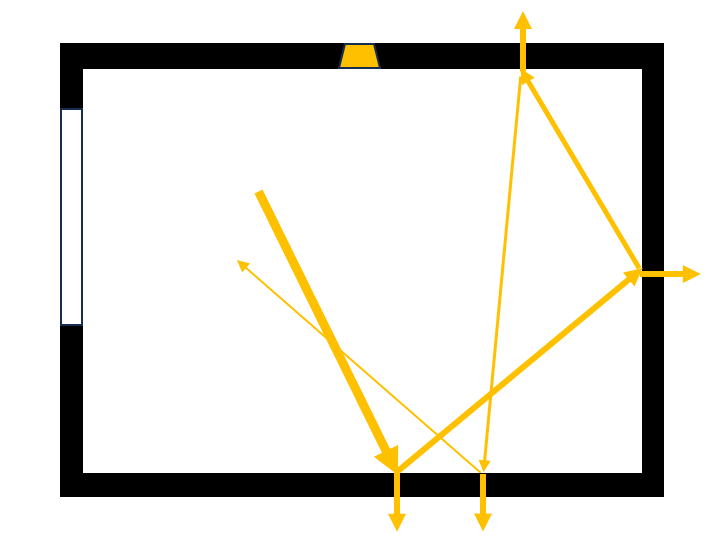
Étant donné que les murs ne sont pas parfaitement lisses, la lumière se réfléchit de manière isotrope, c'est-à-dire sans privilégier une direction particulière. Finalement, il y a un flux entrant de photons à travers les fenêtres et/ou les lampes, et un flux dominant d'absorption par les murs, qui, dans une situation d'équilibre, sera égal au flux entrant :
ID:(137, 0)
Concentration de photons de référence
Concept
La quantité de lumière, représentée par le nombre de photons entrant dans la pièce par unité de temps, que ce soit par les fenêtres ou les lampes, peut être estimée à l'aide des variables a intensité ($I$) et surface de la fontaine ($S_w$), en considérant que chaque photon possède une énergie de a fréquence lumineuse ($\epsilon$). Cette relation est donnée par la formule suivante :
$\displaystyle\frac{I S_w}{\epsilon}$
Celle-ci est illustrée dans le graphique suivant :
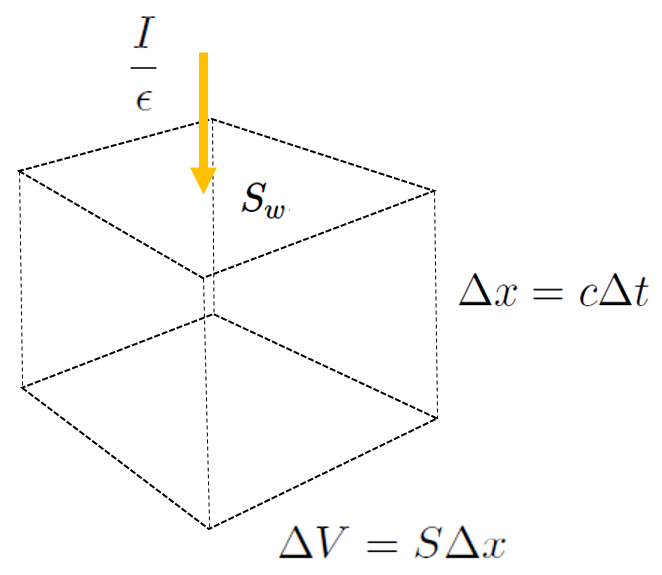
Les photons qui pénètrent dans l'espace sont perdus en raison de l'absorption par les surfaces des murs, du plafond et du sol, selon la valeur surfaces murales ($S$). Le nombre de photons qui impactent ces surfaces est proportionnel à A concentration de photons ($n$), et la fraction absorbée est le complément de le albédo ($a$). De plus, si la distribution des photons est anisotrope, seulement 1/6 des photons proches de la surface se dirigeront vers celle-ci. Par conséquent, le flux de photons absorbés peut s'exprimer ainsi :
$\displaystyle\frac{1}{6} n S (1-a)$
Cette relation est également représentée dans le graphique suivant :
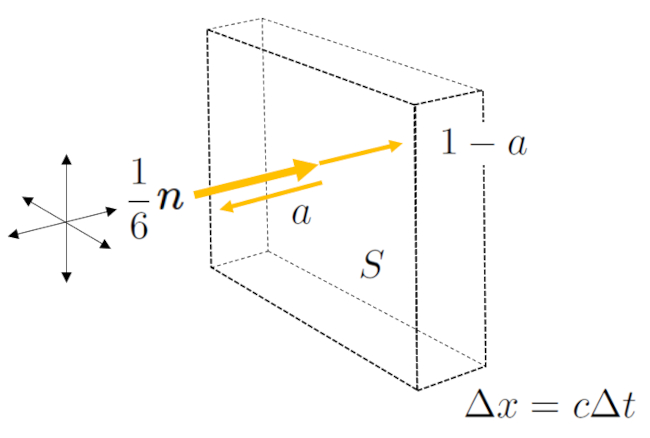
En général, le second flux est inférieur au premier, ce qui implique que le flux entrant est absorbé à travers plusieurs réflexions sur les murs. Cependant, ce processus est si rapide que l'il humain ne peut pas le percevoir, si bien que l'interruption d'une source lumineuse entraîne un obscurcissement apparemment instantané.
ID:(139, 0)
Bilan photonique
Concept
En considérant le flux de photons entrant et celui qui est absorbé, il est possible de calculer comment a concentration de photons ($n$) varie en fonction de le temps ($t$) dans volume d'espace ($V$). Cela est représenté dans le graphique suivant :
indiquant que la variation de a concentration de photons ($n$) par rapport à Le temps ($t$),
$\displaystyle\frac{dn}{dt}$
sera égale au flux entrant :
$\displaystyle\frac{S_w I}{\epsilon V}$
impliquant les variables surface de la fontaine ($S_w$), a intensité ($I$), a fréquence lumineuse ($\epsilon$) et volume d'espace ($V$), moins la perte due à l'absorption par les murs :
$\displaystyle\frac{1}{6}\displaystyle\frac{S (1-a) c n}{V}$
avec les variables a surface de la fontaine ($c$), le albédo ($a$) et surfaces murales ($S$), ce qui donne l'équation suivante :
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
ID:(15869, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ c = \nu \lambda $
c = nu * lambda
$ \epsilon = h \nu $
e = h * nu
$ n = n_a + (n_0 - n_a) e^{- t / \tau }$
n = n_a +( n_0 - n_a )*exp(- t / tau )
$ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$
n_a = 6 * I * S_w /( c *(1- a )* e * S )
$ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$
tau = 6* V /( c *(1 - a )* S )
$\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$
@DIF( n , t , 1) = - c * S *(1- a ) * n /(6* V ) + S_w * I /( e * V )
ID:(15874, 0)
Bilan photonique
Équation
La variation de a concentration de photons ($n$) en fonction de le temps ($t$) est due au flux entrant moins la fraction qui est absorbée. Par conséquent, en utilisant les variables surface de la fontaine ($S_w$), a intensité ($I$), surfaces murales ($S$), le albédo ($a$), volume d'espace ($V$), a surface de la fontaine ($c$) et a fréquence lumineuse ($\epsilon$), on obtient l'équation suivante :
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
La variation de a concentration de photons ($n$) par rapport à Le temps ($t$),
$\displaystyle\frac{dn}{dt}$
sera égale au flux entrant :
$\displaystyle\frac{S_w I}{\epsilon V}$
qui implique les variables surface de la fontaine ($S_w$), a intensité ($I$), a fréquence lumineuse ($\epsilon$) et volume d'espace ($V$), moins la perte due à l'absorption par les murs :
$\displaystyle\frac{1}{6}\displaystyle\frac{S (1-a) c n}{V}$
en utilisant les variables a surface de la fontaine ($c$), le albédo ($a$) et surfaces murales ($S$), ce qui donne l'équation suivante :
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
ID:(15870, 0)
Fréquence et longueur d'onde des Photons
Équation
Le photon est décrit comme une onde, et le fréquence des photons ($\nu$) est liée à ($$) par a surface de la fontaine ($c$), selon la formule suivante :
| $ c = \nu \lambda $ |
Étant donné que le fréquence des photons ($\nu$) est l'inverse de le période ($T$) :
$\nu=\displaystyle\frac{1}{T}$
cela signifie que a surface de la fontaine ($c$) est égal à la distance parcourue en une oscillation, c'est-à-dire ($$), divisée par le temps écoulé, qui correspond à la période :
$c=\displaystyle\frac{\lambda}{T}$
En d'autres termes, la relation suivante s'applique :
| $ c = \nu \lambda $ |
Cette formule correspond à la relation mécanique qui établit que la vitesse de l'onde est égale à la longueur d'onde (distance parcourue) divisée par la période d'oscillation, ou inversement proportionnelle à la fréquence (l'inverse de la période).
ID:(3953, 0)
Énergie photonique
Équation
La couleur de la lumière est associée à sa le fréquence des photons ($\nu$), et il existe une relation directe entre cette fréquence et a fréquence lumineuse ($\epsilon$) :
| $ \epsilon = h \nu $ |
où A constante de Planck ($h$) a une valeur de $6,62\times 10^{-34} , \text{Js}$.
ID:(3341, 0)
Concentration de photons en cas stationnaire
Équation
Dans le cas stationnaire, le nombre de photons entrant dans la pièce est égal au nombre de photons absorbés, ce qui signifie qu'il existe une a concentration asymptotique de photons ($n_a$) qui peut être calculée à partir de surface de la fontaine ($S_w$), a intensité ($I$), surfaces murales ($S$), le albédo ($a$), a surface de la fontaine ($c$) et a fréquence lumineuse ($\epsilon$) à laide de léquation suivante :
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
Le flux de photons dans une pièce est décrit par a concentration de photons ($n$) en fonction de le temps ($t$), en utilisant les variables surface de la fontaine ($S_w$), a intensité ($I$), surfaces murales ($S$), le albédo ($a$), a surface de la fontaine ($c$) et a fréquence lumineuse ($\epsilon$), selon léquation suivante :
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
Dans le cas stationnaire, la dérivée est nulle, et en résolvant léquation pour a concentration de photons ($n$), on peut définir a concentration asymptotique de photons ($n_a$) à laide de la relation suivante :
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
Il est important de garder à lesprit que cela représente un niveau moyen de lumière dans une pièce, qui variera en fonction de lemplacement à lintérieur de celle-ci. Lintensité de la lumière dépendra de la réception de lumière directe de la source ou de multiples réflexions, qui diminuent progressivement, créant des zones où seule une petite quantité de lumière parvient.
ID:(15868, 0)
Temps de relaxation d'absorption
Équation
Avec l'équation de bilan des photons et la concentration stationnaire de photons, on peut déterminer une échelle de temps le temps de détente ($\tau$) qui dépend de volume d'espace ($V$), surfaces murales ($S$), le albédo ($a$) et a surface de la fontaine ($c$) via :
| $ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$ |
Comme la variation de a concentration de photons ($n$) en fonction de le temps ($t$) est due au flux entrant moins la fraction absorbée, l'équation peut être exprimée en utilisant les variables surface de la fontaine ($S_w$), a intensité ($I$), surfaces murales ($S$), le albédo ($a$), volume d'espace ($V$), a surface de la fontaine ($c$) et a fréquence lumineuse ($\epsilon$), ce qui donne l'équation suivante :
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
Avec la relation pour a concentration asymptotique de photons ($n_a$) donnée par :
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
l'équation peut être réécrite comme suit :
$\displaystyle\frac{dn}{dt} = \displaystyle\frac{1}{\tau}(n_0-n)$
où Le temps de détente ($\tau$) est :
| $ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$ |
ID:(15872, 0)
Evolution temporelle de la concentration de photons
Équation
En résolvant léquation de bilan des photons, on obtient que a concentration de photons ($n$) en fonction de le temps ($t$), avec les variables le concentration initiale ($n_0$), a concentration asymptotique de photons ($n_a$) et le temps de détente ($\tau$), est :
| $ n = n_a + (n_0 - n_a) e^{- t / \tau }$ |
Comme la variation de a concentration de photons ($n$) en fonction de le temps ($t$) est due au flux entrant moins la fraction absorbée, l'équation peut être exprimée en utilisant les variables surface de la fontaine ($S_w$), a intensité ($I$), surfaces murales ($S$), le albédo ($a$), volume d'espace ($V$), a surface de la fontaine ($c$) et a fréquence lumineuse ($\epsilon$), ce qui donne la relation suivante :
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
Avec la relation pour a concentration asymptotique de photons ($n_a$) donnée par :
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
et avec le temps de détente ($\tau$) :
| $ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$ |
l'équation peut être réécrite comme suit :
$\displaystyle\frac{dn}{dt} = \displaystyle\frac{1}{\tau}(n_0-n)$
dont la solution est :
| $ n = n_a + (n_0 - n_a) e^{- t / \tau }$ |
avec le concentration initiale ($n_0$).
ID:(15871, 0)