User:
Lightning
Storyboard 
Once natural lighting has been assessed, it's possible to determine the amount of additional lighting that may be needed during the day and design the lighting system accordingly. Additionally, it's important to calculate the amount of lighting required for times when natural light is not available.
ID:(2093, 0)
Photon gas model
Concept
A simple model to study the required lighting is that of a photon gas occupying the volume of the room. These particles enter the room through the windows from outside and/or from lamps inside the room:
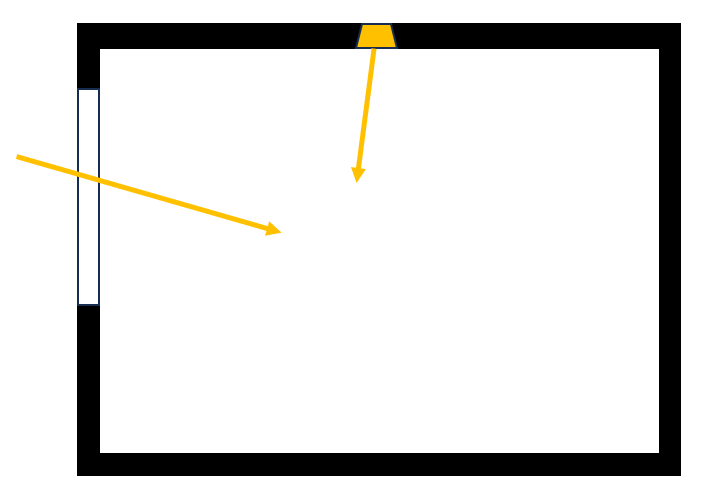
None
The photons move at the speed of Light ($c$) across the space, hitting the walls, where only a fraction corresponding to the albedo ($a$) is reflected. The fraction $1-a$ is absorbed by the walls, and thus the photons exit the system:
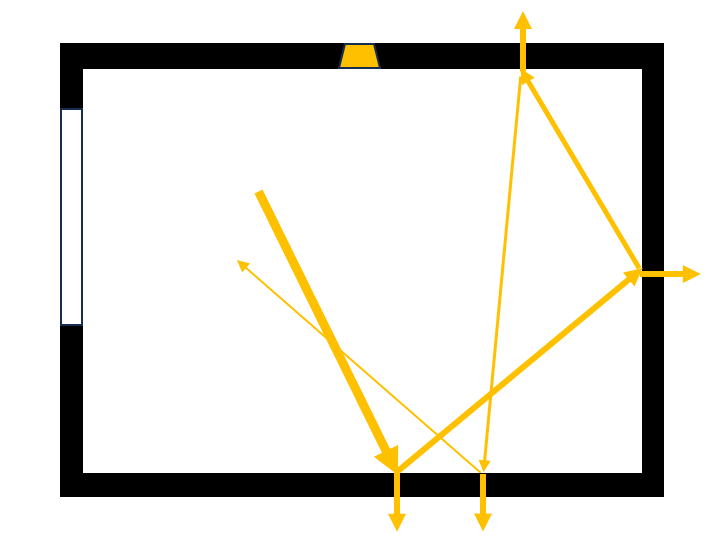
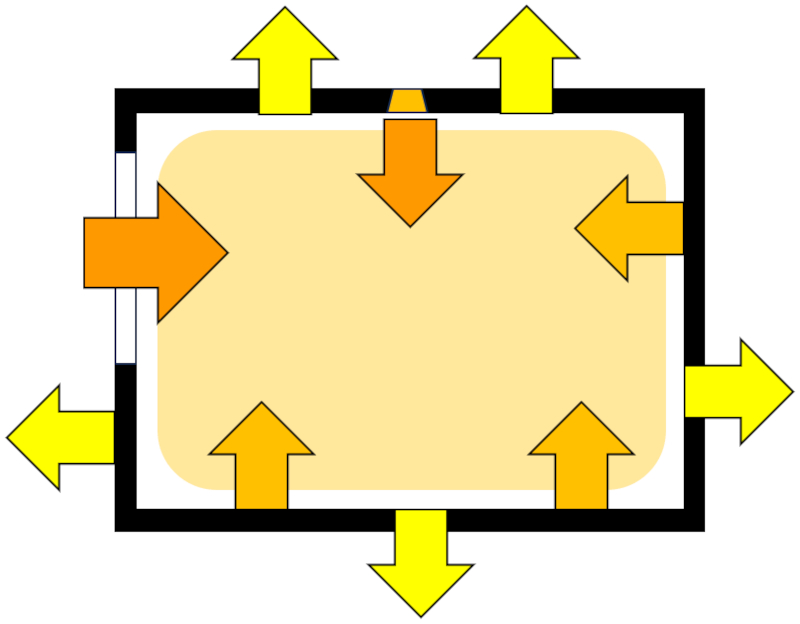
Since the walls are not perfectly smooth, the light reflects isotropically, meaning without favoring any particular direction. In the end, there is an incoming photon flux through the windows and/or lamps, and a dominant absorption flux on the walls, which, in a steady-state situation, will be equal to the incoming flux:
ID:(137, 0)
Reference photon concentration
Concept
The amount of light, represented by the number of photons entering the room per unit of time, whether through windows or lamps, can be estimated using the variables the intensity ($I$) and source surface ($S_w$), considering that each photon possesses an energy of the photon energy ($\epsilon$). This relationship is given by the formula:
$\displaystyle\frac{I S_w}{\epsilon}$
Which is illustrated in the following graph:
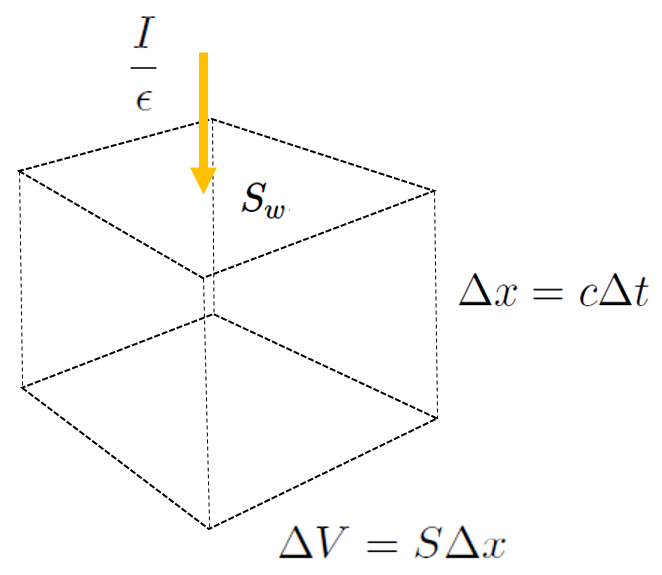
The photons that enter the space are lost due to absorption by the surfaces of the walls, ceiling, and floor, according to the value wall surfaces ($S$). The number of photons impacting these surfaces is proportional to the photon concentration ($n$), and the fraction absorbed is the complement of the albedo ($a$). Additionally, if the distribution of photons is anisotropic, only 1/6 of the photons near the surface will travel in the direction toward it. Therefore, the flux of absorbed photons can be expressed as:
$\displaystyle\frac{1}{6} n S (1-a)$
This relationship is also represented in the following graph:
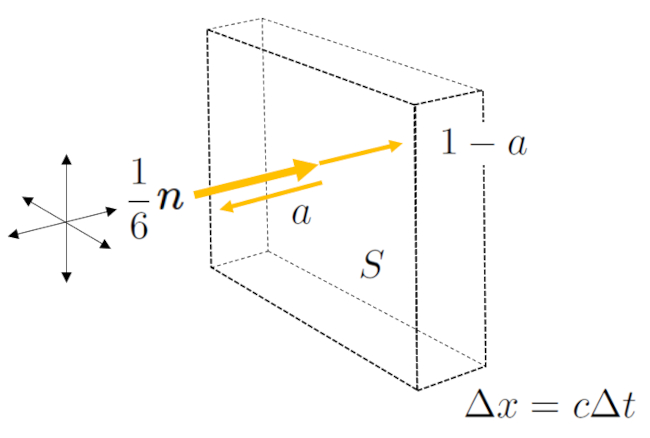
In general, the second flux is smaller than the first, implying that the incoming flux is absorbed through multiple reflections on the walls. However, this process is so fast that the human eye cannot perceive it, so the interruption of a light source results in an apparent instantaneous darkening.
ID:(139, 0)
Photon balance
Concept
Considering the photon flux entering and the one being absorbed, it is possible to calculate how the photon concentration ($n$) varies as a function of the time ($t$) in volume of space ($V$). This is represented in the following graph:
indicating that the variation of the photon concentration ($n$) with respect to the time ($t$),
$\displaystyle\frac{dn}{dt}$
will be equal to the incoming flux:
$\displaystyle\frac{S_w I}{\epsilon V}$
involving the variables source surface ($S_w$), the intensity ($I$), the photon energy ($\epsilon$), and volume of space ($V$), minus the loss due to absorption by the walls:
$\displaystyle\frac{1}{6}\displaystyle\frac{S (1-a) c n}{V}$
with the variables the speed of Light ($c$), the albedo ($a$), and wall surfaces ($S$), resulting in the following equation:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
ID:(15869, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ c = \nu \lambda $
c = nu * lambda
$ \epsilon = h \nu $
e = h * nu
$ n = n_a + (n_0 - n_a) e^{- t / \tau }$
n = n_a +( n_0 - n_a )*exp(- t / tau )
$ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$
n_a = 6 * I * S_w /( c *(1- a )* e * S )
$ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$
tau = 6* V /( c *(1 - a )* S )
$\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$
@DIF( n , t , 1) = - c * S *(1- a ) * n /(6* V ) + S_w * I /( e * V )
ID:(15874, 0)
Photon balance
Equation
The variation of the photon concentration ($n$) as a function of the time ($t$) is due to the incoming flux minus the fraction that is absorbed. Therefore, by using the variables source surface ($S_w$), the intensity ($I$), wall surfaces ($S$), the albedo ($a$), volume of space ($V$), the speed of Light ($c$), and the photon energy ($\epsilon$), the following equation is obtained:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
The variation of the photon concentration ($n$) with respect to the time ($t$),
$\displaystyle\frac{dn}{dt}$
will be equal to the incoming flux:
$\displaystyle\frac{S_w I}{\epsilon V}$
which involves the variables source surface ($S_w$), the intensity ($I$), the photon energy ($\epsilon$), and volume of space ($V$), minus the loss due to absorption by the walls:
$\displaystyle\frac{1}{6}\displaystyle\frac{S (1-a) c n}{V}$
using the variables the speed of Light ($c$), the albedo ($a$), and wall surfaces ($S$), resulting in the following equation:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
ID:(15870, 0)
Frequency and Wavelength of Photon
Equation
The photon is described as a wave, and the photon frequency ($\nu$) is related to ($$) through the speed of Light ($c$), according to the following formula:
| $ c = \nu \lambda $ |
Given that the photon frequency ($\nu$) is the inverse of the period ($T$):
$\nu=\displaystyle\frac{1}{T}$
this means that the speed of Light ($c$) is equal to the distance traveled in one oscillation, which is ($$), divided by the elapsed time, which corresponds to the period:
$c=\displaystyle\frac{\lambda}{T}$
In other words, the following relationship holds:
| $ c = \nu \lambda $ |
This formula corresponds to the mechanical relationship that states the wave speed is equal to the wavelength (distance traveled) divided by the oscillation period, or inversely proportional to the frequency (the inverse of the period).
ID:(3953, 0)
Photon energy
Equation
The color of light is associated with its the photon frequency ($\nu$), and there is a direct relationship between this frequency and the photon energy ($\epsilon$):
| $ \epsilon = h \nu $ |
where the planck constant ($h$) has a value of $6.62\times 10^{-34} , \text{Js}$.
ID:(3341, 0)
Stationary case photon concentration
Equation
In the steady-state case, the number of photons entering the room is equal to the number of photons absorbed, which means there is a the asymptotic photon concentration ($n_a$) that can be calculated using source surface ($S_w$), the intensity ($I$), wall surfaces ($S$), the albedo ($a$), the speed of Light ($c$), and the photon energy ($\epsilon$) through the following equation:
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
The photon flux in a room is described by the photon concentration ($n$) as a function of the time ($t$), using the variables source surface ($S_w$), the intensity ($I$), wall surfaces ($S$), the albedo ($a$), the speed of Light ($c$), and the photon energy ($\epsilon$), according to the following equation:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
In the steady-state case, the derivative is zero, and by solving the equation for the photon concentration ($n$), we can define the asymptotic photon concentration ($n_a$) using the following relation:
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
¨
It is important to keep in mind that this represents an average light level within a room, and it will vary depending on the location inside the room. The light intensity will change depending on whether direct light is received from the source or through multiple reflections, which progressively decrease, creating areas where only a small amount of light reaches.
ID:(15868, 0)
Absorption relaxation time
Equation
Using the photon balance equation and the steady-state photon concentration, a timescale the relaxation time ($\tau$) can be determined, which depends on volume of space ($V$), wall surfaces ($S$), the albedo ($a$), and the speed of Light ($c$), through:
| $ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$ |
Since the variation of the photon concentration ($n$) as a function of the time ($t$) is due to the incoming flux minus the fraction that is absorbed, the equation can be expressed using the variables source surface ($S_w$), the intensity ($I$), wall surfaces ($S$), the albedo ($a$), volume of space ($V$), the speed of Light ($c$), and the photon energy ($\epsilon$), resulting in the following equation:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
With the relation for the asymptotic photon concentration ($n_a$) given by:
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
the equation can be rewritten as:
$\displaystyle\frac{dn}{dt} = \displaystyle\frac{1}{\tau}(n_0-n)$
where the relaxation time ($\tau$) is:
| $ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$ |
ID:(15872, 0)
Time evolution of photon concentration
Equation
By solving the photon balance equation, it follows that the photon concentration ($n$) as a function of the time ($t$), along with the variables the initial concentration ($n_0$), the asymptotic photon concentration ($n_a$), and the relaxation time ($\tau$), is:
| $ n = n_a + (n_0 - n_a) e^{- t / \tau }$ |
Since the variation of the photon concentration ($n$) as a function of the time ($t$) is due to the incoming flux minus the absorbed fraction, the equation can be expressed using the variables source surface ($S_w$), the intensity ($I$), wall surfaces ($S$), the albedo ($a$), volume of space ($V$), the speed of Light ($c$), and the photon energy ($\epsilon$), leading to the following relationship:
| $\displaystyle\frac{ dn }{ dt } = -\displaystyle\frac{1}{6} c \displaystyle\frac{ S }{ V }(1-a) n + \displaystyle\frac{ S_w I }{ \epsilon V }$ |
With the relation for the asymptotic photon concentration ($n_a$) given by:
| $ n_a = \displaystyle\frac{6 I }{ c (1- a )\epsilon}\displaystyle\frac{ S_w }{ S }$ |
and with the relaxation time ($\tau$):
| $ \tau = \displaystyle\frac{ 6 V }{ c (1- a ) S }$ |
the equation can be rewritten as:
$\displaystyle\frac{dn}{dt} = \displaystyle\frac{1}{\tau}(n_0-n)$
whose solution is:
| $ n = n_a + (n_0 - n_a) e^{- t / \tau }$ |
with the initial concentration ($n_0$).
ID:(15871, 0)