Usuario:


Campton Scattering
Storyboard

>Modelo

ID:(1074, 0)


Scattering de Compton
Definición

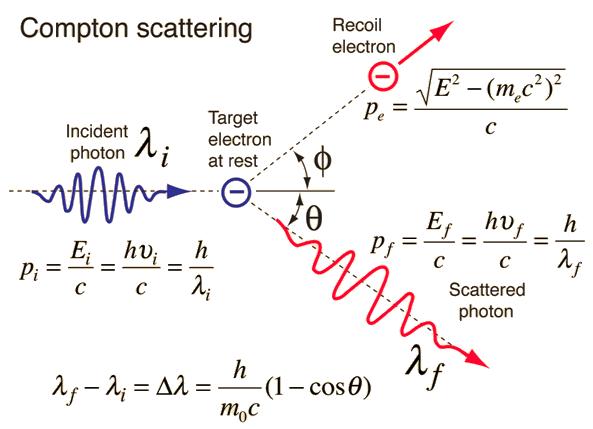
El scattering de Compton ocurre entre un fotón y un electron de un atomo y lleva a la ionización de esta último:

ID:(8727, 0)


Proceso de multiples Scattering
Imagen

Como el fotón pierde energía en el scattering de Compton es capaz de ionizar atomos con electrones superiores existiendo multiples scatterings:

ID:(8728, 0)


Experimento de Compton
Nota

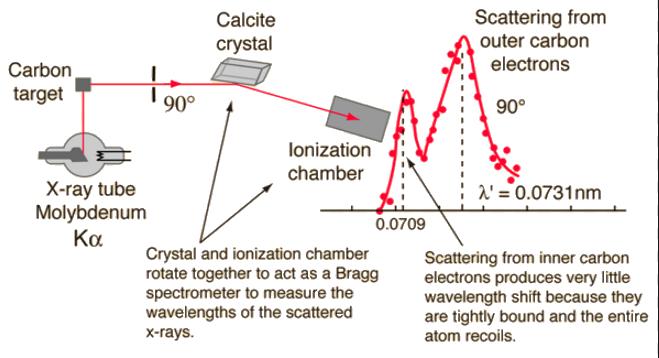
El fotón se genera con un tubo de rayos X, incide sobre el target a estudiar y los fotones que realizaron scattering. El haz de fotones que se originan por el scattering son reflectados sobre un cristal para así descomponer el haz según el largo de onda de los fotones. Finalmente se mide la intensidad del haz resultante con una cámara de ionización:

ID:(8729, 0)


Energía adquirida por el Electrón
Cita

Como el largo de onda del fotón resultante del scattering es $\lambda'$ dado por

$\lambda'-\lambda=\lambda_c(1-\cos\theta)$



y la energía se puede calcular mediante

$E=\displaystyle\frac{hc}{\lambda}$

se puede ver que la energía por la energía en reposo del electron ganada por este es

$\Delta\epsilon_e=\epsilon\left(1-\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}\right)$



con

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

ID:(8736, 0)


Sección Eficaz de Compton
Ejercicio

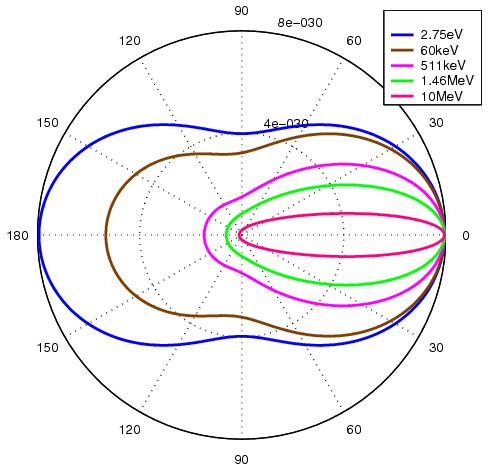
La sección eficaz del scattering de Compton según el modelo de Klein-Nishina se deja representar en función del angulo de scattering como se ve a continuación:

ID:(8723, 0)


Sección eficaz total en función de la Energía
Ecuación

A medida que la energía del fotón decrece aumenta la sección eficaz total hasta que decrece abruptamente y ya no ocurren scattering de Compton:

ID:(8733, 0)


Codigo
Script

Si un foton sufre scattering de Compton, su largo de onda original \lambda pasara a tener un valor de \lambda'segun el angulo \theta en que se desvía, según:

\lambda' -\lambda=\displaystyle\frac{h}{m_ec}(1-\cos\theta)

Si se despeja \cos\theta se obtiene

\cos\theta=1+\displaystyle\frac{m_ec}{h}(\lambda -\lambda')

Como la energía del foton es

E=h

u=\displaystyle\frac{hc}{\lambda}

se puede expresar el largo de onda como

\lambda=\displaystyle\frac{hc}{E}

Si se discretiza la energía en intervalos \Delta E se tiene que

E=n\Delta E

Como el coseno del ángulo es

\cos\theta=1+\displaystyle\frac{m_ec}{h}(\displaystyle\frac{hc}{E} -\displaystyle\frac{hc}{E'})

en la aproximación discreta se tendrá

\cos\theta=1+\displaystyle\frac{m_ec^2}{\Delta E}(\displaystyle\frac{1}{n} -\displaystyle\frac{1}{n'})

Si se introduce la variable

f\equiv \displaystyle\frac{m_ec^2}{\Delta E}

y un contador que tiene valores entre 0 y Ne. Como los indice n y n' comienzan en cero y el primer intervalo tiene una energía \Delta E se tiene que a los indices a usar se le debe sumar uno.

De esta forma se obtiene que el coseno es

```

cs = 1+f*(1/(in_e+1)-1/(out_e+1));

```

Con la sección eficaz de Klein-Nishina

\displaystyle\frac{d\sigma}{d\Omega}=\displaystyle\frac{1}{2}\alpha^2r_c^2P^2\left[P+\displaystyle\frac{1}{P}-\sin^2\theta\right]

el angulo solido

d\Omega=\sin\theta d\theta d\phi

y el factor P

P=\displaystyle\frac{\lambda}{\lambda'}=\displaystyle\frac{E'}{E}=\displaystyle\frac{n'}{n}

que se puede calcular como

```

P=(out_e+1)/(in_e+1)

```

se tiene que la suma de la sección eficaz sobre \theta (sin la constante ya que se normaliza al final)

```

dataKNSec[in_e][out_e] = Math.pow(P,2)*(P+1/P-Math.pow(se,2))*se;

```

Finalmente se puede normalizar esta expresión y multiplicar con el factor

\displaystyle\frac{1}{2}\alpha^2r_c^2\pi=\pi\alpha^2r_c^2

ID:(9775, 0)


Campton Scattering
Descripción

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

Ejemplos

El scattering de Compton ocurre entre un fot n y un electron de un atomo y lleva a la ionizaci n de esta ltimo:

(ID 8727)

Al sufrir un fot n de largo de onda $\lambda$ un scattering de Compton tiene un largo de onda $$\lambda'$ dado por

$\lambda'-\lambda=\lambda_c(1-\cos\theta)$

si el angulo de scattering es $\theta$ y $\lambda_c$ es el largo de onda de Compton que es del orden de 2.43E-12 m.

(ID 8734)

Como el fot n pierde energ a en el scattering de Compton es capaz de ionizar atomos con electrones superiores existiendo multiples scatterings:

(ID 8728)

El fot n se genera con un tubo de rayos X, incide sobre el target a estudiar y los fotones que realizaron scattering. El haz de fotones que se originan por el scattering son reflectados sobre un cristal para as descomponer el haz seg n el largo de onda de los fotones. Finalmente se mide la intensidad del haz resultante con una c mara de ionizaci n:

(ID 8729)

El largo de onda reducido de Compton se define como

$\lambda_c=\displaystyle\frac{h}{m_ec}$

El largo de onda de Compton es del orden de 2.43E-12 m.

(ID 8724)

Como el largo de onda del fot n resultante del scattering es $\lambda'$ dado por

$\lambda'-\lambda=\lambda_c(1-\cos\theta)$



y la energ a se puede calcular mediante

$E=\displaystyle\frac{hc}{\lambda}$

se puede ver que la energ a por la energ a en reposo del electron ganada por este es

$\Delta\epsilon_e=\epsilon\left(1-\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}\right)$



con

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

(ID 8736)

Para simplificar las ecuaciones se puede introducir la relaci n entre la energ a $E$ y la energ a del electr n en reposo $m_ec^2$:

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

(ID 8710)

La secci n eficaz del scattering de Comption para una energ a del fot n $E$ y angulo de scattering $\theta$ es seg n Klein Nishina:

$\displaystyle\frac{d\sigma}{d\Omega}=\displaystyle\frac{1}{2}r_e^2P(\epsilon,\theta)^2[P(\epsilon,\theta)+P(\epsilon,\theta)^{-1}-1+\cos^2\theta]$



donde $r_e$ es el radio cl sico del electr n (2.8179 fm), $\epsilon$ es la proporci n de energ a del fot n con respecto a la energ a del electr n en reposo:

$\epsilon=\displaystyle\frac{E}{m_ec^2}$



y

$P(\epsilon,\theta)=\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}$

es la proporci n de energ a del fot n despu s y antes del scattering.

(ID 8709)

La proporci n de la energ a del fot n despu s y antes del scattering de Compton es

$P(\epsilon,\theta)=\displaystyle\frac{1}{1+\epsilon(1-\cos\theta)}$



donde $\epsilon$ es la energ a inicial del fot n dividida por la masa en reposo del electr n

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

(ID 8725)

La secci n eficaz del scattering de Compton seg n el modelo de Klein-Nishina se deja representar en funci n del angulo de scattering como se ve a continuaci n:

(ID 8723)

La secci n eficaz total del scattering de Comption se puede calcular de la secci n eficaz es seg n Klein Nishina:

$\displaystyle\frac{d\sigma}{d\Omega}=\displaystyle\frac{1}{2}r_e^2P(\epsilon,\theta)^2[P(\epsilon,\theta)+P(\epsilon,\theta)^{-1}-1+\cos^2\theta]$



integrando en el angulo solido obteni ndose

$\sigma=2\pi r_0^2\left(\displaystyle\frac{1+\epsilon}{\epsilon}\left[\displaystyle\frac{2(1+\epsilon)}{1+2\epsilon}-\displaystyle\frac{1}{\epsilon}\ln(1+2\epsilon)\right]+\displaystyle\frac{1}{2\epsilon}\ln(1+2\epsilon)-\displaystyle\frac{1+3\epsilon}{(1+2\epsilon)^2}\right)$



con

$\epsilon=\displaystyle\frac{E}{m_ec^2}$

el factor de energ a y $r_e$ el radio clasico del electr n (2.817E-15 m).

(ID 8726)

A medida que la energ a del fot n decrece aumenta la secci n eficaz total hasta que decrece abruptamente y ya no ocurren scattering de Compton:

(ID 8733)

Si un foton sufre scattering de Compton, su largo de onda original \lambda pasara a tener un valor de \lambda'segun el angulo \theta en que se desv a, seg n:

\lambda' -\lambda=\displaystyle\frac{h}{m_ec}(1-\cos\theta)

Si se despeja \cos\theta se obtiene

\cos\theta=1+\displaystyle\frac{m_ec}{h}(\lambda -\lambda')

Como la energ a del foton es

E=h

u=\displaystyle\frac{hc}{\lambda}

se puede expresar el largo de onda como

\lambda=\displaystyle\frac{hc}{E}

Si se discretiza la energ a en intervalos \Delta E se tiene que

E=n\Delta E

Como el coseno del ngulo es

\cos\theta=1+\displaystyle\frac{m_ec}{h}(\displaystyle\frac{hc}{E} -\displaystyle\frac{hc}{E'})

en la aproximaci n discreta se tendr

\cos\theta=1+\displaystyle\frac{m_ec^2}{\Delta E}(\displaystyle\frac{1}{n} -\displaystyle\frac{1}{n'})

Si se introduce la variable

f\equiv \displaystyle\frac{m_ec^2}{\Delta E}

y un contador que tiene valores entre 0 y Ne. Como los indice n y n' comienzan en cero y el primer intervalo tiene una energ a \Delta E se tiene que a los indices a usar se le debe sumar uno.

De esta forma se obtiene que el coseno es

```

cs = 1+f*(1/(in_e+1)-1/(out_e+1));

```

Con la secci n eficaz de Klein-Nishina

\displaystyle\frac{d\sigma}{d\Omega}=\displaystyle\frac{1}{2}\alpha^2r_c^2P^2\left[P+\displaystyle\frac{1}{P}-\sin^2\theta\right]

el angulo solido

d\Omega=\sin\theta d\theta d\phi

y el factor P

P=\displaystyle\frac{\lambda}{\lambda'}=\displaystyle\frac{E'}{E}=\displaystyle\frac{n'}{n}

que se puede calcular como

```

P=(out_e+1)/(in_e+1)

```

se tiene que la suma de la secci n eficaz sobre \theta (sin la constante ya que se normaliza al final)

```

dataKNSec[in_e][out_e] = Math.pow(P,2)*(P+1/P-Math.pow(se,2))*se;

```

Finalmente se puede normalizar esta expresi n y multiplicar con el factor

\displaystyle\frac{1}{2}\alpha^2r_c^2\pi=\pi\alpha^2r_c^2

(ID 9775)

ID:(1074, 0)