Utilizador:
Experimento para estimar o zero absoluto
Imagem 
Se o volume de um gás for medido a 0°C e 100°C, observa-se um comportamento linear no gráfico de volume-temperatura. Se a reta for projetada, pode-se ver que em algum ponto das temperaturas negativas (na escala Celsius ou Fahrenheit), o volume atingirá o valor zero. Esse ponto é chamado de zero absoluto.
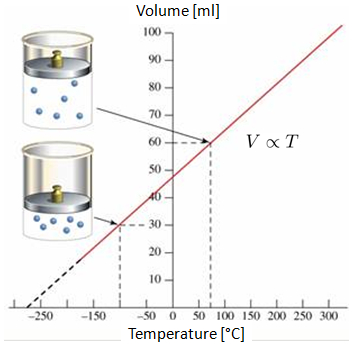
É importante ressaltar que na realidade não se alcança a situação em que o volume chega a zero, pois todos os gases condensam e solidificam muito antes de atingir o zero absoluto.
ID:(11169, 0)
Prático: Temperatura absoluta
Nota
No seguinte vídeo, é mostrado como os volumes de um gás em diferentes temperaturas são determinados no laboratório, a fim de traçar a curva de volume-temperatura em pressão constante. Através da interseção da reta com o eixo da temperatura, é possível determinar a temperatura absoluta na qual teoricamente o volume deveria ser zero:
Os valores obtidos são:
| V [ml] | T [C] |
| 152.1 | 3.7 |
| 165.1 | 21.9 |
| 183.1 | 43.0 |
Esses valores são representados graficamente, incluindo a reta calculada por regressão:
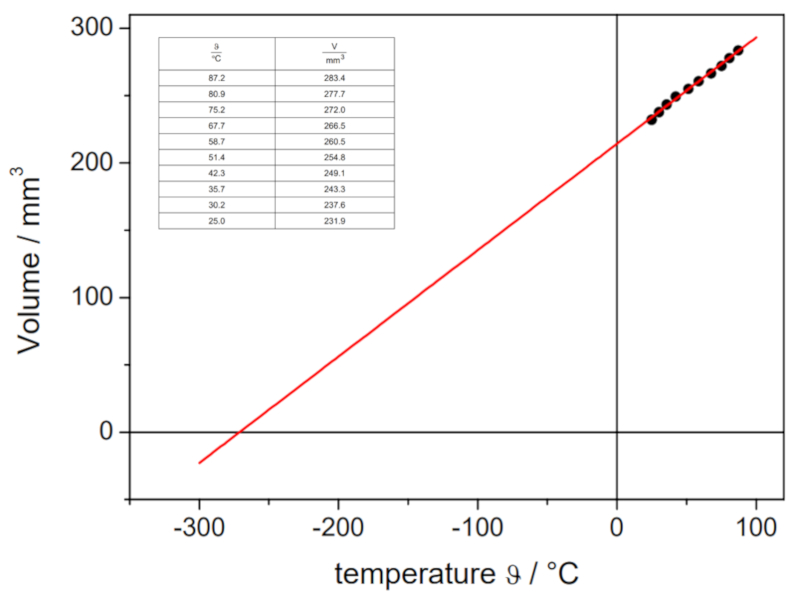
Essa estimativa nos dá um valor de -148 °C, que difere do valor real de -273.15 °C.
ID:(11173, 0)
Temperatura absoluta prática
Descrição
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
A lei de Charles estabelece que, com la pressão ($p$) constante, a propor o de o volume ($V$) com la temperatura absoluta ($T$) igual a la constante da lei de Charles ($C_c$):
| $\displaystyle\frac{ V }{ T } = C_c$ |
Isso significa que se um g s passa de um estado inicial (o volume no estado i ($V_i$) e la temperatura no estado inicial ($T_i$)) para um estado final (o volume no estado f ($V_f$) e la temperatura no estado final ($T_f$)), mantendo la pressão ($p$) constante, ele deve sempre obedecer lei de Charles:
$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$
Portanto, temos:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
(ID 3492)
Exemplos
(ID 15261)
Se o volume de um g s for medido a 0 C e 100 C, observa-se um comportamento linear no gr fico de volume-temperatura. Se a reta for projetada, pode-se ver que em algum ponto das temperaturas negativas (na escala Celsius ou Fahrenheit), o volume atingir o valor zero. Esse ponto chamado de zero absoluto.
importante ressaltar que na realidade n o se alcan a a situa o em que o volume chega a zero, pois todos os gases condensam e solidificam muito antes de atingir o zero absoluto.
(ID 11169)
No seguinte v deo, mostrado como os volumes de um g s em diferentes temperaturas s o determinados no laborat rio, a fim de tra ar a curva de volume-temperatura em press o constante. Atrav s da interse o da reta com o eixo da temperatura, poss vel determinar a temperatura absoluta na qual teoricamente o volume deveria ser zero:
Os valores obtidos s o:
| V [ml] | T [C] |
| 152.1 | 3.7 |
| 165.1 | 21.9 |
| 183.1 | 43.0 |
Esses valores s o representados graficamente, incluindo a reta calculada por regress o:
Essa estimativa nos d um valor de -148 C, que difere do valor real de -273.15 C.
(ID 11173)
(ID 15320)
A lei de Charles estabelece uma rela o entre o volume ($V$) e la temperatura absoluta ($T$), indicando que sua propor o igual a la constante da lei de Charles ($C_c$), da seguinte forma:
| $\displaystyle\frac{ V }{ T } = C_c$ |
(ID 583)
A lei de Charles estabelece uma rela o entre o volume ($V$) e la temperatura absoluta ($T$), indicando que sua propor o igual a la constante da lei de Charles ($C_c$), da seguinte forma:
| $\displaystyle\frac{ V }{ T } = C_c$ |
(ID 583)
Se um g s passa de um estado inicial (i) para um estado final (f) com la pressão ($p$) constante, ent o para o volume no estado i ($V_i$), o volume no estado f ($V_f$), la temperatura no estado inicial ($T_i$) e la temperatura no estado final ($T_f$) v lido:
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
(ID 3492)
ID:(1478, 0)