Utilisateur:
Expérience pour estimer le zéro absolu
Description 
Si le volume d'un gaz est mesuré à 0°C et 100°C, on observe un comportement linéaire sur le graphique volume-température. Si la droite est prolongée, on peut constater qu\'à un certain point des températures négatives (en échelle Celsius ou Fahrenheit), le volume atteindra zéro. Ce point est appelé zéro absolu.
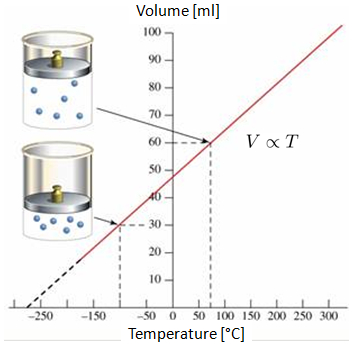
Il est important de noter que dans la réalité, la situation où le volume atteint zéro n\'est pas atteignable, car tous les gaz se condensent et se solidifient bien avant d\'atteindre le zéro absolu.
ID:(11169, 0)
Pratique : Température absolue
Description
Dans la vidéo suivante, on montre comment les volumes d'un gaz à différentes températures sont déterminés en laboratoire afin de tracer la courbe volume-température à pression constante. L'intersection de la droite avec l\'axe des températures permet de déterminer la température absolue théorique à laquelle le volume devrait être nul :
Les valeurs obtenues sont les suivantes :
| V [ml] | T [C] |
| 152.1 | 3.7 |
| 165.1 | 21.9 |
| 183.1 | 43.0 |
Ces valeurs sont représentées graphiquement, y compris la droite calculée par régression :
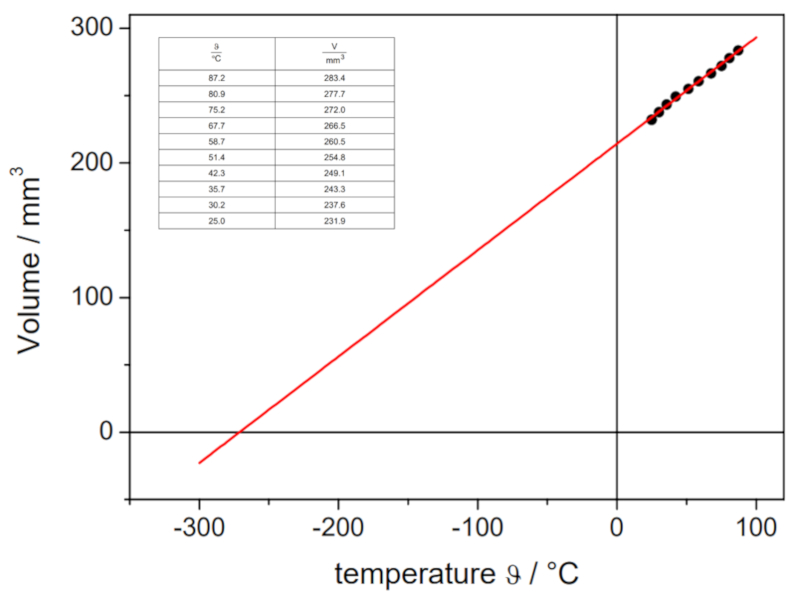
Cette estimation donne une valeur de -148 °C, qui diffère de la valeur réelle de -273,15 °C.
ID:(11173, 0)
Température absolue pratique
Modèle
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
La loi de Charles tablit que, avec a pression ($p$) constant, le rapport de le volume ($V$) A température absolue ($T$) est gal a constante de la loi de Charles ($C_c$) :
| $\displaystyle\frac{ V }{ T } = C_c$ |
Cela signifie que si un gaz passe d'un tat initial (le volume à l'état i ($V_i$) et a température à l'état initial ($T_i$)) un tat final (le volume à l'état f ($V_f$) et a température à l'état final ($T_f$)), en maintenant a pression ($p$) constant, il doit toujours ob ir la loi de Charles :
$\displaystyle\frac{V_i}{T_i} = C_c = \displaystyle\frac{V_f}{T_f}$
Ainsi, nous avons :
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
(ID 3492)
Exemples
(ID 15261)
Si le volume d'un gaz est mesur 0 C et 100 C, on observe un comportement lin aire sur le graphique volume-temp rature. Si la droite est prolong e, on peut constater qu\' un certain point des temp ratures n gatives (en chelle Celsius ou Fahrenheit), le volume atteindra z ro. Ce point est appel z ro absolu.
Il est important de noter que dans la r alit , la situation o le volume atteint z ro n\'est pas atteignable, car tous les gaz se condensent et se solidifient bien avant d\'atteindre le z ro absolu.
(ID 11169)
Dans la vid o suivante, on montre comment les volumes d'un gaz diff rentes temp ratures sont d termin s en laboratoire afin de tracer la courbe volume-temp rature pression constante. L'intersection de la droite avec l\'axe des temp ratures permet de d terminer la temp rature absolue th orique laquelle le volume devrait tre nul :
Les valeurs obtenues sont les suivantes :
| V [ml] | T [C] |
| 152.1 | 3.7 |
| 165.1 | 21.9 |
| 183.1 | 43.0 |
Ces valeurs sont repr sent es graphiquement, y compris la droite calcul e par r gression :
Cette estimation donne une valeur de -148 C, qui diff re de la valeur r elle de -273,15 C.
(ID 11173)
(ID 15320)
ID:(1478, 0)