Druyd:Knowledge

Poisson distributions

Storyboard

In the case where the probability is very small, the binomial distribution is reduced to a Poisson distribution.

>Model

ID:(1555, 0)

Example comparison with Poisson distribution

Definition

ID:(7794, 0)

Poisson distributions

Description

In the case where the probability is very small, the binomial distribution is reduced to a Poisson distribution.

Variables

Symbol

Text

Variable

Value

Units

Calculate

MKS Value

MKS Units

$e^{-\lambda}$

elam

Exponential $e^{-\lambda}$

$N^n$

N^n

Exponential $N^n$

$n!$

Factorial $n!$

$n$

Number

$N$

Número total de pasos

$n$

Número totales de pasos a la izquierda

$\lambda^n$

lambda_n

Power of lambda $\lambda^n$

$P_N(m)$

P_Nm

Probabilidad de $n_1$ de $N$ pasos hacia la izquierda

$p$

Probabilidad de pasos hacia la izquierda

$\lambda$

lam

Standard Deviation Poisson

Calculations

Equation

Number

First, select the equation:

, then, select the variable:

Symbol

Equation

Solved

Translated

Calculations

Symbol

Equation

Solved

Translated

Variable

Given

Calculate

Target :

Equation

To be used

Equations

$ P_{\lambda}(n) =\displaystyle\frac{ \lambda ^ n }{ n! }e^{- \lambda }$

P_lambda(n) =( lambda ^ n / n! )*exp(- lambda )

(ID 3369)

$N^n\sim\displaystyle\frac{N!}{(N-n)!}$

N^n\sim\displaystyle\frac{N!}{(N-n)!}

(ID 4738)

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

W_N(n) =math.factorial( N )* p ^ n *(1- p )^( N - n )/(math.factorial( n )*math.factorial( N - n ))

(ID 8961)

$\lambda=Np$

lambda=Np

(ID 8964)

$e^{-\lambda}\sim (1-p)^{N-n}$

e^{-\lambda}\sim (1-p)^{N-n}

(ID 8968)

$\displaystyle\frac{N!}{(N-n)!}p^n\sim \lambda^n$

\displaystyle\frac{N!}{(N-n)!}p^n\sim \lambda^n

(ID 8969)

Examples

Example comparison with Poisson distribution

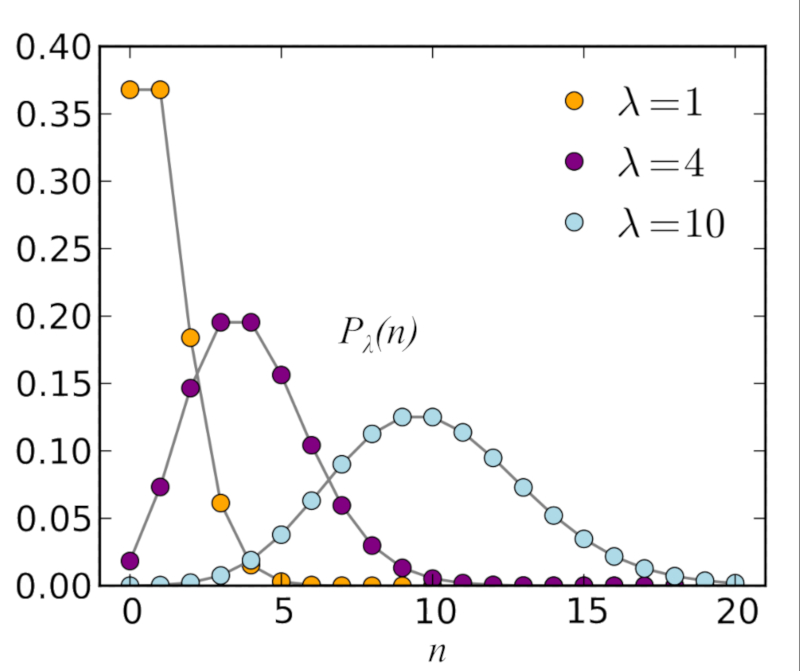
If we study the binomial distribution for large numbers N and very small probability p \ ll 1 it can be approximated using a Poisson distribution. The comparison can be done with the following simulator:

(ID 7794)

ID:(1555, 0)