User:


Gaussian distribution
Storyboard

In the limit of similar probabilities the binomial distribution is reduced in the continuous limit to the Gaussean distribution.

>Model

ID:(1556, 0)


Example comparison with Gaussian distribution
Definition

If we study the binomial distribution for large numbers N and probabilities around 1/2

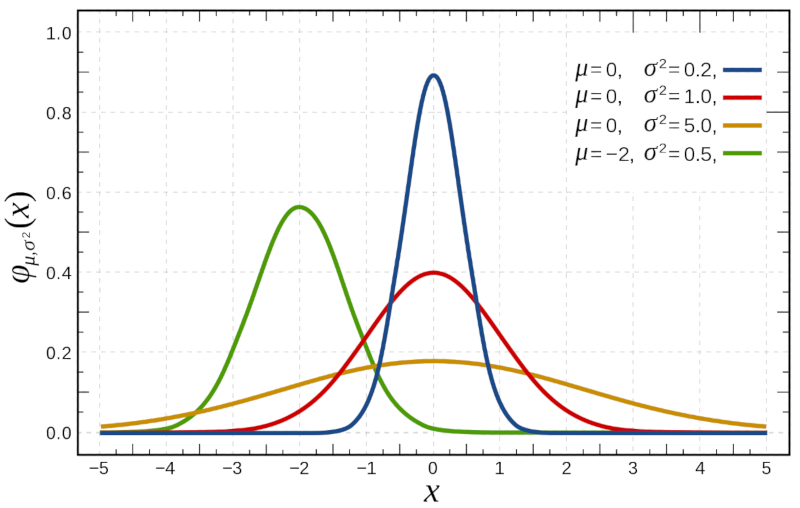
$P(x)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}$



which is represented below:

ID:(7793, 0)


Gaussian distribution
Description

In the limit of similar probabilities the binomial distribution is reduced in the continuous limit to the Gaussean distribution.

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$\sigma$
sigma
Desviación estándar de Gauss
-
$n$
n
Number
-
$q$
q
Número de pasos hacia la derecha
-
$n_1$
n_1
Número de pasos hacia la izquierda
-
$N$
N
Número total de pasos
-
$n$
n
Número totales de pasos a la izquierda
-
$u$
u
Parameter $u$
-
$s$
s
Posición camino aleatorio
m
$\mu$
mu
Posición media
m
$P_N(m)$
P_Nm
Probabilidad de $n_1$ de $N$ pasos hacia la izquierda
-
$p$
p
Probabilidad de pasos hacia la izquierda
-
$a$
a
Step size
m

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

Examples

Con la probabilidad de que se de un numero definido de pasos a la derecha e izquierda esta dada por

$W_N(n_1,n_2)=\displaystyle\frac{N!}{n_1!n_2!}p^{n_1}q^{n_2}$



con el n mero total de pasos es

$N=n_1+n_2$



y solo existe la probabilidad de ir a la derecha o a la izquierda, con se tiene para las probabilidades que

$p+q=1$



por lo que con se tiene la distribuci n binomial

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

(ID 8961)

With the Stirling approximation

equation=8966

and the change of variables

equation=8996

you get that

equation

(ID 8998)

With the Stirling approximation

equation=8966

and the change of variables

equation=11431

you get that

equation

(ID 9003)

With the Stirling approximation

equation=8966

and the change of variables

equation=8997

the expression is

equation

(ID 8999)

In the case of medium probabilities (p \sim q \sim 1/2) and large numbers N it can be shown with

$N!\sim\sqrt{2\pi N}\left(\displaystyle\frac{N}{e}\right)^N$



$n!\sim\sqrt{2\pi n}\left(\displaystyle\frac{n}{e}\right)^n$



and

$(N-n)!\sim\sqrt{2\pi(N-n)}\left(\displaystyle\frac{N-n}{e}\right)^{N-n}$



is obtained

$\displaystyle\frac{N!}{n!(N-n)!}\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}$

(ID 507)

The expression

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$



is reduced by

$\displaystyle\frac{N!}{n!(N-n)!}\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}$



to representation

$W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}p^n(1-p)^{N-n}$

(ID 506)

If total N steps are taken with a probability p in the right direction and these have a length a the expected final position will be

$\mu=aNp$

(ID 9008)

To obtain the Gaussian distribution it is necessary to develop the distribution around its deviation from its mean position that can be given by

$x=(n-Np)a$

(ID 8973)

As the way is

$x=(n-Np)a$



factor n/N can be written as

$\displaystyle\frac{n}{N}=p\left(1+\displaystyle\frac{x}{aNp}\right)$

(ID 9004)

As the way is

$x=(n-Np)a$



factor n/N can be written as

$\displaystyle\frac{N-n}{N}=(1-p)\left(1-\displaystyle\frac{x}{aN(1-p)}\right)$

(ID 9005)

If large numbers and probabilities around 1/2 are entered in the binomial distribution for the case

$W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}p^n(1-p)^{N-n}$



the expressions

$\displaystyle\frac{n}{N}=p\left(1+\displaystyle\frac{x}{aNp}\right)$



and

$\displaystyle\frac{N-n}{N}=(1-p)\left(1-\displaystyle\frac{x}{aN(1-p)}\right)$




a distribution of the form is obtained

$W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}p(1-p)}\left(1+\displaystyle\frac{x}{aNp}\right)^{-n-1/2}\left(1-\displaystyle\frac{x}{aN(1-p)}\right)^{-N+n-1/2}$

(ID 8974)

To develop the 1+x/aNp factor you can work with the variable change

$u=\displaystyle\frac{x}{aNp}$

(ID 9021)

With the approximation

$1+u\sim e^{u-\frac{1}{2}u^2}$



it has to

$\left(1+\displaystyle\frac{x}{aNp}\right)\sim e^{x/aNp-x^2/2a^2N^2p^2}$

(ID 9006)

To develop the factor 1+x/aN(1-p) you can work with the variable change

$u=\displaystyle\frac{x}{aN(1-p)}$

(ID 9022)

With the approximation

$1+u\sim e^{u-\frac{1}{2}u^2}$



it has to

$\left(1-\displaystyle\frac{x}{aN(1-p)}\right)\sim e^{-x/aN(1-p)-x^2/2a^2N^2(1-p)^2}$

(ID 9007)

It can be shown that for a large number N and probability p neither too small nor too close to 1, the binomial distribution is reduced to a gausseana for the position x=na:

$P(x)=\displaystyle\frac{1}{\sqrt{2\pi N^2p(1-p)}}e^{-(x-aNp)^2/2N^2p(1-p)}$

In this case, the probability q was replaced by 1-p.

(ID 3367)

$\begin{matrix}

P(x) & = & \displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}\\

\sigma^2 & = & Np(1-p)\\

\end{matrix}

$

(ID 3368)

The standard deviation of the binomial distribution at the limit N large and p medium is

$ \sigma^2 = N ^2 p (1- p )$

(ID 8963)

If we study the binomial distribution for large numbers N and probabilities around 1/2

$P(x)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}$



which is represented below:

(ID 7793)

ID:(1556, 0)