User: 
Flat Mirror
Storyboard 
In the case of a flat mirror, the light is reflected at an angle identical to the one it affected.
In general, the light does not have the information that has been reflected with what the eye assumes that the light originates 'behind' the mirror.
ID:(1263, 0)
La ley de reflexión
Image
Aplicando el principio de Huygens se muestra que un haz que incide sobre una superficie se refleja bajo un angulo igual al de incidencia:
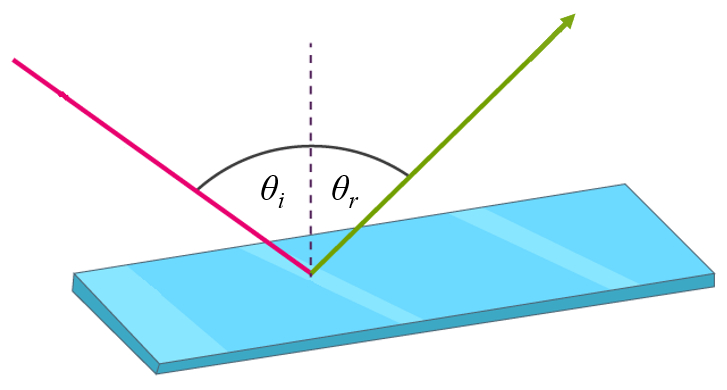
ID:(12758, 0)
Relación entre ángulos de incidencia y reflexión
Image
Del análisis mediante el principio de Huygens se concluye que los ángulos de incidencia y reflexión son iguales:
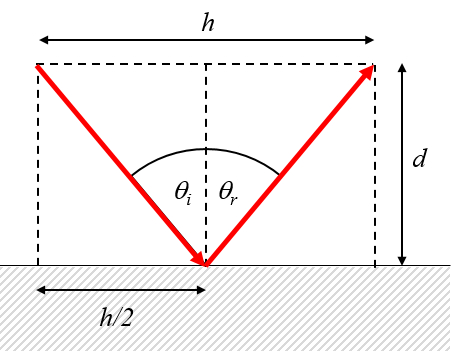
ID:(12665, 0)
Relación entre ángulos de incidencia y reflexión
Image
En caso de dos espejos con una esquina
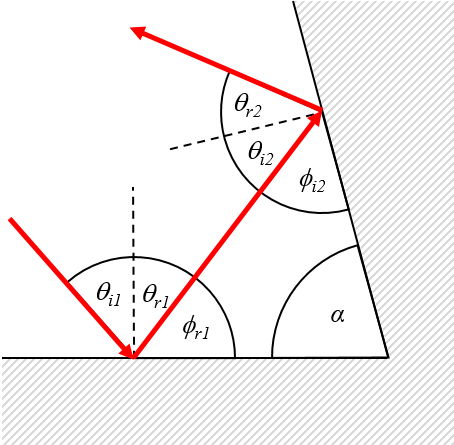
se pueden calcular los ángulos con la relación de reflexión
| \theta_i = \theta_r |
el calculo del complemento del angulo incidente
| \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r |
el calculo del complemento del angulo de reflección
| \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i |
y la relación entre los ángulos de un triangulo
| \pi = \alpha + \beta + \gamma |
ID:(12666, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
\pi = \alpha + \beta + \gamma
pi = alpha + beta + gamma
\tan \theta_i =\displaystyle\frac{ h }{2 d }
theta_i = tan( h /(2* d ))
\theta_i = \theta_r
theta_i = theta_r
\theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i
theta_ic = pi /2- theta_i
\theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r
theta_rc = pi /2- theta_r
ID:(16061, 0)
Direction of the reflected Light
Equation
Para la luz reflejada el angulo del haz respecto de la normal
| \theta_i = \theta_r |
ID:(3262, 0)
Complementary angle of incidence angle
Equation
Para el calculo de los ángulos en el caso de que los haces se reflejan en un espejo es útil poder calcular el angulo complementario al de incidencia. Por ello se tiene que
| \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i |
Como la suma de los ángulos internos en un triangulo es
| \pi = \alpha + \beta + \gamma |
se tiene que en un rectángulo, en el que uno de los ángulos es
| \theta_{ic} =\displaystyle\frac{ \pi }{2} - \theta_i |
ID:(10928, 0)
Angulo complementario del angulo de reflexión
Equation
Para el calculo de los ángulos en el caso de que los haces se reflejan en un espejo es útil poder calcular el angulo complementario al de reflexión. Por ello se tiene que
| \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r |
Como la suma de los ángulos internos en un triangulo es
| \pi = \alpha + \beta + \gamma |
se tiene que en un rectángulo, en el que uno de los ángulos es
| \theta_{rc} =\displaystyle\frac{ \pi }{2} - \theta_r |
ID:(10925, 0)
Sum of angle of a triangle
Equation
| \pi = \alpha + \beta + \gamma |
ID:(10926, 0)
Angulo de incidencia
Equation
El angulo de incidencia
| \tan \theta_i =\displaystyle\frac{ h }{2 d } |
ID:(9779, 0)
0
Video
Video: Espejo Plano