Usuario:
Espejo Cónvexo
Storyboard 
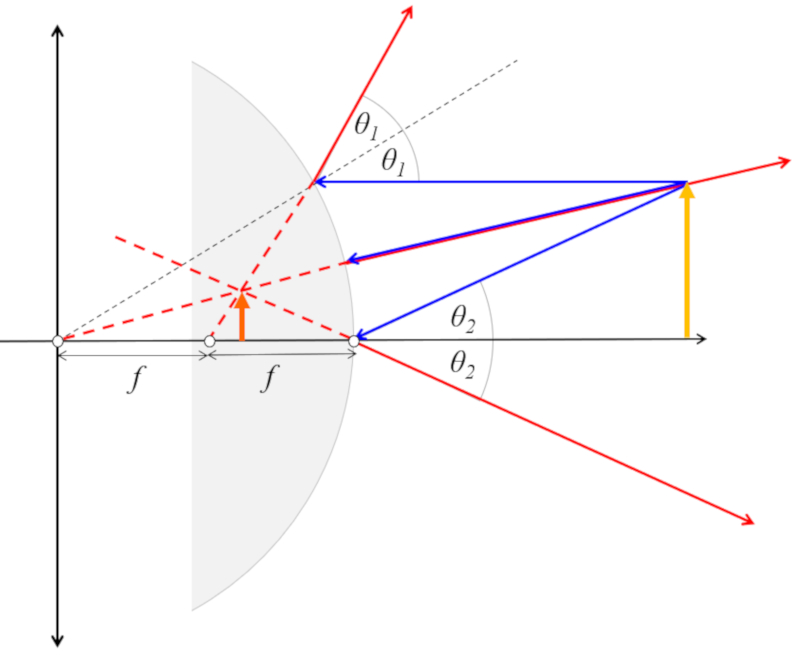
En el caso de un espejo convexo el angulo de incidencia y reflexión se determinan en función de una linea que va desde el punto de impacto y un punto que esta a dos distancias foco del lente detrás del espejo.
Un caso especial es un haz que viene paralelo al eje óptico que es reflejado como si viniera de un punto focal detrás del espejo. Viceversa si va en dirección del foco que esta detrás del espejo es reflejado en forma paralela al eje óptico. Esto ultimo se emplea en los espejo gran angular para ver 'alrededor de las esquinas'.
ID:(1265, 0)
Calculo de imagen para espejos convexo
Imagen
Para poder calcular el tamaño y el lugar en que se presentara la imagen se puede dibujar el eje óptico, el espejo convexo y un objeto en una posición y de un tamaño. Sobre este esquema se pueden dibujar tres haces:
• Un haz paralelo al eje óptico que se refleja de modo de que el angulo de incidencia y el de reflexión son iguales. El angulo de incidencia se determina entre la dirección del haz y una linea del punto de incidencia y el doble del foco (2f). Por ello el haz que se refleja pasa por el foco del espejo.
• Un haz que va en dirección del centro de curvatura del espejo se refleja en la misma dirección por el hecho que esta dirección es normal a la superficie.
• Un haz que pasa por un punto a una distancia igual al doble del foco se refleja por el mismo punto de incidencia volviendo a la fuente. Esto porque un haz por este punto incide perpendicular sobre la superficie por lo que se refleja en la misma dirección.
Si se dibuja correctamente los tres haces se cruzaran en un punto. Dicho punto corresponde a la imagen que se crea ya que todos los haces emanan de esta. Del punto se tiene la posición, el tamaño de la imagen y si esta invertida o no.
Paso del vacío, donde la velocidad de la luz es
ID:(12682, 0)
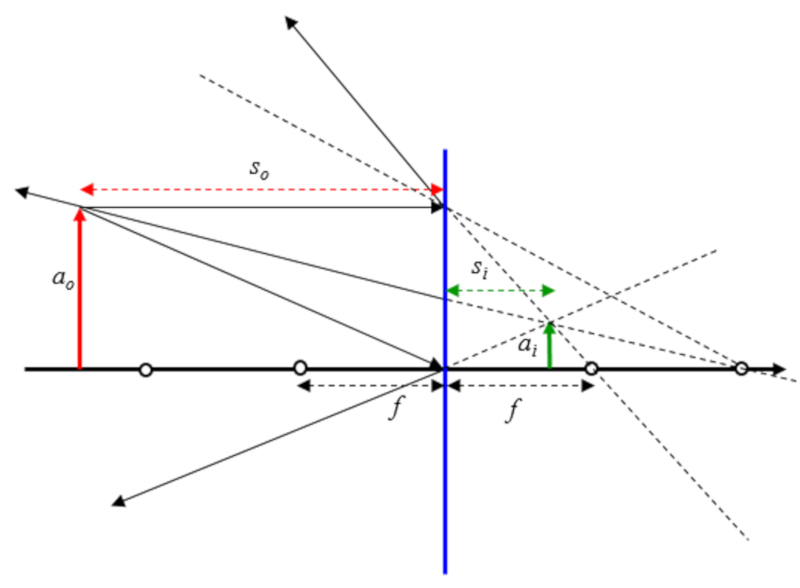
Espejo convexo con objeto mas lejos que el doble del foco
Imagen
Si se asume que el objeto esta entre el origen esta mas lejos que el doble del foco se tiene:
ID:(12689, 0)
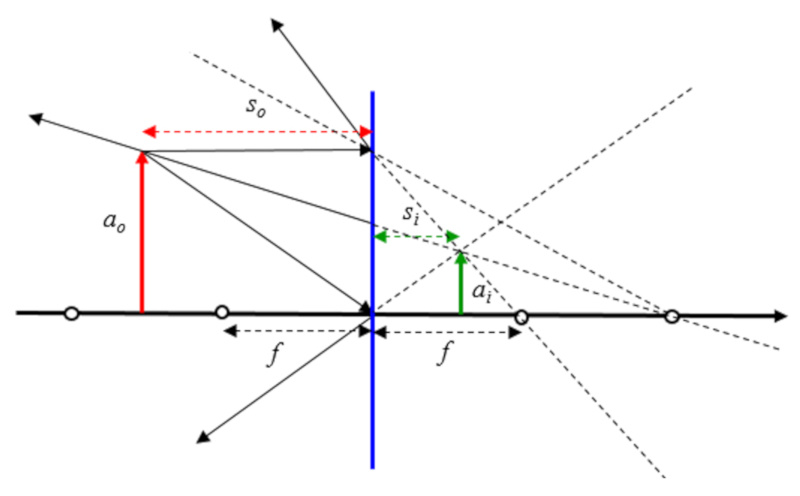
Espejo convexo con objeto entre el foco y el doble del foco
Imagen
Si se asume que el objeto esta entre el origen del foco y el doble del foco se tiene:
ID:(12688, 0)
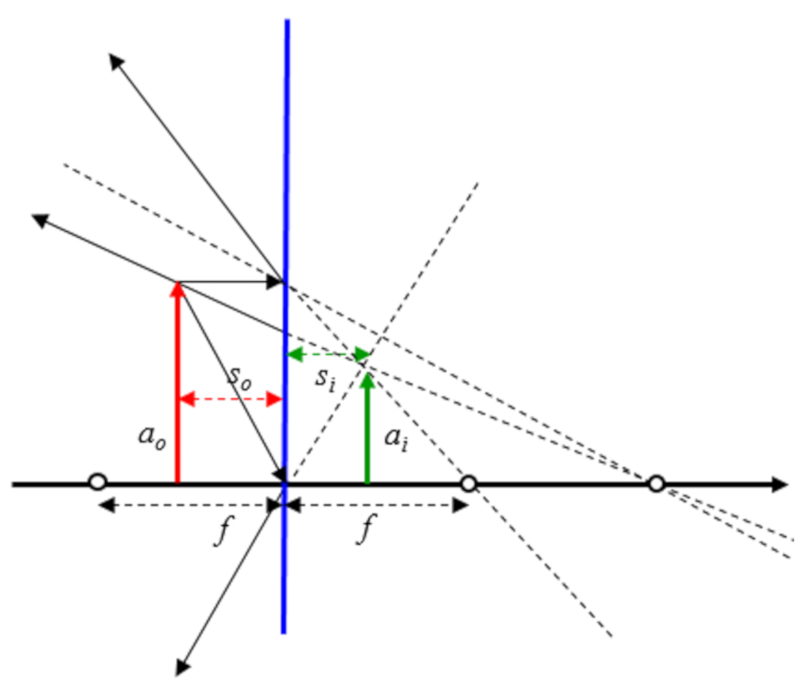
Espejo convexo con objeto entre origen y foco
Imagen
Si se asume que el objeto esta entre el origen del eje óptico y el foco se tiene:
ID:(12687, 0)
Similitud tamaños y posiciones
Imagen
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños con posiciones
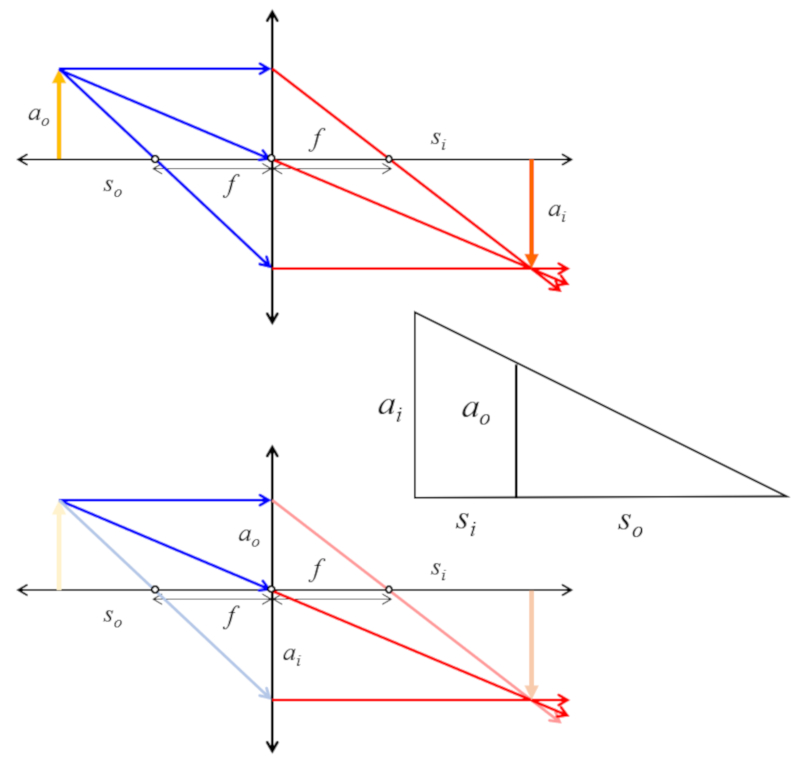
ID:(12697, 0)
Similitud tamaños, posición de objeto y foco
Imagen
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños, posición del objeto y foco:
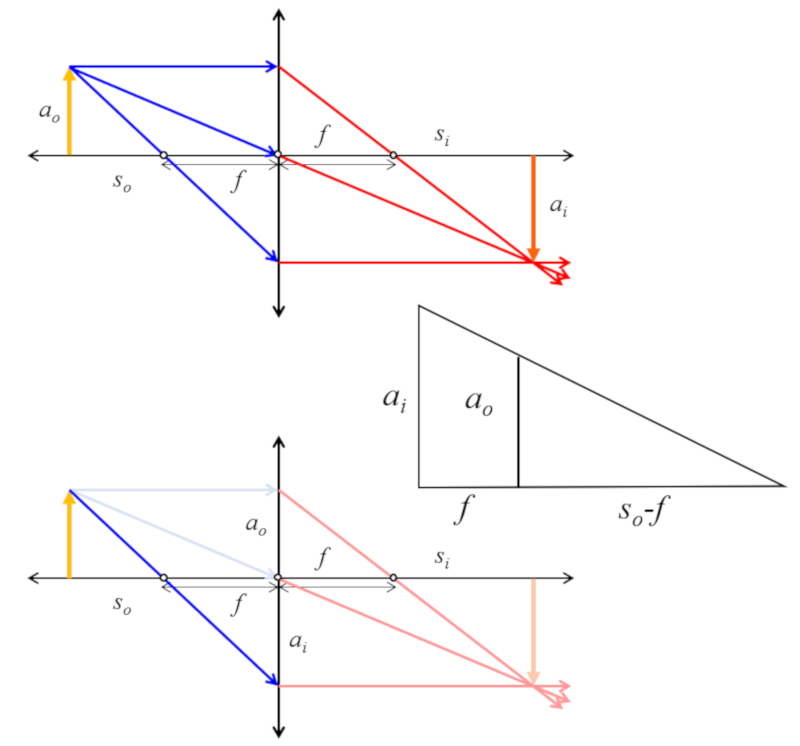
ID:(12698, 0)
Simulación de un espejo convexo
Descripción
La forma como opera el espejoe se puede simular con
ID:(12704, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$\displaystyle\frac{ s_{mv} }{ s_o }=\displaystyle\frac{ a_{mv} }{ a_o }$
s_mv / s_o = a_mv / a_o
$\displaystyle\frac{1}{ f_{mv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{mv} }$
1/ f_mv =1/ s_o + 1/ s_mv
ID:(16060, 0)
Proporciones de tamaño y posición de espejos convexo
Ecuación
La relación entre la proporción de los tamaños y posiciones cumple:
| $\displaystyle\frac{ s_{mv} }{ s_o }=\displaystyle\frac{ a_{mv} }{ a_o }$ |
ID:(12702, 0)
Posición y foco en espejo convexo
Ecuación
Las posiciones de objeto e imagen y el foco se relacionan según la ecuación:
| $\displaystyle\frac{1}{ f_{mv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{mv} }$ |
Por similitud de triangular se tiene que\\n\\n
$\displaystyle\frac{a_{mv}}{a_0}=\displaystyle\frac{f}{s_0-f}$
Con la relación
| $\displaystyle\frac{ s_{mv} }{ s_o }=\displaystyle\frac{ a_{mv} }{ a_o }$ |
\\n\\nse obtiene\\n\\n
$\displaystyle\frac{s_{mv}}{s_0}=\displaystyle\frac{f}{s_0-f}$
lo que se puede escribir como
| $\displaystyle\frac{1}{ f_{mv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{mv} }$ |
ID:(12701, 0)
0
Video
Video: Espejo Cónvexo