Konvexer Spiegel
Storyboard 
Bei einem konvexen Spiegel werden Einfallswinkel und Reflexionswinkel auf der Grundlage einer Linie bestimmt, die vom Auftreffpunkt bis zu einem Punkt verläuft, der zwei Brennweiten von der Linse hinter dem Spiegel entfernt ist.
Ein Sonderfall ist ein parallel zur optischen Achse verlaufender Strahl, der reflektiert wird, als stamme er von einem Brennpunkt hinter dem Spiegel. Umgekehrt, wenn es in Richtung des Fokus hinter dem Spiegel geht, wird es parallel zur optischen Achse reflektiert. Letzteres wird in Weitwinkelspiegeln verwendet, um 'um Ecken' zu sehen.
ID:(1265, 0)
Calculo de imagen para espejos convexo
Definition 
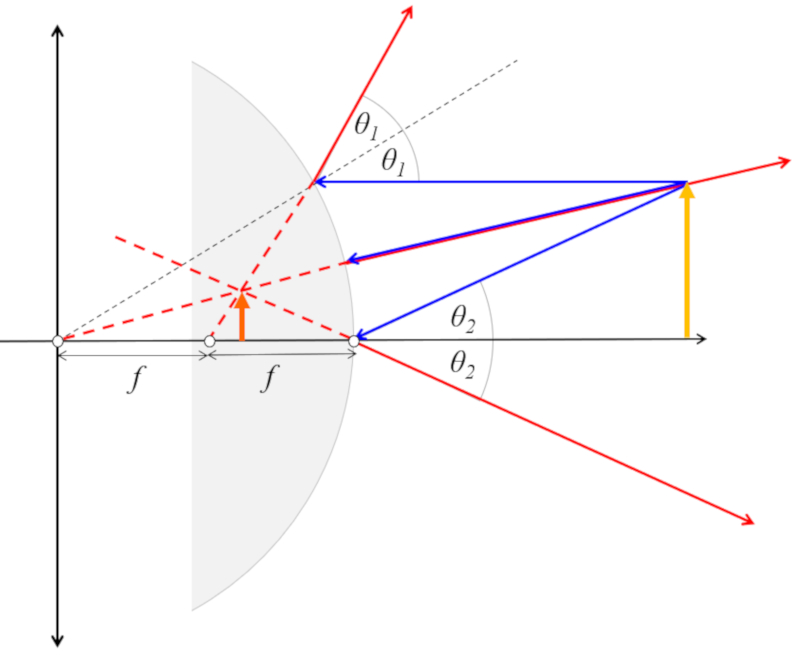
Para poder calcular el tamaño y el lugar en que se presentara la imagen se puede dibujar el eje óptico, el espejo convexo y un objeto en una posición y de un tamaño. Sobre este esquema se pueden dibujar tres haces:
• Un haz paralelo al eje óptico que se refleja de modo de que el angulo de incidencia y el de reflexión son iguales. El angulo de incidencia se determina entre la dirección del haz y una linea del punto de incidencia y el doble del foco (2f). Por ello el haz que se refleja pasa por el foco del espejo.
• Un haz que va en dirección del centro de curvatura del espejo se refleja en la misma dirección por el hecho que esta dirección es normal a la superficie.
• Un haz que pasa por un punto a una distancia igual al doble del foco se refleja por el mismo punto de incidencia volviendo a la fuente. Esto porque un haz por este punto incide perpendicular sobre la superficie por lo que se refleja en la misma dirección.
Si se dibuja correctamente los tres haces se cruzaran en un punto. Dicho punto corresponde a la imagen que se crea ya que todos los haces emanan de esta. Del punto se tiene la posición, el tamaño de la imagen y si esta invertida o no.
ID:(12682, 0)
Espejo convexo con objeto mas lejos que el doble del foco
Bild 
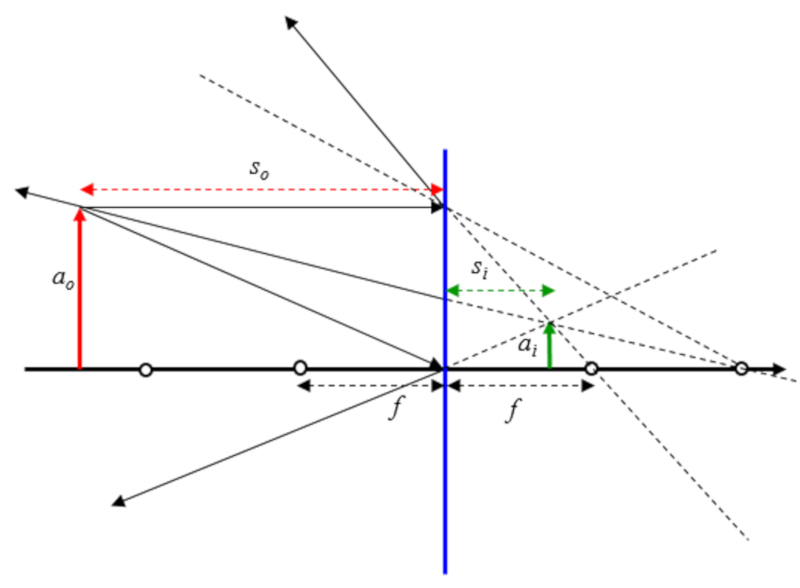
Si se asume que el objeto esta entre el origen esta mas lejos que el doble del foco se tiene:
ID:(12689, 0)
Espejo convexo con objeto entre el foco y el doble del foco
Notiz 
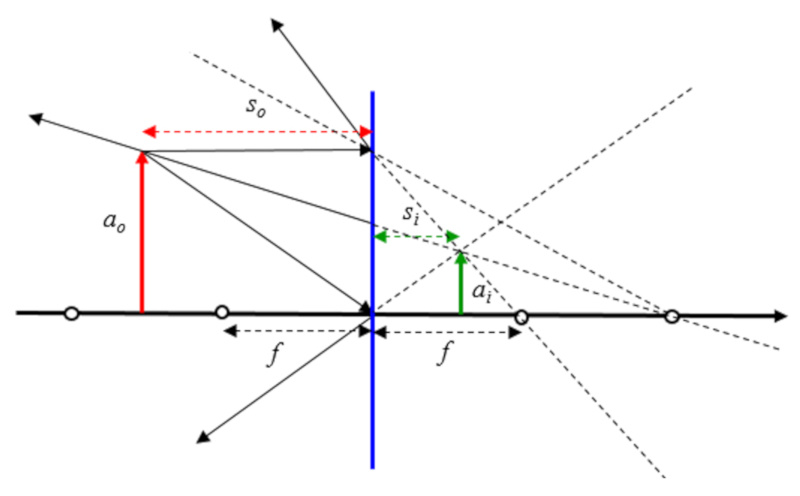
Si se asume que el objeto esta entre el origen del foco y el doble del foco se tiene:
ID:(12688, 0)
Espejo convexo con objeto entre origen y foco
Zitat 
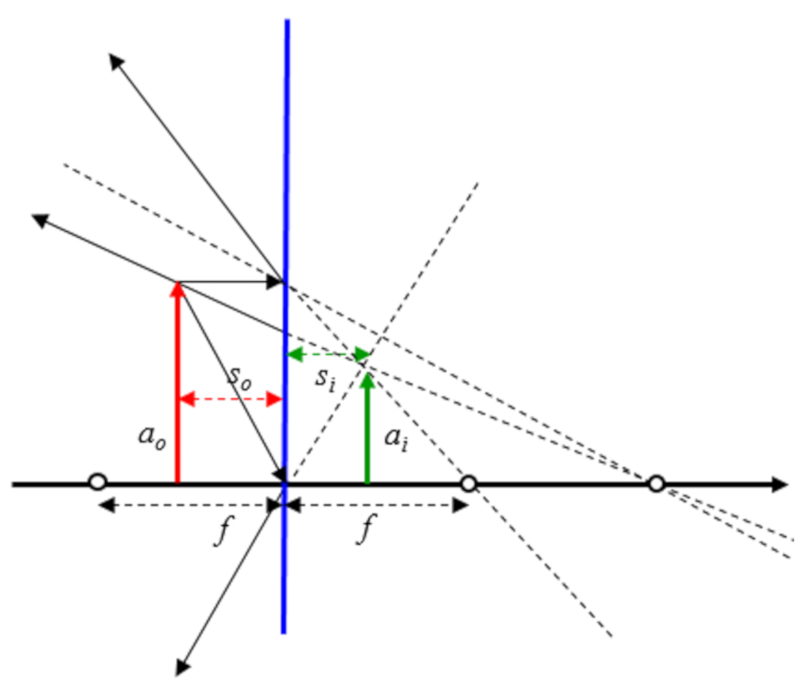
Si se asume que el objeto esta entre el origen del eje óptico y el foco se tiene:
ID:(12687, 0)
Similitud tamaños y posiciones
Übung 
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños con posiciones
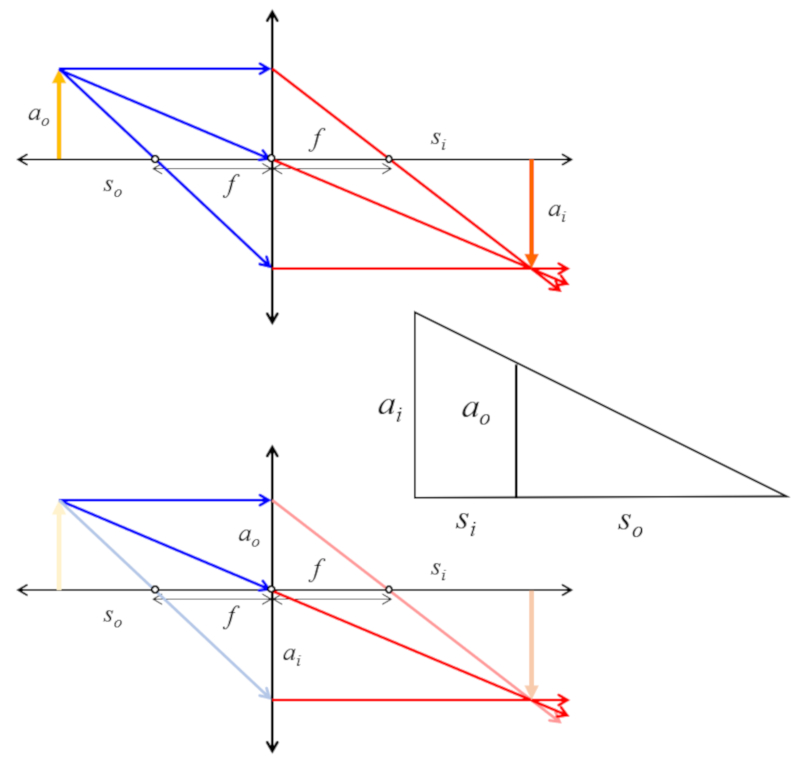
ID:(12697, 0)
Similitud tamaños, posición de objeto y foco
Gleichung 
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños, posición del objeto y foco:
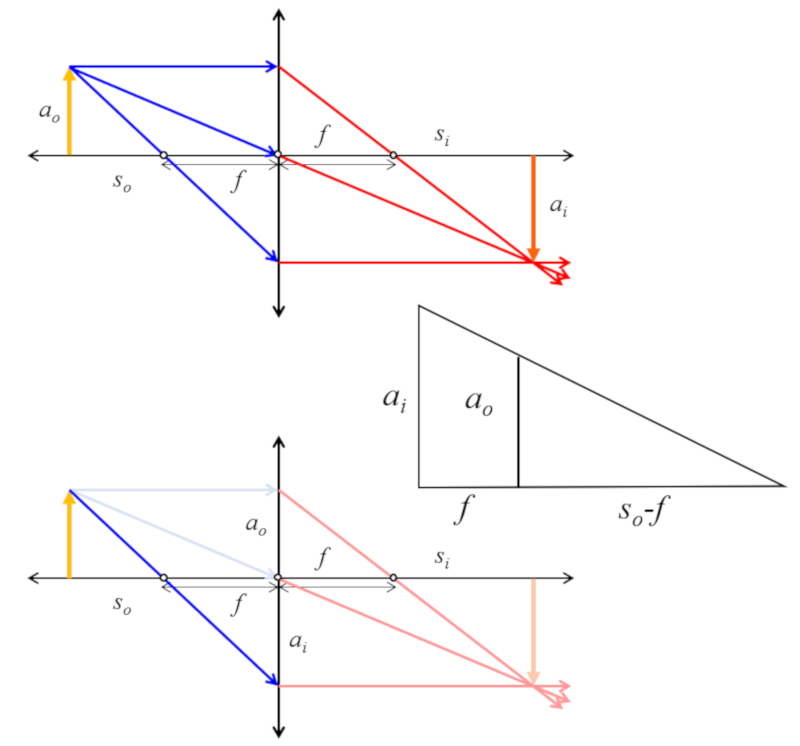
ID:(12698, 0)
Simulación de un espejo convexo
Script 
La forma como opera el espejoe se puede simular con
ID:(12704, 0)
Konvexer Spiegel
Beschreibung 
Bei einem konvexen Spiegel werden Einfallswinkel und Reflexionswinkel auf der Grundlage einer Linie bestimmt, die vom Auftreffpunkt bis zu einem Punkt verläuft, der zwei Brennweiten von der Linse hinter dem Spiegel entfernt ist. Ein Sonderfall ist ein parallel zur optischen Achse verlaufender Strahl, der reflektiert wird, als stamme er von einem Brennpunkt hinter dem Spiegel. Umgekehrt, wenn es in Richtung des Fokus hinter dem Spiegel geht, wird es parallel zur optischen Achse reflektiert. Letzteres wird in Weitwinkelspiegeln verwendet, um 'um Ecken' zu sehen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Beispiele
(ID 16068)
Para poder calcular el tama o y el lugar en que se presentara la imagen se puede dibujar el eje ptico, el espejo convexo y un objeto en una posici n y de un tama o. Sobre este esquema se pueden dibujar tres haces:
• Un haz paralelo al eje ptico que se refleja de modo de que el angulo de incidencia y el de reflexi n son iguales. El angulo de incidencia se determina entre la direcci n del haz y una linea del punto de incidencia y el doble del foco (2f). Por ello el haz que se refleja pasa por el foco del espejo.
• Un haz que va en direcci n del centro de curvatura del espejo se refleja en la misma direcci n por el hecho que esta direcci n es normal a la superficie.
• Un haz que pasa por un punto a una distancia igual al doble del foco se refleja por el mismo punto de incidencia volviendo a la fuente. Esto porque un haz por este punto incide perpendicular sobre la superficie por lo que se refleja en la misma direcci n.
Si se dibuja correctamente los tres haces se cruzaran en un punto. Dicho punto corresponde a la imagen que se crea ya que todos los haces emanan de esta. Del punto se tiene la posici n, el tama o de la imagen y si esta invertida o no.

(ID 12682)
Si se asume que el objeto esta entre el origen esta mas lejos que el doble del foco se tiene:

(ID 12689)
Si se asume que el objeto esta entre el origen del foco y el doble del foco se tiene:

(ID 12688)
Si se asume que el objeto esta entre el origen del eje ptico y el foco se tiene:

(ID 12687)
Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os con posiciones

(ID 12697)
Si se consideran los tri ngulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relaci n de tama os, posici n del objeto y foco:

(ID 12698)
La forma como opera el espejoe se puede simular con
(ID 12704)
(ID 16060)
La relaci n entre la proporci n de los tama os y posiciones cumple:
| $\displaystyle\frac{ s_{mv} }{ s_o }=\displaystyle\frac{ a_{mv} }{ a_o }$ |
(ID 12702)
Las posiciones de objeto e imagen y el foco se relacionan seg n la ecuaci n:
| $\displaystyle\frac{1}{ f_{mv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{mv} }$ |
(ID 12701)
ID:(1265, 0)
