Storyboard

Si, pendant un mouvement à vitesse angulaire constante, il se produit un changement dans cette vitesse, cela donne lieu à un mouvement qui se produit en deux étapes, chacune caractérisée par une vitesse angulaire définie.

Chaque étape est modélisée par une relation linéaire représentée par une droite, où la clé réside dans le fait que le temps et l'angle final de la première étape sont, à leur tour, le temps et l'angle initial de la deuxième étape.

Il est important de noter que ce modèle présente un problème : la vitesse angulaire change de manière instantanée, ce qui équivaut à une accélération angulaire suivie d'un freinage infini, ce qui n'est pas réaliste. Cependant, ce problème n'est pas pertinent si la durée des étapes est considérablement plus longue que le temps pendant lequel le changement de vitesse angulaire se produit.

>Modèle

ID:(1410, 0)

Iframe

>Top

ID:(15410, 0)

Concept

>Top

Un objet peut se déplacer jusqu'à A vitesse angulaire du premier étage ($\omega_1$), puis passer à un état a vitesse angulaire du deuxième étage ($\omega_2$). Ainsi, il entre dans une nouvelle phase, nécessitant une description mathématique des deux pour prédire son mouvement.

La clé réside dans le fait de reconnaître que les deux phases ont un point commun caractérisé par :

• L'angle final de la première phase et le début de la deuxième phase, le début du premier angle final et de la deuxième étape ($\theta_1$).
• Le temps final de la première phase et le début de la deuxième phase, le temps final de la première et départ de la deuxième étape ($t_1$).

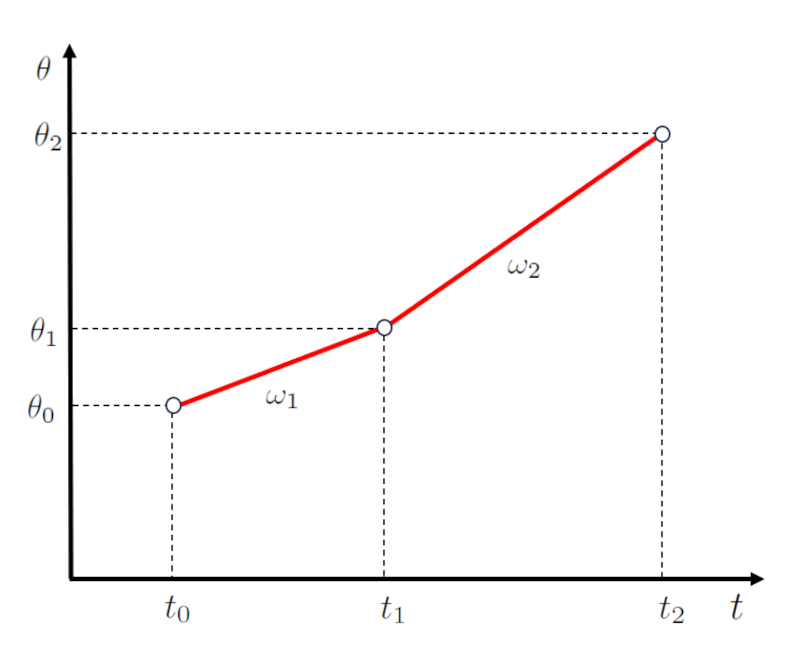
Ainsi, les graphiques d'angle en fonction du temps peuvent être combinés comme dans la représentation suivante :

Il présente un point de départ de la première étape caractérisé par le angle de départ ($\theta_0$) et le temps initial ($t_0$), et un point final de la deuxième étape caractérisé par a angle final de la deuxième étape ($\theta_2$) et le heure de fin de la deuxième étape ($t_2$).

ID:(12518, 0)

Concept

>Top

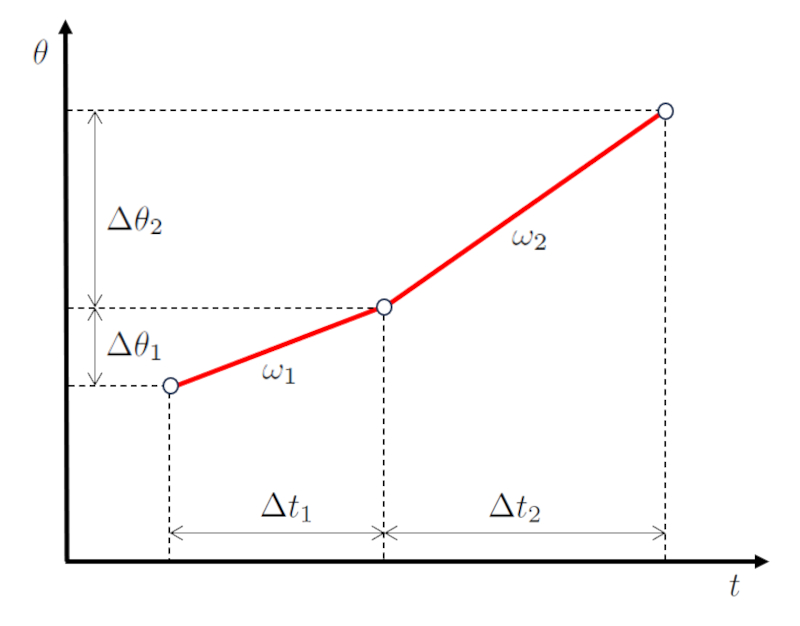
Dans un scénario de mouvement en deux étapes, d'abord l'objet avance de un angle parcouru dans la première étape ($\Delta\theta_1$) pendant un temps écoulé dans la première étape ($\Delta t_1$) avec une vitesse angulaire du premier étage ($\omega_1$).

Ensuite, dans la deuxième étape, il avance de un angle parcouru dans la deuxième étape ($\Delta\theta_2$) pendant un temps passé dans la deuxième étape ($\Delta t_2$) avec une vitesse angulaire du deuxième étage ($\omega_2$).

En représentant cela graphiquement, nous obtenons un diagramme d'angle et de temps comme illustré ci-dessous :

La clé ici est que les valeurs le temps écoulé dans la première étape ($\Delta t_1$) et le temps passé dans la deuxième étape ($\Delta t_2$) sont séquentielles, tout comme les valeurs le angle parcouru dans la première étape ($\Delta\theta_1$) et le angle parcouru dans la deuxième étape ($\Delta\theta_2$).

ID:(12525, 0)

Description

>Top

Dans le cas d'un mouvement en deux étapes, la première étape peut être décrite par une fonction impliquant les points le temps initial ($t_0$), le temps final de la première et départ de la deuxième étape ($t_1$), le angle de départ ($\theta_0$) et le début du premier angle final et de la deuxième étape ($\theta_1$), représentée par une droite avec une pente de a vitesse angulaire du premier étage ($\omega_1$) :

Pour la deuxième étape, définie par les points le début du premier angle final et de la deuxième étape ($\theta_1$), a angle final de la deuxième étape ($\theta_2$), le temps final de la première et départ de la deuxième étape ($t_1$) et le heure de fin de la deuxième étape ($t_2$), une deuxième droite avec une pente de a vitesse angulaire du deuxième étage ($\omega_2$) est utilisée :

qui est représentée comme suit :

Il est important de noter que le début de la deuxième étape, défini par les points le temps final de la première et départ de la deuxième étape ($t_1$) et le début du premier angle final et de la deuxième étape ($\theta_1$), coïncide avec la fin de la première étape.

ID:(12517, 0)

Top

>Top

Paramètres

$\theta_0$

theta_0

Angle de départ

rad

$\theta_1$

theta_1

Début du premier angle final et de la deuxième étape

rad

$r$

r

Radio

m

$t_0$

t_0

Temps initial

s

Variables

$\theta_2$

theta_2

Angle final de la deuxième étape

rad

$\Delta\theta_2$

Dtheta_2

Angle parcouru dans la deuxième étape

rad

$\Delta\theta_1$

Dtheta_1

Angle parcouru dans la première étape

rad

$\Delta\theta$

Dtheta

Différence d'angles

rad

$t_2$

t_2

Heure de fin de la deuxième étape

s

$\Delta t_1$

Dt_1

Temps écoulé dans la première étape

s

$t_1$

t_1

Temps final de la première et départ de la deuxième étape

s

$\Delta t_2$

Dt_2

Temps passé dans la deuxième étape

s

$\omega_2$

omega_2

Vitesse angulaire du deuxième étage

rad/s

$\omega_1$

omega_1

Vitesse angulaire du premier étage

rad/s

$v_2$

v_2

Vitesse du deuxième étage

m/s

$v_1$

v_1

Vitesse du premier étage

m/s

Calculs

• Méthode alternative
• Méthode traditionnelle
• Stratégie
• 2D
• 3D

Équation

Nombre

D'abord, sélectionnez l'équation: à , puis, sélectionnez la variable: à

---

Calculs

Symbole

Équation

Résolu

Traduit

Calculs

Symbole

Équation

Résolu

Traduit

Variable Donnée Calculer Cible : Équation À utiliser

Équations

ID:(15421, 0)

Équation

>Top, >Modèle

Pour décrire la rotation d'un objet, nous devons déterminer a variation d'angle ($\Delta\theta$). Cela se fait en soustrayant le angle de départ ($\theta_0$) de le angle ($\theta$), la valeur atteinte par l'objet pendant sa rotation:

$\Delta\theta = \theta_1 - \theta_0$

$\Delta\theta = \theta - \theta_0$

Conditions

Variables

$\theta$

$\theta_1$

Début du premier angle final et de la deuxième étape

$rad$

8692

$\theta_0$

Angle de départ

$rad$

5296

$\Delta\theta$

Différence d'angles

$rad$

5299

Relation

ID:(3680, 1)

Équation

>Top, >Modèle

Pour décrire la rotation d'un objet, nous devons déterminer a variation d'angle ($\Delta\theta$). Cela se fait en soustrayant le angle de départ ($\theta_0$) de le angle ($\theta$), la valeur atteinte par l'objet pendant sa rotation:

$\Delta\theta = \theta_2 - \theta_1$

$\Delta\theta = \theta - \theta_0$

Conditions

Variables

$\theta$

$\theta_2$

Angle final de la deuxième étape

$rad$

10302

$\theta_0$

$\theta_1$

Début du premier angle final et de la deuxième étape

$rad$

8692

$\Delta\theta$

Différence d'angles

$rad$

5299

Relation

ID:(3680, 2)

Équation

>Top, >Modèle

Pour décrire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La durée est déterminée en soustrayant le temps initial du temps final :

$\Delta t_1 \equiv t_1 - t_0$

$\Delta t \equiv t - t_0$

Conditions

Variables

$t$

$t_1$

Temps final de la première et départ de la deuxième étape

$s$

10240

$\Delta t$

$\Delta t_1$

Temps écoulé dans la première étape

$s$

10242

$t_0$

Temps initial

$s$

5265

Relation

ID:(4353, 1)

Équation

>Top, >Modèle

Pour décrire le mouvement d'un objet, nous devons calculer le temps écoulé ($\Delta t$). Cette grandeur est obtenue en mesurant le temps initial ($t_0$) et le le temps ($t$) de ce mouvement. La durée est déterminée en soustrayant le temps initial du temps final :

$\Delta t_2 \equiv t_2 - t_1$

$\Delta t \equiv t - t_0$

Conditions

Variables

$t$

$t_2$

Heure de fin de la deuxième étape

$s$

10241

$\Delta t$

$\Delta t_2$

Temps passé dans la deuxième étape

$s$

10243

$t_0$

$t_1$

Temps final de la première et départ de la deuxième étape

$s$

10240

Relation

ID:(4353, 2)

Équation

>Top, >Modèle

Dans le cas où la vitesse angulaire est constante, a vitesse angulaire moyenne ($\bar{\omega}$) coïncide avec la valeur de a vitesse angulaire initiale ($\omega_0$), donc

Dans ce scénario, nous pouvons calculer l'angle parcouru en fonction du temps en rappelant qu'il est associé à la différence entre les angles actuel et initial, ainsi qu'entre le temps actuel et initial. Par conséquent, le angle ($\theta$) est égal à Le angle de départ ($\theta_0$), a vitesse angulaire initiale ($\omega_0$), le temps ($t$) et le temps initial ($t_0$) comme indiqué ci-dessous :

$\theta_1 = \theta_0 + \omega_1 ( t_1 - t_0 )$

$\theta = \theta_0 + \omega_0 ( t - t_0 )$

Conditions

Variables

$\theta$

$\theta_1$

Début du premier angle final et de la deuxième étape

$rad$

8692

$\theta_0$

Angle de départ

$rad$

5296

$t$

$t_1$

Temps final de la première et départ de la deuxième étape

$s$

10240

$t_0$

Temps initial

$s$

5265

$\omega_0$

$\omega_1$

Vitesse angulaire du premier étage

$rad/s$

10303

Relation

Développement

Dans le cas où A vitesse angulaire initiale ($\omega_0$) est égal à A vitesse angulaire moyenne ($\bar{\omega}$),

$\bar{\omega} = \omega_0$

Par conséquent, avec a différence d'angles ($\Delta\theta$), qui est égal à Le angle ($\theta$) divisé par le angle de départ ($\theta_0$), nous obtenons :

$\Delta\theta = \theta - \theta_0$

Et avec le temps écoulé ($\Delta t$), qui est égal à Le temps ($t$) divisé par le temps initial ($t_0$), nous obtenons :

$\Delta t \equiv t - t_0$

Nous pouvons réécrire l'équation pour a vitesse angulaire moyenne ($\bar{\omega}$) comme suit :

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Cela peut être exprimé comme suit :

$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$

En résolvant cela, nous obtenons :

$\theta = \theta_0 + \omega_0 ( t - t_0 )$

L'équation représente une droite dans l'espace angle-temps.

ID:(1023, 1)

Équation

>Top, >Modèle

Dans le cas où la vitesse angulaire est constante, a vitesse angulaire moyenne ($\bar{\omega}$) coïncide avec la valeur de a vitesse angulaire initiale ($\omega_0$), donc

Dans ce scénario, nous pouvons calculer l'angle parcouru en fonction du temps en rappelant qu'il est associé à la différence entre les angles actuel et initial, ainsi qu'entre le temps actuel et initial. Par conséquent, le angle ($\theta$) est égal à Le angle de départ ($\theta_0$), a vitesse angulaire initiale ($\omega_0$), le temps ($t$) et le temps initial ($t_0$) comme indiqué ci-dessous :

$\theta_2 = \theta_1 + \omega_2 ( t_2 - t_1 )$

$\theta = \theta_0 + \omega_0 ( t - t_0 )$

Conditions

Variables

$\theta$

$\theta_2$

Angle final de la deuxième étape

$rad$

10302

$\theta_0$

$\theta_1$

Début du premier angle final et de la deuxième étape

$rad$

8692

$t$

$t_2$

Heure de fin de la deuxième étape

$s$

10241

$t_0$

$t_1$

Temps final de la première et départ de la deuxième étape

$s$

10240

$\omega_0$

$\omega_2$

Vitesse angulaire du deuxième étage

$rad/s$

10304

Relation

Développement

Dans le cas où A vitesse angulaire initiale ($\omega_0$) est égal à A vitesse angulaire moyenne ($\bar{\omega}$),

$\bar{\omega} = \omega_0$

Par conséquent, avec a différence d'angles ($\Delta\theta$), qui est égal à Le angle ($\theta$) divisé par le angle de départ ($\theta_0$), nous obtenons :

$\Delta\theta = \theta - \theta_0$

Et avec le temps écoulé ($\Delta t$), qui est égal à Le temps ($t$) divisé par le temps initial ($t_0$), nous obtenons :

$\Delta t \equiv t - t_0$

Nous pouvons réécrire l'équation pour a vitesse angulaire moyenne ($\bar{\omega}$) comme suit :

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Cela peut être exprimé comme suit :

$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$

En résolvant cela, nous obtenons :

$\theta = \theta_0 + \omega_0 ( t - t_0 )$

L'équation représente une droite dans l'espace angle-temps.

ID:(1023, 2)

Équation

>Top, >Modèle

Pour estimer le déplacement d'un objet, il est nécessaire de connaître sa a vitesse angulaire ($\omega$) en fonction de le temps ($t$). Ainsi, on introduit la a vitesse angulaire moyenne ($\bar{\omega}$), définie comme le rapport entre a variation d'angle ($\Delta\theta$) et le temps écoulé ($\Delta t$).

Pour mesurer cela, on peut utiliser un système comme celui illustré sur l'image :

Pour déterminer la vitesse angulaire moyenne, on place un élément réfléchissant sur l\'axe ou sur un disque avec plusieurs éléments réfléchissants, et on enregistre le passage pour estimer la longueur de l\'arc $\Delta s$ et l\'angle associé au rayon $r$. Ensuite, la différence de temps lorsque la marque passe devant le capteur est enregistrée comme $\Delta t$. La vitesse angulaire moyenne est déterminée en divisant l\'angle parcouru par le temps écoulé.

L\'équation qui décrit la vitesse angulaire moyenne est :

$\omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Conditions

Variables

$\Delta\theta$

$\Delta\theta_1$

Angle parcouru dans la première étape

$rad$

10305

$\Delta t$

$\Delta t_1$

Temps écoulé dans la première étape

$s$

10242

$\bar{\omega}$

$\omega_1$

Vitesse angulaire du premier étage

$rad/s$

10303

Relation

Développement

La définition de a vitesse angulaire moyenne ($\bar{\omega}$) est considérée comme a variation d'angle ($\Delta\theta$),

$\Delta\theta = \theta - \theta_0$

et le temps écoulé ($\Delta t$),

$\Delta t \equiv t - t_0$

La relation entre les deux est définie comme a vitesse angulaire moyenne ($\bar{\omega}$) :

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Il convient de noter que la vitesse moyenne est une estimation de la vitesse angulaire réelle. Le principal problème est que :

Si la vitesse angulaire varie pendant le temps écoulé, la valeur de la vitesse angulaire moyenne peut être très différente de la vitesse angulaire moyenne.

Par conséquent, la clé est :

Déterminer la vitesse dans un temps écoulé suffisamment court pour minimiser sa variation.

ID:(3679, 1)

Équation

>Top, >Modèle

Pour estimer le déplacement d'un objet, il est nécessaire de connaître sa a vitesse angulaire ($\omega$) en fonction de le temps ($t$). Ainsi, on introduit la a vitesse angulaire moyenne ($\bar{\omega}$), définie comme le rapport entre a variation d'angle ($\Delta\theta$) et le temps écoulé ($\Delta t$).

Pour mesurer cela, on peut utiliser un système comme celui illustré sur l'image :

Pour déterminer la vitesse angulaire moyenne, on place un élément réfléchissant sur l\'axe ou sur un disque avec plusieurs éléments réfléchissants, et on enregistre le passage pour estimer la longueur de l\'arc $\Delta s$ et l\'angle associé au rayon $r$. Ensuite, la différence de temps lorsque la marque passe devant le capteur est enregistrée comme $\Delta t$. La vitesse angulaire moyenne est déterminée en divisant l\'angle parcouru par le temps écoulé.

L\'équation qui décrit la vitesse angulaire moyenne est :

$\omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Conditions

Variables

$\Delta\theta$

$\Delta\theta_2$

Angle parcouru dans la deuxième étape

$rad$

10306

$\Delta t$

$\Delta t_2$

Temps passé dans la deuxième étape

$s$

10243

$\bar{\omega}$

$\omega_2$

Vitesse angulaire du deuxième étage

$rad/s$

10304

Relation

Développement

La définition de a vitesse angulaire moyenne ($\bar{\omega}$) est considérée comme a variation d'angle ($\Delta\theta$),

$\Delta\theta = \theta - \theta_0$

et le temps écoulé ($\Delta t$),

$\Delta t \equiv t - t_0$

La relation entre les deux est définie comme a vitesse angulaire moyenne ($\bar{\omega}$) :

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Il convient de noter que la vitesse moyenne est une estimation de la vitesse angulaire réelle. Le principal problème est que :

Si la vitesse angulaire varie pendant le temps écoulé, la valeur de la vitesse angulaire moyenne peut être très différente de la vitesse angulaire moyenne.

Par conséquent, la clé est :

Déterminer la vitesse dans un temps écoulé suffisamment court pour minimiser sa variation.

ID:(3679, 2)

Équation

>Top, >Modèle

Si nous divisons la relation entre a distance parcourue en un temps ($\Delta s$) et le radio ($r$) par a variation d'angle ($\Delta\theta$),

et puis la divisons par le temps écoulé ($\Delta t$), nous obtenons la relation qui nous permet de calculer a vitesse ($v$) le long de l'orbite, connue sous le nom de vitesse tangentielle, qui est associée à A vitesse angulaire ($\omega$):

$v_1 = r \omega_1$

$v = r \omega$

Conditions

Variables

$r$

Radio

$m$

9894

$v$

$v_1$

Vitesse du premier étage

$m/s$

10238

$\omega$

$\omega_1$

Vitesse angulaire du premier étage

$rad/s$

10303

Relation

Développement

Comme a vitesse moyenne ($\bar{v}$) est avec a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$), égal à

$\bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$

et avec a distance parcourue en un temps ($\Delta s$) exprimé comme un arc de cercle, et le radio ($r$) et a variation d'angle ($\Delta\theta$) sont

$\Delta s=r \Delta\theta$

et la définition de a vitesse angulaire moyenne ($\bar{\omega}$) est

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

alors,

$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$

Comme la relation est générale, elle peut être appliquée pour des valeurs instantanées, ce qui donne

$v = r \omega$

ID:(3233, 1)

Équation

>Top, >Modèle

Si nous divisons la relation entre a distance parcourue en un temps ($\Delta s$) et le radio ($r$) par a variation d'angle ($\Delta\theta$),

et puis la divisons par le temps écoulé ($\Delta t$), nous obtenons la relation qui nous permet de calculer a vitesse ($v$) le long de l'orbite, connue sous le nom de vitesse tangentielle, qui est associée à A vitesse angulaire ($\omega$):

$v_2 = r \omega_2$

$v = r \omega$

Conditions

Variables

$r$

Radio

$m$

9894

$v$

$v_2$

Vitesse du deuxième étage

$m/s$

10239

$\omega$

$\omega_2$

Vitesse angulaire du deuxième étage

$rad/s$

10304

Relation

Développement

Comme a vitesse moyenne ($\bar{v}$) est avec a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$), égal à

$\bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$

et avec a distance parcourue en un temps ($\Delta s$) exprimé comme un arc de cercle, et le radio ($r$) et a variation d'angle ($\Delta\theta$) sont

$\Delta s=r \Delta\theta$

et la définition de a vitesse angulaire moyenne ($\bar{\omega}$) est

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

alors,

$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$

Comme la relation est générale, elle peut être appliquée pour des valeurs instantanées, ce qui donne

$v = r \omega$

ID:(3233, 2)