Storyboard

Si durante un movimiento a velocidad angular constante se produce un cambio en esta, se obtiene un movimiento que ocurre en dos etapas, cada una caracterizada por una velocidad angular definida.

Cada etapa se modela con una relación lineal representada por una recta, donde la clave radica en que el tiempo y el ángulo final de la primera etapa son, a su vez, el tiempo y el ángulo inicial de la segunda etapa.

Es importante destacar que este modelo presenta un problema: la velocidad angular cambia de forma instantánea, lo que equivale a una aceleración angular seguida de un frenado infinito, lo cual no es realista. Sin embargo, este problema no resulta relevante si la duración de las etapas es considerablemente más larga que el tiempo en el que ocurre el cambio de velocidad angular.

>Modelo

ID:(1410, 0)

Iframe

>Top

ID:(15410, 0)

Concepto

>Top

Un cuerpo se puede desplazar a la velocidad ángular primera etapa ($\omega_1$) y luego pasa a una la velocidad angular segunda etapa ($\omega_2$). Con ello, entra en una nueva etapa, siendo necesario describir ambas en forma matemática para predecir su movimiento.

La clave es observar que ambas etapas tienen un punto en común caracterizado por:

• El ángulo final de la primera etapa e inicio de la segunda, el ángulo final primera e inició segunda etapa ($\theta_1$).
• El tiempo final de la primera etapa e inicio de la segunda, el tiempo final primera e inició segunda etapa ($t_1$).
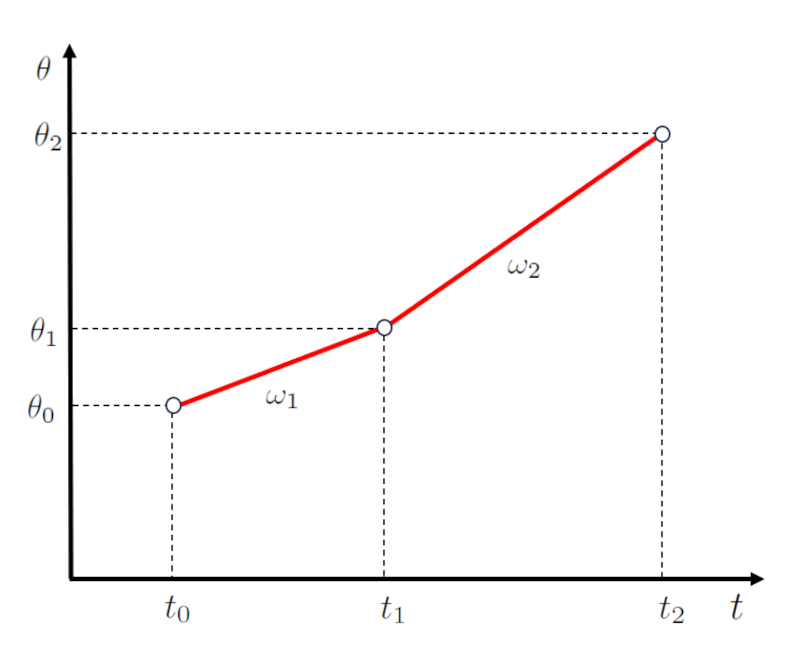
Así, los diagramas del ángulo en función del tiempo pueden acoplarse como se muestra en la siguiente representación:

En ella se encuentra un punto inicial de la primera etapa caracterizado por el ángulo inicial ($\theta_0$) y el tiempo inicial ($t_0$), y el punto final de la segunda etapa caracterizado por la ángulo final segunda etapa ($\theta_2$) y el tiempo que finaliza segunda etapa ($t_2$).

ID:(12518, 0)

Concepto

>Top

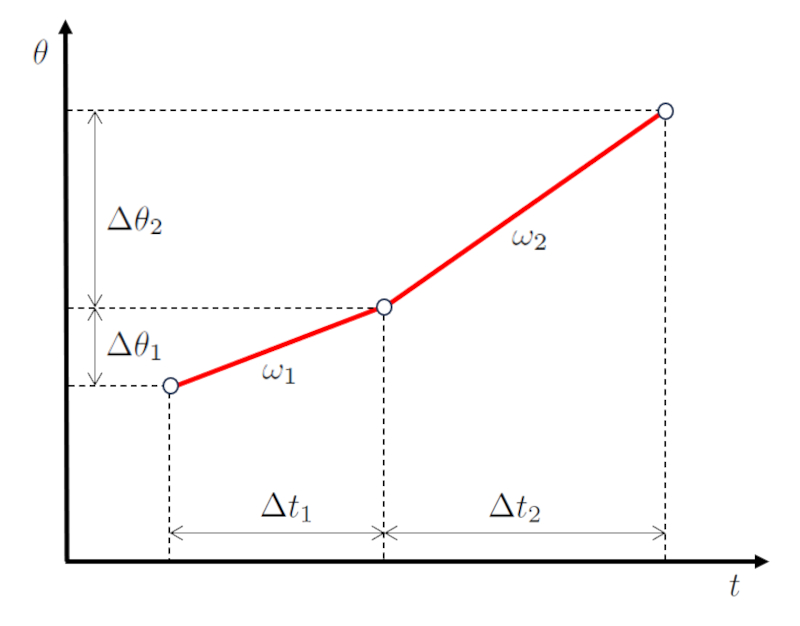
En un escenario de movimiento en dos etapas, primero el objeto avanza un ángulo recorrido en la primera etapa ($\Delta\theta_1$) durante un tiempo transcurrido en la primera etapa ($\Delta t_1$) con una velocidad ángular primera etapa ($\omega_1$).

Posteriormente, en la segunda etapa, avanza un ángulo recorrido en la segunda etapa ($\Delta\theta_2$) durante un tiempo transcurrido en la segunda etapa ($\Delta t_2$) con una velocidad angular segunda etapa ($\omega_2$).

Al representar esto gráficamente, obtenemos un diagrama de ángulo y tiempo como se muestra a continuación:

La clave aquí es que los valores el tiempo transcurrido en la primera etapa ($\Delta t_1$) y el tiempo transcurrido en la segunda etapa ($\Delta t_2$) son secuenciales, al igual que los valores el ángulo recorrido en la primera etapa ($\Delta\theta_1$) y el ángulo recorrido en la segunda etapa ($\Delta\theta_2$).

ID:(12525, 0)

Descripción

>Top

En el caso de un movimiento en dos etapas, la primera etapa puede describirse mediante una función que involucra los puntos el tiempo inicial ($t_0$), el tiempo final primera e inició segunda etapa ($t_1$), el ángulo inicial ($\theta_0$) y el ángulo final primera e inició segunda etapa ($\theta_1$), representada por una recta con una pendiente de la velocidad ángular primera etapa ($\omega_1$):

Para la segunda etapa, definida por los puntos el ángulo final primera e inició segunda etapa ($\theta_1$), la ángulo final segunda etapa ($\theta_2$), el tiempo final primera e inició segunda etapa ($t_1$) y el tiempo que finaliza segunda etapa ($t_2$), se emplea una segunda recta con una pendiente de la velocidad angular segunda etapa ($\omega_2$):

que se representa como:

Es importante notar que el inicio de la segunda etapa, definido por los puntos el tiempo final primera e inició segunda etapa ($t_1$) y el ángulo final primera e inició segunda etapa ($\theta_1$), coincide con el final de la primera etapa.

ID:(12517, 0)

Top

>Top

Parámetros

$\theta_1$

theta_1

Ángulo final primera e inició segunda etapa

rad

$\theta_0$

theta_0

Ángulo inicial

rad

$r$

r

Radio

m

$t_0$

t_0

Tiempo inicial

s

Variables

$\theta_2$

theta_2

Ángulo final segunda etapa

rad

$\Delta\theta_1$

Dtheta_1

Ángulo recorrido en la primera etapa

rad

$\Delta\theta_2$

Dtheta_2

Ángulo recorrido en la segunda etapa

rad

$\Delta\theta$

Dtheta

Diferencia de ángulos

rad

$t_1$

t_1

Tiempo final primera e inició segunda etapa

s

$t_2$

t_2

Tiempo que finaliza segunda etapa

s

$\Delta t_1$

Dt_1

Tiempo transcurrido en la primera etapa

s

$\Delta t_2$

Dt_2

Tiempo transcurrido en la segunda etapa

s

$\omega_1$

omega_1

Velocidad ángular primera etapa

rad/s

$\omega_2$

omega_2

Velocidad angular segunda etapa

rad/s

$v_1$

v_1

Velocidad primera etapa

m/s

$v_2$

v_2

Velocidad segunda etapa

m/s

Cálculos

• Método alternativo
• Método tradicional
• Estrategia
• 2D
• 3D

Ecuación

Número

Primero, seleccione la ecuación: a , luego, seleccione la variable: a

---

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable Dado Calcule Objetivo : Ecuación A utilizar

Ecuaciones

ID:(15421, 0)

Ecuación

>Top, >Modelo

Para describir la rotación de un objeto, es necesario determinar la variación del angulo ($\Delta\theta$). Esto se logra restando el ángulo inicial ($\theta_0$) del valor alcanzado por el objeto durante su rotación, que es el ángulo ($\theta$):

$\Delta\theta = \theta_1 - \theta_0$

$\Delta\theta = \theta - \theta_0$

Condiciones

Variables

$\theta$

$\theta_1$

Ángulo final primera e inició segunda etapa

$rad$

8692

$\theta_0$

Ángulo inicial

$rad$

5296

$\Delta\theta$

Diferencia de ángulos

$rad$

5299

Relación

ID:(3680, 1)

Ecuación

>Top, >Modelo

Para describir la rotación de un objeto, es necesario determinar la variación del angulo ($\Delta\theta$). Esto se logra restando el ángulo inicial ($\theta_0$) del valor alcanzado por el objeto durante su rotación, que es el ángulo ($\theta$):

$\Delta\theta = \theta_2 - \theta_1$

$\Delta\theta = \theta - \theta_0$

Condiciones

Variables

$\theta$

$\theta_2$

Ángulo final segunda etapa

$rad$

10302

$\theta_0$

$\theta_1$

Ángulo final primera e inició segunda etapa

$rad$

8692

$\Delta\theta$

Diferencia de ángulos

$rad$

5299

Relación

ID:(3680, 2)

Ecuación

>Top, >Modelo

Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duración se determina restando el tiempo inicial al tiempo final:

$\Delta t_1 \equiv t_1 - t_0$

$\Delta t \equiv t - t_0$

Condiciones

Variables

$t$

$t_1$

Tiempo final primera e inició segunda etapa

$s$

10240

$t_0$

Tiempo inicial

$s$

5265

$\Delta t$

$\Delta t_1$

Tiempo transcurrido en la primera etapa

$s$

10242

Relación

ID:(4353, 1)

Ecuación

>Top, >Modelo

Para describir el movimiento de un objeto, debemos calcular el tiempo transcurrido ($\Delta t$). Esta magnitud se obtiene midiendo el tiempo inicial ($t_0$) y el el tiempo ($t$) de dicho movimiento. La duración se determina restando el tiempo inicial al tiempo final:

$\Delta t_2 \equiv t_2 - t_1$

$\Delta t \equiv t - t_0$

Condiciones

Variables

$t$

$t_2$

Tiempo que finaliza segunda etapa

$s$

10241

$t_0$

$t_1$

Tiempo final primera e inició segunda etapa

$s$

10240

$\Delta t$

$\Delta t_2$

Tiempo transcurrido en la segunda etapa

$s$

10243

Relación

ID:(4353, 2)

Ecuación

>Top, >Modelo

En el caso de que la velocidad angular sea constante, la velocidad angular media ($\bar{\omega}$) coincide con el valor de la velocidad angular inicial ($\omega_0$), por lo que

En este caso, podemos calcular el ángulo recorrido en función del tiempo recordando que este se asocia a la diferencia entre el ángulo actual y el inicial, así como el tiempo actual y el inicial. Por lo tanto, el ángulo ($\theta$) es igual a el ángulo inicial ($\theta_0$), la velocidad angular inicial ($\omega_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) como se muestra a continuación:

$\theta_1 = \theta_0 + \omega_1 ( t_1 - t_0 )$

$\theta = \theta_0 + \omega_0 ( t - t_0 )$

Condiciones

Variables

$\theta$

$\theta_1$

Ángulo final primera e inició segunda etapa

$rad$

8692

$\theta_0$

Ángulo inicial

$rad$

5296

$t$

$t_1$

Tiempo final primera e inició segunda etapa

$s$

10240

$t_0$

Tiempo inicial

$s$

5265

$\omega_0$

$\omega_1$

Velocidad ángular primera etapa

$rad/s$

10303

Relación

Desarrollo

En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),

$\bar{\omega} = \omega_0$

Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:

$\Delta\theta = \theta - \theta_0$

Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:

$\Delta t \equiv t - t_0$

Podemos reescribir la ecuación de la velocidad angular media ($\bar{\omega}$) como:

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Esto se puede expresar como:

$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$

Despejando, obtenemos:

$\theta = \theta_0 + \omega_0 ( t - t_0 )$

La ecuación representa una recta en el espacio ángulo-tiempo.

ID:(1023, 1)

Ecuación

>Top, >Modelo

En el caso de que la velocidad angular sea constante, la velocidad angular media ($\bar{\omega}$) coincide con el valor de la velocidad angular inicial ($\omega_0$), por lo que

En este caso, podemos calcular el ángulo recorrido en función del tiempo recordando que este se asocia a la diferencia entre el ángulo actual y el inicial, así como el tiempo actual y el inicial. Por lo tanto, el ángulo ($\theta$) es igual a el ángulo inicial ($\theta_0$), la velocidad angular inicial ($\omega_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) como se muestra a continuación:

$\theta_2 = \theta_1 + \omega_2 ( t_2 - t_1 )$

$\theta = \theta_0 + \omega_0 ( t - t_0 )$

Condiciones

Variables

$\theta$

$\theta_2$

Ángulo final segunda etapa

$rad$

10302

$\theta_0$

$\theta_1$

Ángulo final primera e inició segunda etapa

$rad$

8692

$t$

$t_2$

Tiempo que finaliza segunda etapa

$s$

10241

$t_0$

$t_1$

Tiempo final primera e inició segunda etapa

$s$

10240

$\omega_0$

$\omega_2$

Velocidad angular segunda etapa

$rad/s$

10304

Relación

Desarrollo

En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),

$\bar{\omega} = \omega_0$

Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:

$\Delta\theta = \theta - \theta_0$

Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:

$\Delta t \equiv t - t_0$

Podemos reescribir la ecuación de la velocidad angular media ($\bar{\omega}$) como:

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Esto se puede expresar como:

$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$

Despejando, obtenemos:

$\theta = \theta_0 + \omega_0 ( t - t_0 )$

La ecuación representa una recta en el espacio ángulo-tiempo.

ID:(1023, 2)

Ecuación

>Top, >Modelo

Para estimar el desplazamiento de un objeto, es necesario conocer su la velocidad angular ($\omega$) en función de el tiempo ($t$). Por lo tanto, se introduce la la velocidad angular media ($\bar{\omega}$), definida como la proporción entre la variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$).

Para medir esto, se puede utilizar un sistema como el que se muestra en la imagen:

Para determinar la velocidad angular media, se coloca un elemento reflectante en el eje o en un disco con varios elementos reflectantes, y se registra el paso para estimar la longitud del arco $\Delta s$ y el ángulo asociado con el radio $r$. Luego se registra la diferencia de tiempo cuando la marca pasa frente al sensor como $\Delta t$. La velocidad angular media se determina dividiendo el ángulo recorrido por el tiempo transcurrido.

La ecuación que describe la velocidad angular media es:

$\omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Condiciones

Variables

$\Delta\theta$

$\Delta\theta_1$

Ángulo recorrido en la primera etapa

$rad$

10305

$\Delta t$

$\Delta t_1$

Tiempo transcurrido en la primera etapa

$s$

10242

$\bar{\omega}$

$\omega_1$

Velocidad ángular primera etapa

$rad/s$

10303

Relación

Desarrollo

La definición de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),

$\Delta\theta = \theta - \theta_0$

y el tiempo transcurrido ($\Delta t$),

$\Delta t \equiv t - t_0$

La relación entre ambos se define como la velocidad angular media ($\bar{\omega}$):

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Cabe destacar que la velocidad media es una estimación de la velocidad angular real. El problema principal es que:

Si la velocidad angular varía durante el tiempo transcurrido, el valor de la velocidad angular media puede ser muy diferente de la velocidad angular promedio.

Por lo tanto, la clave es:

Determinar la velocidad en un tiempo transcurrido suficientemente corto para minimizar su variación.

ID:(3679, 1)

Ecuación

>Top, >Modelo

Para estimar el desplazamiento de un objeto, es necesario conocer su la velocidad angular ($\omega$) en función de el tiempo ($t$). Por lo tanto, se introduce la la velocidad angular media ($\bar{\omega}$), definida como la proporción entre la variación del angulo ($\Delta\theta$) y el tiempo transcurrido ($\Delta t$).

Para medir esto, se puede utilizar un sistema como el que se muestra en la imagen:

Para determinar la velocidad angular media, se coloca un elemento reflectante en el eje o en un disco con varios elementos reflectantes, y se registra el paso para estimar la longitud del arco $\Delta s$ y el ángulo asociado con el radio $r$. Luego se registra la diferencia de tiempo cuando la marca pasa frente al sensor como $\Delta t$. La velocidad angular media se determina dividiendo el ángulo recorrido por el tiempo transcurrido.

La ecuación que describe la velocidad angular media es:

$\omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Condiciones

Variables

$\Delta\theta$

$\Delta\theta_2$

Ángulo recorrido en la segunda etapa

$rad$

10306

$\Delta t$

$\Delta t_2$

Tiempo transcurrido en la segunda etapa

$s$

10243

$\bar{\omega}$

$\omega_2$

Velocidad angular segunda etapa

$rad/s$

10304

Relación

Desarrollo

La definición de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),

$\Delta\theta = \theta - \theta_0$

y el tiempo transcurrido ($\Delta t$),

$\Delta t \equiv t - t_0$

La relación entre ambos se define como la velocidad angular media ($\bar{\omega}$):

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

Cabe destacar que la velocidad media es una estimación de la velocidad angular real. El problema principal es que:

Si la velocidad angular varía durante el tiempo transcurrido, el valor de la velocidad angular media puede ser muy diferente de la velocidad angular promedio.

Por lo tanto, la clave es:

Determinar la velocidad en un tiempo transcurrido suficientemente corto para minimizar su variación.

ID:(3679, 2)

Ecuación

>Top, >Modelo

Si dividimos la relación entre la distancia recorrida en un tiempo ($\Delta s$) y el radio ($r$) por la variación del angulo ($\Delta\theta$),

y luego dividimos eso por el tiempo transcurrido ($\Delta t$), obtenemos la relación que nos permite calcular la velocidad ($v$) a lo largo de la órbita, conocida como velocidad tangencial, que es igual a la velocidad angular ($\omega$):

$v_1 = r \omega_1$

$v = r \omega$

Condiciones

Variables

$r$

Radio

$m$

9894

$v$

$v_1$

Velocidad primera etapa

$m/s$

10238

$\omega$

$\omega_1$

Velocidad ángular primera etapa

$rad/s$

10303

Relación

Desarrollo

Como la velocidad media ($\bar{v}$) es con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$), igual a

$\bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$

y con la distancia recorrida en un tiempo ($\Delta s$) expresado como arco de un círculo, y el radio ($r$) y la variación del angulo ($\Delta\theta$) son

$\Delta s=r \Delta\theta$

y la definición de la velocidad angular media ($\bar{\omega}$) es

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

entonces,

$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$

Como la relación es general, se puede aplicar para valores instantáneos, lo que resulta en

$v = r \omega$

.

ID:(3233, 1)

Ecuación

>Top, >Modelo

Si dividimos la relación entre la distancia recorrida en un tiempo ($\Delta s$) y el radio ($r$) por la variación del angulo ($\Delta\theta$),

y luego dividimos eso por el tiempo transcurrido ($\Delta t$), obtenemos la relación que nos permite calcular la velocidad ($v$) a lo largo de la órbita, conocida como velocidad tangencial, que es igual a la velocidad angular ($\omega$):

$v_2 = r \omega_2$

$v = r \omega$

Condiciones

Variables

$r$

Radio

$m$

9894

$v$

$v_2$

Velocidad segunda etapa

$m/s$

10239

$\omega$

$\omega_2$

Velocidad angular segunda etapa

$rad/s$

10304

Relación

Desarrollo

Como la velocidad media ($\bar{v}$) es con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$), igual a

$\bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$

y con la distancia recorrida en un tiempo ($\Delta s$) expresado como arco de un círculo, y el radio ($r$) y la variación del angulo ($\Delta\theta$) son

$\Delta s=r \Delta\theta$

y la definición de la velocidad angular media ($\bar{\omega}$) es

$\bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$

entonces,

$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$

Como la relación es general, se puede aplicar para valores instantáneos, lo que resulta en

$v = r \omega$

.

ID:(3233, 2)