Intercepter à vitesse angulaire constante
Storyboard 
Les objets peuvent s'intersecter lorsqu'ils coïncident en angle au même moment. Pour y parvenir, ils doivent se déplacer à partir de leurs angles de départ respectifs avec des vitesses angulaires leur permettant de coïncider en angle et en temps à la fin du trajet.
ID:(1450, 0)
Intercepter à vitesse angulaire constante
Description 
Les objets peuvent s'intersecter lorsqu'ils coïncident en angle au même moment. Pour y parvenir, ils doivent se déplacer à partir de leurs angles de départ respectifs avec des vitesses angulaires leur permettant de coïncider en angle et en temps à la fin du trajet.
Variables
Calculs
Calculs
Équations
Dans le cas o a vitesse angulaire initiale ($\omega_0$) est gal a vitesse angulaire moyenne ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Par cons quent, avec a différence d'angles ($\Delta\theta$), qui est gal le angle ($\theta$) divis par le angle de départ ($\theta_0$), nous obtenons :
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Et avec le temps écoulé ($\Delta t$), qui est gal le temps ($t$) divis par le temps initial ($t_0$), nous obtenons :
| $ \Delta t \equiv t - t_0 $ |
Nous pouvons r crire l' quation pour a vitesse angulaire moyenne ($\bar{\omega}$) comme suit :
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Cela peut tre exprim comme suit :
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
En r solvant cela, nous obtenons :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Dans le cas o a vitesse angulaire initiale ($\omega_0$) est gal a vitesse angulaire moyenne ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Par cons quent, avec a différence d'angles ($\Delta\theta$), qui est gal le angle ($\theta$) divis par le angle de départ ($\theta_0$), nous obtenons :
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Et avec le temps écoulé ($\Delta t$), qui est gal le temps ($t$) divis par le temps initial ($t_0$), nous obtenons :
| $ \Delta t \equiv t - t_0 $ |
Nous pouvons r crire l' quation pour a vitesse angulaire moyenne ($\bar{\omega}$) comme suit :
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Cela peut tre exprim comme suit :
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
En r solvant cela, nous obtenons :
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Comme a vitesse moyenne ($\bar{v}$) est avec a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$), gal
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
et avec a distance parcourue en un temps ($\Delta s$) exprim comme un arc de cercle, et le radio ($r$) et a variation d'angle ($\Delta\theta$) sont
| $ \Delta s=r \Delta\theta $ |
et la d finition de a vitesse angulaire moyenne ($\bar{\omega}$) est
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
alors,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Comme la relation est g n rale, elle peut tre appliqu e pour des valeurs instantan es, ce qui donne
| $ v = r \omega $ |
(ID 3233)
Comme a vitesse moyenne ($\bar{v}$) est avec a distance parcourue en un temps ($\Delta s$) et le temps écoulé ($\Delta t$), gal
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
et avec a distance parcourue en un temps ($\Delta s$) exprim comme un arc de cercle, et le radio ($r$) et a variation d'angle ($\Delta\theta$) sont
| $ \Delta s=r \Delta\theta $ |
et la d finition de a vitesse angulaire moyenne ($\bar{\omega}$) est
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
alors,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Comme la relation est g n rale, elle peut tre appliqu e pour des valeurs instantan es, ce qui donne
| $ v = r \omega $ |
(ID 3233)
La d finition de a vitesse angulaire moyenne ($\bar{\omega}$) est consid r e comme a variation d'angle ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
et le temps écoulé ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
La relation entre les deux est d finie comme a vitesse angulaire moyenne ($\bar{\omega}$) :
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
La d finition de a vitesse angulaire moyenne ($\bar{\omega}$) est consid r e comme a variation d'angle ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
et le temps écoulé ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
La relation entre les deux est d finie comme a vitesse angulaire moyenne ($\bar{\omega}$) :
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Exemples
(ID 15411)
Dans le cas d'une intersection, il s'agit de deux corps se d pla ant de telle mani re qu'ils se rencontreront en ERROR:10307,0 au moment un temps d'intersection ($t$).
Pour y parvenir, chaque corps :
• Commence son d placement en le heure initiale du premier objet ($t_1$) Le angle initial du premier corps ($\theta_1$) avec une vitesse angulaire du corps 1 ($\omega_1$).
• Commence son d placement en le temps initial du deuxième objet ($t_2$) Le angle initial du deuxième corps ($\theta_2$) avec une vitesse angulaire du corps 2 ($\omega_2$).
Ces conditions doivent tre remplies pour atteindre l'intersection.
Ainsi, les diagrammes angle-temps peuvent tre superpos s comme indiqu dans la repr sentation suivante :
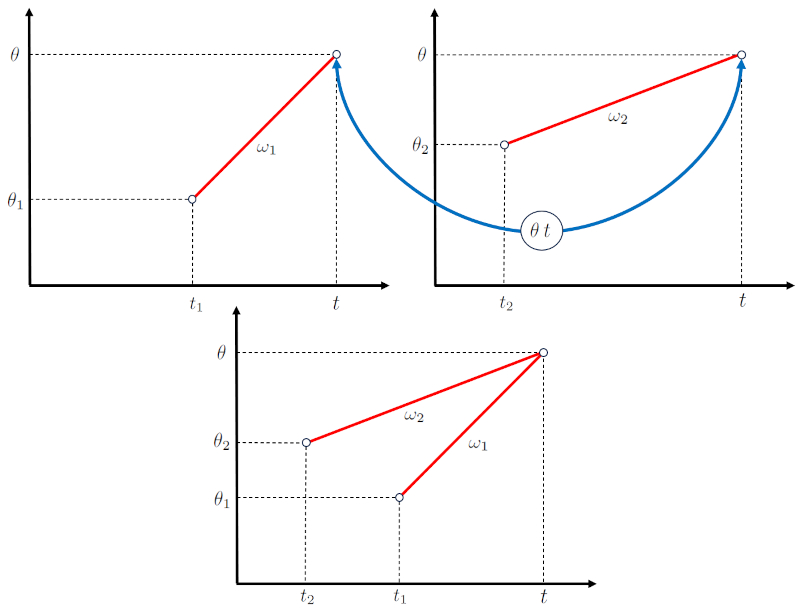
(ID 15517)
Dans le cas d'une intersection ou d'une collision entre deux objets, il est courant que a vitesse angulaire du corps 1 ($\omega_1$) et a vitesse angulaire du corps 2 ($\omega_2$) doivent tre configur s de mani re co ncider.
Cela signifie que le angle parcouru par le premier corps ($\Delta\theta_1$) et a temps de trajet du premier objet ($\Delta t_1$) doivent aboutir une vitesse angulaire du corps 1 ($\omega_1$),
de sorte qu'avec le angle parcouru par le deuxième corps ($\Delta\theta_2$) et a temps de trajet du deuxième objet ($\Delta t_2$), nous obtenons une vitesse angulaire du corps 2 ($\omega_2$),
pour qu'ils co ncident finalement en temps et en espace (position) :
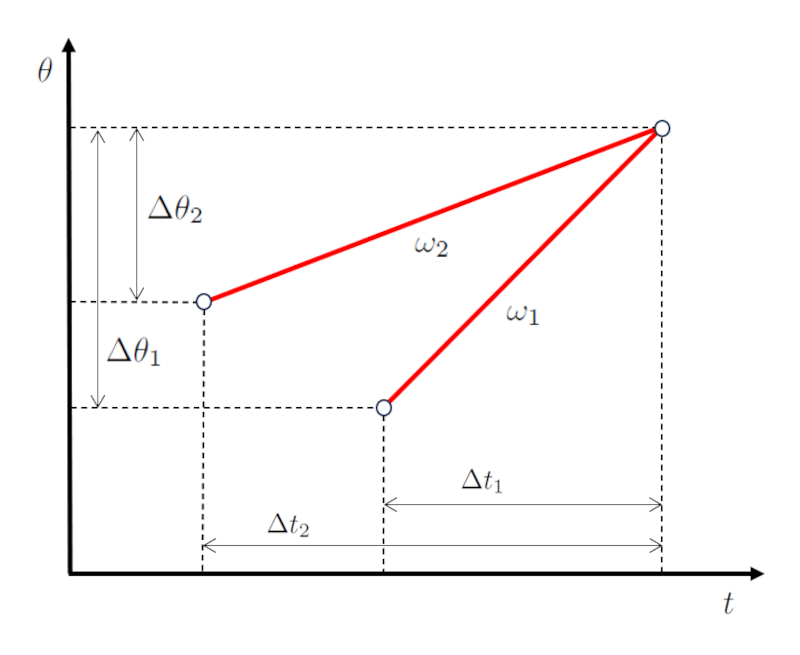
(ID 15516)
Dans le cas d'un mouvement o deux objets s'interceptent, tels que a angle d'intersection ($\theta$) et le temps d'intersection ($t$), cela est commun chacun d'eux. Ainsi, si pour le premier objet le heure initiale du premier objet ($t_1$) et le angle initial du premier corps ($\theta_1$) avec a vitesse angulaire du corps 1 ($\omega_1$) sont respect s :
| $ \theta = \theta_1 + \omega_1 ( t - t_1 )$ |
et pour le deuxi me objet le temps initial du deuxième objet ($t_2$) et le angle initial du deuxième corps ($\theta_2$) avec a vitesse angulaire du corps 2 ($\omega_2$) sont respect s :
| $ \theta = \theta_2 + \omega_2 ( t - t_2 )$ |
ce qui est repr sent comme suit :

(ID 15518)
(ID 15422)
ID:(1450, 0)
