Mit konstanter Winkelgeschwindigkeit abfangen
Storyboard 
Objekte können sich schneiden, wenn sie im gleichen Moment im Winkel übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Anfangswinkeln mit Winkelgeschwindigkeiten bewegen, die es ihnen ermöglichen, sich am Ende der Reise im Winkel und zur gleichen Zeit zu treffen.
ID:(1450, 0)
Mit konstanter Winkelgeschwindigkeit abfangen
Beschreibung 
Objekte können sich schneiden, wenn sie im gleichen Moment im Winkel übereinstimmen. Um dies zu erreichen, müssen sie sich von ihren jeweiligen Anfangswinkeln mit Winkelgeschwindigkeiten bewegen, die es ihnen ermöglichen, sich am Ende der Reise im Winkel und zur gleichen Zeit zu treffen.
Variablen
Berechnungen
Berechnungen
Gleichungen
Im Fall, dass die Anfängliche Winkelgeschwindigkeit ($\omega_0$) gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist,
| $ \bar{\omega} = \omega_0 $ |
Deshalb erhalten wir mit die Differenz von Winkel ($\Delta\theta$), welches gleich der Winkel ($\theta$) geteilt durch der Anfangswinkel ($\theta_0$) ist:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Und mit der Abgelaufene Zeit ($\Delta t$), welches gleich der Zeit ($t$) geteilt durch der Startzeit ($t_0$) ist:
| $ \Delta t \equiv t - t_0 $ |
Wir k nnen die Gleichung f r die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) umschreiben als:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Dies kann ausgedr ckt werden als:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Bei der L sung erhalten wir:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Im Fall, dass die Anfängliche Winkelgeschwindigkeit ($\omega_0$) gleich die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist,
| $ \bar{\omega} = \omega_0 $ |
Deshalb erhalten wir mit die Differenz von Winkel ($\Delta\theta$), welches gleich der Winkel ($\theta$) geteilt durch der Anfangswinkel ($\theta_0$) ist:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Und mit der Abgelaufene Zeit ($\Delta t$), welches gleich der Zeit ($t$) geteilt durch der Startzeit ($t_0$) ist:
| $ \Delta t \equiv t - t_0 $ |
Wir k nnen die Gleichung f r die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) umschreiben als:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Dies kann ausgedr ckt werden als:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Bei der L sung erhalten wir:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Da die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) gleich ist, was ist
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als Bogen eines Kreises und der Radius ($r$) und die Winkelvariation ($\Delta\theta$) ist
| $ \Delta s=r \Delta\theta $ |
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie f r momentane Werte angewendet werden, was zu
| $ v = r \omega $ |
f hrt.
(ID 3233)
Da die Mittlere Geschwindigkeit ($\bar{v}$) mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) und der Abgelaufene Zeit ($\Delta t$) gleich ist, was ist
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$) als Bogen eines Kreises und der Radius ($r$) und die Winkelvariation ($\Delta\theta$) ist
| $ \Delta s=r \Delta\theta $ |
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) ist
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie f r momentane Werte angewendet werden, was zu
| $ v = r \omega $ |
f hrt.
(ID 3233)
Die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) wird als die Winkelvariation ($\Delta\theta$) betrachtet,
| $ \Delta\theta = \theta_2 - \theta_1 $ |
und der Abgelaufene Zeit ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) definiert:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) wird als die Winkelvariation ($\Delta\theta$) betrachtet,
| $ \Delta\theta = \theta_2 - \theta_1 $ |
und der Abgelaufene Zeit ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
Die Beziehung zwischen beiden wird als die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$) definiert:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Beispiele
(ID 15411)
Im Falle einer Kreuzung bewegen sich zwei K rper so, dass sie sich zur Zeit ein Kreuzungszeit ($t$) an ERROR:10307,0 treffen werden.
Um dies zu erreichen, beginnt jeder K rper:
• Seine Verschiebung bei der Anfangszeit des ersten Objekts ($t_1$) bei der Anfangswinkel des ersten Körpers ($\theta_1$) mit eine Winkelgeschwindigkeit des Körpers 1 ($\omega_1$).
• Seine Verschiebung bei der Anfangszeit des zweiten Objekts ($t_2$) bei der Anfangswinkel des zweiten Körpers ($\theta_2$) mit eine Winkelgeschwindigkeit des Körpers 2 ($\omega_2$).
Diese Bedingungen m ssen erf llt sein, um die Kreuzung zu erreichen.
Die Winkel-Zeit-Diagramme k nnen dann wie folgt berlagert werden:
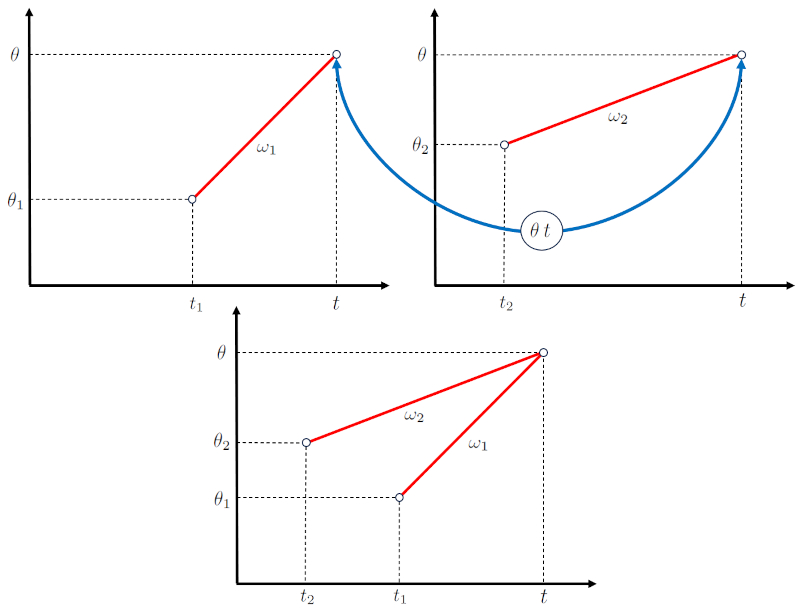
(ID 15517)
Im Falle einer Kreuzung oder Kollision zwischen zwei Objekten ist es blich, dass die Winkelgeschwindigkeit des Körpers 1 ($\omega_1$) und die Winkelgeschwindigkeit des Körpers 2 ($\omega_2$) so konfiguriert sind, dass sie zusammenfallen.
Das bedeutet, dass der Vom ersten Körper zurückgelegter Winkel ($\Delta\theta_1$) und die Reisezeit des ersten Objekts ($\Delta t_1$) zu eine Winkelgeschwindigkeit des Körpers 1 ($\omega_1$) f hren m ssen,
| $ \omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$ |
so dass mit der Vom zweiten Körper zurückgelegter Winkel ($\Delta\theta_2$) und die Reisezeit des zweiten Objekts ($\Delta t_2$) Eine Winkelgeschwindigkeit des Körpers 2 ($\omega_2$) erreicht wird,
| $ \omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$ |
damit sie schlie lich in Zeit und Raum (Position) bereinstimmen:
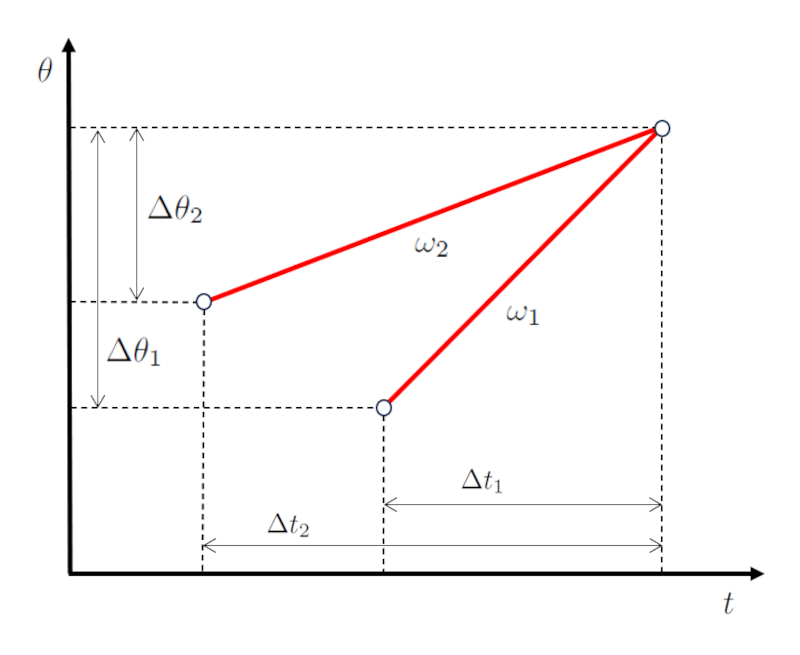
(ID 15516)
Im Fall einer Bewegung, bei der sich zwei Objekte schneiden, wie zum Beispiel die Kreuzungswinkel ($\theta$) und der Kreuzungszeit ($t$), ist dies f r beide blich. Daher, wenn f r das erste Objekt der Anfangszeit des ersten Objekts ($t_1$) und der Anfangswinkel des ersten Körpers ($\theta_1$) mit die Winkelgeschwindigkeit des Körpers 1 ($\omega_1$) erf llt sind:
| $ \theta = \theta_1 + \omega_1 ( t - t_1 )$ |
und f r das zweite Objekt der Anfangszeit des zweiten Objekts ($t_2$) und der Anfangswinkel des zweiten Körpers ($\theta_2$) mit die Winkelgeschwindigkeit des Körpers 2 ($\omega_2$) erf llt sind:
| $ \theta = \theta_2 + \omega_2 ( t - t_2 )$ |
was wie folgt dargestellt wird:

(ID 15518)
(ID 15422)
ID:(1450, 0)
