Oscillators in phase space
Storyboard 
There are different types of oscillators, with the most studied being the spring oscillator and the pendulum. Both are fundamental for understanding key aspects of human movement, such as walking.
On one hand, muscles can behave similarly to a spring, storing and releasing elastic energy during movement. On the other hand, when we walk, certain systems in the bodysuch as the armsact as compensatory oscillators, swinging at the same frequency as our steps to maintain balance and optimize movement dynamics.
In the case of the pendulum, two types are distinguished: the mathematical pendulum, which models the oscillation of a point mass suspended from a massless string, and the physical pendulum, which takes into account the distribution of mass and the geometry of the real object.
ID:(51, 0)
Representación de la Elipse
Definition 
En el espacio de fase la oscilación se puede representar por una elipse
\\n \\nque en forma matemática se escribe como\\n\\n
$\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1$
\\n\\nde semiejes
$x=a\cos u$
\\n\\ny\\n\\n
$y=b\sin u$
ID:(7105, 0)
Oscillators in phase space
Storyboard 
There are different types of oscillators, the most discussed being closed by a spring and the pendulum. Both are relevant to study how we walk. On the one hand there is the behavior similar to a spring that the muscles are capable of showing. On the other hand, when moving, there are systems such as arms that perform compensatory work oscillating with the same frequency of our steps. In the case of the pendulum there are two types, the mathematician who considers the oscillation of a point mass and the physicist who considers the shape of the object as such.
Variables
Calculations
Calculations
Equations
Examples
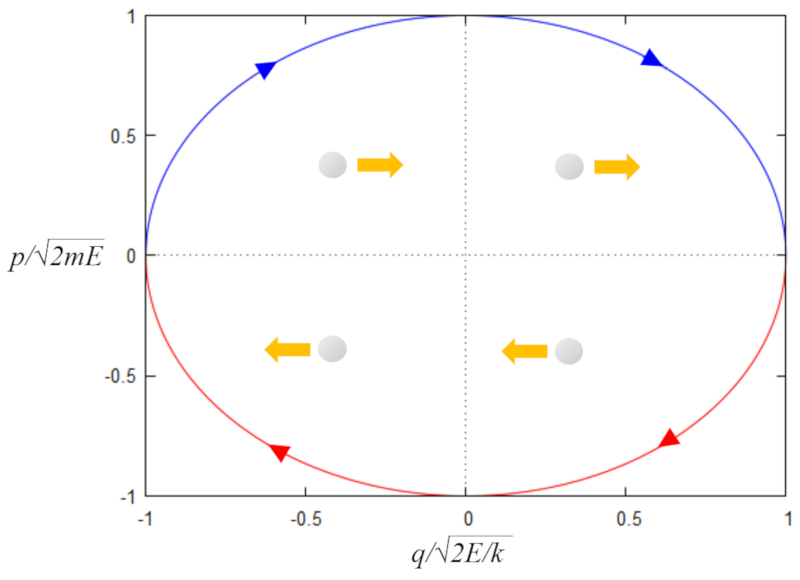
In phase space, the oscillation is represented by an ellipse:
Its general mathematical expression is:
$\displaystyle\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
where the parameters $a$ and $b$ correspond to the major and minor semi-axes, respectively.
This trajectory can also be described parametrically using a parameter $u$, which varies from $0$ to $2\pi$, with the following trigonometric functions:
$x = a \cos u$
and
$y = b \sin u$
In the case of a spring, the total energy the energía del resorte ($E$), which is conserved, is composed of the initial work ($W_0$), associated with the inertial Mass ($m_i$) and the speed ($v$):
The the potential Energy ($V$) of the spring is related to the hooke Constant ($k$) and the position ($x$):
Thus, the total energy the energía del resorte ($E$) is expressed as:
$E_k=\displaystyle\frac{1}{2}m_iv^2+\displaystyle\frac{1}{2}kx^2$
If this expression is rewritten as:
it becomes clear that it corresponds to an ellipse in the velocity the speed ($v$) and elongation the position ($x$) space, whose semiaxes are:
$a=\sqrt{\displaystyle\frac{2E_k}{k}}=x_0$
, and
$b=\sqrt{\displaystyle\frac{2E_k}{m_i}}=v_0$
.
The semiaxes correspond, respectively, to the maximum amplitude
In the case of amplitude, which corresponds to our coordinate the position ($x$), the semiaxis depends on the energía del resorte ($E$) and the hooke Constant ($k$):
$a=\sqrt{\displaystyle\frac{2E_k}{k}}$
Additionally, the time ($t$) is scaled with the period ($T$):
$u=\displaystyle\frac{2\pi t}{T}$
Therefore, the amplitude is expressed as:
In the case of the amplitude, which corresponds to our coordinate the speed ($v$), the semiaxis depends on the energía del resorte ($E$) and the inertial Mass ($m_i$):
$b=\sqrt{\displaystyle\frac{2E}{m}}$
Likewise, the time ($t$) is scaled with the period ($T$):
$u=\displaystyle\frac{2\pi t}{T}$
Therefore, the amplitude is expressed as:
Given that the angular frequency ($\omega$), together with the period ($T$), is equal to:
and that the sound frequency ($\nu$) is equal to:
it follows that:
Since the oscillation obeys physical laws, it is possible to use the fact that the area under the curve the speed ($v$) versus the time ($t$) corresponds to the distance traveled, which allows determining the period. As the speed ($v$) depends on the energía del resorte ($E$), the inertial Mass ($m_i$), and the period ($T$):
$\displaystyle\int_0^{T/2}v(t)dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\int_0^{T/2}\cos \displaystyle\frac{2\pi t}{T}dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\frac{T}{\pi}$
The distance between a minimum and a maximum of the elongation that is, between times
$x_{max}-x_{min}=2\sqrt{\displaystyle\frac{2E}{k}}$
Therefore, it follows that:
With the energía del resorte ($E$), the inertial Mass ($m_i$) and the hooke Constant ($k$), it is possible to define an ellipse in the the position ($x$) The velocidad del resorte ($v$) plane as follows:
The position ($x$) is determined from the energía del resorte ($E$), the hooke Constant ($k$), and the period ($T$), as a function of the time ($t$):
The speed ($v$) is determined from the energía del resorte ($E$), the inertial Mass ($m_i$), and the period ($T$), as a function of the time ($t$):
The period ($T$) is determined from the inertial Mass ($m_i$) and the hooke Constant ($k$) by means of:
The sound frequency ($\nu$) corresponds to the number of times an oscillation occurs within one second. The period ($T$) represents the time it takes for one oscillation to occur. Therefore, the number of oscillations per second is:
Frequency is indicated in Hertz (Hz).
The relationship between the angular frequency ($\omega$) and the sound frequency ($\nu$) is expressed as:
The product of the hooke Constant ($k$) and the inertial Mass ($m_i$) is called the frecuencia angular del resorte ($\omega$) and is defined as:
ID:(51, 0)
