Oszillatoren im Phasenraum
Storyboard 
Es gibt verschiedene Arten von Oszillatoren, wobei der Federoszillator und das Pendel zu den am häufigsten untersuchten gehören. Beide sind entscheidend, um zentrale Aspekte der menschlichen Bewegung, wie das Gehen, zu verstehen.
Einerseits können Muskeln ähnlich wie eine Feder funktionieren, indem sie während der Bewegung elastische Energie speichern und freisetzen. Andererseits wirken bestimmte Körpersysteme, wie beispielsweise die Arme, beim Gehen als kompensatorische Oszillatoren. Sie schwingen mit der gleichen Frequenz wie unsere Schritte, um das Gleichgewicht zu halten und die Bewegungsdynamik zu optimieren.
Beim Pendel unterscheidet man zwei Typen: das mathematische Pendel, das die Schwingung einer punktförmigen Masse an einem masselosen Faden beschreibt, und das physikalische Pendel, das die Massenverteilung und die Geometrie des realen Körpers berücksichtigt.
ID:(51, 0)
Representación de la Elipse
Definition 
En el espacio de fase la oscilación se puede representar por una elipse
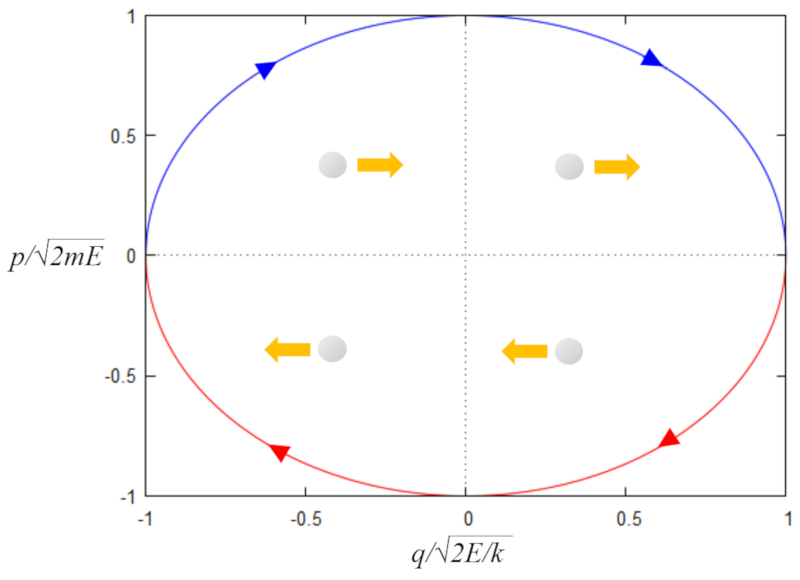
\\n \\nque en forma matemática se escribe como\\n\\n
$\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1$
\\n\\nde semiejes
$x=a\cos u$
\\n\\ny\\n\\n
$y=b\sin u$
ID:(7105, 0)
Oszillatoren im Phasenraum
Beschreibung 
Es gibt verschiedene Arten von Oszillatoren, wobei die meist diskutierten durch eine Feder und das Pendel geschlossen werden. Beide sind relevant, um zu untersuchen, wie wir gehen. Einerseits gibt es das Verhalten einer Feder, das die Muskeln zeigen können. Andererseits gibt es beim Bewegen Systeme wie Arme, die Ausgleichsarbeit leisten und mit der gleichen Frequenz unserer Schritte oszillieren. Beim Pendel gibt es zwei Arten: den Mathematiker, der die Schwingung einer Punktmasse betrachtet, und den Physiker, der die Form des Objekts als solche betrachtet.
Variablen
Berechnungen
Berechnungen
Gleichungen
(ID 12338)
Beispiele
(ID 16244)
Im Phasenraum wird die Schwingung durch eine Ellipse dargestellt:

Ihre allgemeine mathematische Darstellung lautet:
$\displaystyle\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
wobei die Parameter $a$ und $b$ den großen und kleinen Halbachsen entsprechen.
Diese Trajektorie kann auch parametrisch beschrieben werden, mit einem Parameter $u$, der von $0$ bis $2\pi$ variiert, und den folgenden trigonometrischen Funktionen:
$x = a \cos u$
und
$y = b \sin u$
(ID 7105)
Im Fall einer Feder besteht die gesamte Energie die Energía del resorte ($E$), die erhalten bleibt, aus der Anfängliche Arbeit ($W_0$), verbunden mit die Träge Masse ($m_i$) und die Geschwindigkeit ($v$):
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
Die die Potenzielle Energie ($V$) der Feder hängt mit die Hookes Konstante ($k$) und die Position ($x$) zusammen:
| $ V =\displaystyle\frac{1}{2} k x ^2$ |
Daraus ergibt sich, dass die Gesamtenergie die Energía del resorte ($E$) geschrieben wird als:
$E_k=\displaystyle\frac{1}{2}m_iv^2+\displaystyle\frac{1}{2}kx^2$
Wenn man diesen Ausdruck umformuliert als:
| $\displaystyle\frac{ v ^2}{\displaystyle\frac{2 E }{ m_i }}+\displaystyle\frac{ x ^2}{\displaystyle\frac{2 E }{ k }}=1$ |
wird deutlich, dass er einer Ellipse im Geschwindigkeits-Die Geschwindigkeit ($v$) und Auslenkungsraum die Position ($x$) entspricht, deren Halbachsen sind:
$a=\sqrt{\displaystyle\frac{2E_k}{k}}=x_0$
, und
$b=\sqrt{\displaystyle\frac{2E_k}{m_i}}=v_0$
.
Die Halbachsen entsprechen jeweils der maximalen Amplitude
(ID 16238)
Im Fall der Amplitude, die unserer Koordinate die Position ($x$) entspricht, hängt die Halbachse von die Energía del resorte ($E$) und die Hookes Konstante ($k$) ab:
$a=\sqrt{\displaystyle\frac{2E_k}{k}}$
Außerdem wird der Zeit ($t$) mit die Zeit ($T$) skaliert:
$u=\displaystyle\frac{2\pi t}{T}$
Daher wird die Amplitude dargestellt durch:
| $ x =\sqrt{\displaystyle\frac{2 E }{ k }}\cos \displaystyle\frac{2 \pi t }{ T }$ |
(ID 16239)
Im Fall der Amplitude, die unserer Koordinate die Geschwindigkeit ($v$) entspricht, hängt die Halbachse von die Energía del resorte ($E$) und die Träge Masse ($m_i$) ab:
$b=\sqrt{\displaystyle\frac{2E}{m}}$
Ebenso wird der Zeit ($t$) mit die Zeit ($T$) skaliert:
$u=\displaystyle\frac{2\pi t}{T}$
Daher wird die Amplitude dargestellt als:
| $ v =-\sqrt{\displaystyle\frac{2 E }{ m_i }}\sin \displaystyle\frac{2 \pi t }{ T }$ |
(ID 16240)
Da die Winkelfrequenz ($\omega$) zusammen mit die Zeit ($T$) gleich ist:
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
und die Frequenz des Schalls ($\nu$) gleich ist:
| $ \nu =\displaystyle\frac{1}{ T }$ |
ergibt sich daraus:
| $ \omega = 2 \pi \nu $ |
(ID 16242)
Da die Schwingung den physikalischen Gesetzen gehorcht, kann man die Tatsache nutzen, dass die Fläche unter der Kurve die Geschwindigkeit ($v$) gegen der Zeit ($t$) dem zurückgelegten Weg entspricht, um die Periode zu bestimmen. Da die Geschwindigkeit ($v$) von die Energía del resorte ($E$), die Träge Masse ($m_i$) und die Zeit ($T$) abhängt:
$\displaystyle\int_0^{T/2}v(t)dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\int_0^{T/2}\cos \displaystyle\frac{2\pi t}{T}dt=\sqrt{\displaystyle\frac{2E}{m}}\displaystyle\frac{T}{\pi}$
Der Weg zwischen einem Minimum und einem Maximum der Auslenkung also zwischen den Zeitpunkten
$x_{max}-x_{min}=2\sqrt{\displaystyle\frac{2E}{k}}$
Daraus ergibt sich:
| $ T =2 \pi \sqrt{\displaystyle\frac{ m_i }{ k }}$ |
(ID 16241)
(ID 16243)
Mit die Energía del resorte ($E$), die Träge Masse ($m_i$) und die Hookes Konstante ($k$) lässt sich eine Ellipse im die Position ($x$)Die Velocidad del resorte ($v$)-Diagramm definieren durch:
| $\displaystyle\frac{ v ^2}{\displaystyle\frac{2 E }{ m_i }}+\displaystyle\frac{ x ^2}{\displaystyle\frac{2 E }{ k }}=1$ |
(ID 7101)
Die Position ($x$) wird aus die Energía del resorte ($E$), die Hookes Konstante ($k$) und die Zeit ($T$) bestimmt, als Funktion von der Zeit ($t$):
| $ x =\sqrt{\displaystyle\frac{2 E }{ k }}\cos \displaystyle\frac{2 \pi t }{ T }$ |
(ID 7102)
Die Geschwindigkeit ($v$) wird aus die Energía del resorte ($E$), die Träge Masse ($m_i$) und die Zeit ($T$) bestimmt, als Funktion von der Zeit ($t$):
| $ v =-\sqrt{\displaystyle\frac{2 E }{ m_i }}\sin \displaystyle\frac{2 \pi t }{ T }$ |
(ID 7104)
Die Zeit ($T$) wird aus die Träge Masse ($m_i$) und die Hookes Konstante ($k$) bestimmt mittels:
| $ T =2 \pi \sqrt{\displaystyle\frac{ m_i }{ k }}$ |
(ID 7106)
Die Frequenz des Schalls ($\nu$) entspricht der Anzahl der Schwingungen, die innerhalb einer Sekunde auftreten. Die Zeit ($T$) repr sentiert die Zeit, die f r eine einzelne Schwingung ben tigt wird. Daher ist die Anzahl der Schwingungen pro Sekunde:
| $ \nu =\displaystyle\frac{1}{ T }$ |
Die Frequenz wird in Hertz (Hz) angegeben.
(ID 4427)
Die Beziehung zwischen die Winkelfrequenz ($\omega$) und die Frequenz des Schalls ($\nu$) wird ausgedrückt als:
| $ \omega = 2 \pi \nu $ |
(ID 12338)
Das Produkt von die Hookes Konstante ($k$) und die Träge Masse ($m_i$) wird als die Frecuencia angular del resorte ($\omega$) bezeichnet und wie folgt definiert:
| $ \omega_0 ^2=\displaystyle\frac{ k }{ m_i }$ |
(ID 1242)
ID:(51, 0)
