Storyboard

Cuando los elementos hidráulicos se conectan en serie, el flujo permanece constante, pero en cada elemento hidráulico se produce una caída de presión. La suma de estas caídas de presión es igual a la caída total, y, por lo tanto, la resistencia hidráulica total es igual a la suma de todas las resistencias hidráulicas individuales. Por otro lado, el inverso de la conductividad hidráulica total es igual a la suma de los inversos de las conductividades hidráulicas.

>Modelo

ID:(1466, 0)

Concepto

>Top

En el caso de una suma en la que los elementos están conectados en serie, la resistencia hidráulica total del sistema se calcula sumando las resistencias individuales de cada elemento.

Dado que los elementos están conectados en serie, la caída de presión ocurre en cada uno de los elementos, mientras que el flujo es constante. Por lo tanto, la diferencia de presión total ($\Delta p_t$) será igual a la suma de la diferencia de presión en una red ($\Delta p_k$). Cada uno de estos elementos, de acuerdo con la ley de Darcy, es igual a la resistencia hidráulica en una red ($R_{hk}$) multiplicado por el flujo de volumen en una red ($J_{Vk}$):

$\Delta p_k = R_{hk} J_{Vk}$

Así que la suma de la resistencia hidráulica en una red ($R_{hk}$) será igual a la resistencia hidráulica total en serie ($R_{st}$).

ID:(3630, 0)

Ecuación

>Top, >Modelo

Si observamos la ley de Hagen-Poiseuille que nos permite calcular el flujo de volumen ($J_V$) a partir de el radio del cilindro ($R$), la viscosidad ($\eta$), el largo de tubo ($\Delta L$) y la diferencia de presión ($\Delta p$):

podemos identificar parámetros relacionados con la geometría (el largo de tubo ($\Delta L$) y el radio del cilindro ($R$)) y el tipo de líquido (la viscosidad ($\eta$)), que pueden denominarse conjuntamente como una conductancia hidráulica ($G_h$):

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

Condiciones

Variables

$G_h$

Conductancia hidráulica

$m^4/kg s$

$\Delta L$

Largo de tubo

$m$

$\pi$

Pi

3.1415927

$rad$

$R$

Radio del cilindro

$m$

$\eta$

Viscosidad

$Pa s$

Relación

ID:(15102, 0)

Ecuación

>Top, >Modelo

Con la introducción de la conductancia hidráulica ($G_h$), podemos reformular la ecuación de Hagen-Poiseuille con la diferencia de presión ($\Delta p$) y el flujo de volumen ($J_V$) a través de la siguiente ecuación:

$ J_V = G_h \Delta p $

Condiciones

Variables

$G_h$

Conductancia hidráulica

$m^4/kg s$

$\Delta p$

Diferencia de presión

$Pa$

$J_V$

Flujo de volumen

$m^3/s$

Relación

Desarrollo

Si observamos la ley de Hagen-Poiseuille, que nos permite calcular el flujo de volumen ($J_V$) a partir de el radio del cilindro ($R$), la viscosidad ($\eta$), el largo de tubo ($\Delta L$) y la diferencia de presión ($\Delta p$):

$ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$

podemos introducir la conductancia hidráulica ($G_h$) definido en términos de el largo de tubo ($\Delta L$), el radio del cilindro ($R$) y la viscosidad ($\eta$) de la siguiente manera:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

y así obtener:

$ J_V = G_h \Delta p $

ID:(14471, 0)

Ecuación

>Top, >Modelo

En el contexto de la resistencia eléctrica, existe su inverso, conocido como la conductancia eléctrica. De manera análoga, se puede definir lo que sería la conductancia hidráulica ($G_h$) en función de la resistencia hidráulica ($R_h$) mediante la expresión:

$ R_h = \displaystyle\frac{1}{G_h }$

Condiciones

Variables

$G_h$

Conductancia hidráulica

$m^4/kg s$

$R_h$

Resistencia hidráulica

$kg/m^4s$

Relación

ID:(15092, 0)

Ecuación

>Top, >Modelo

Dado que la resistencia hidráulica ($R_h$) es igual al inverso de la conductancia hidráulica ($G_h$), podemos calcularlo a partir de la expresión de este último. De esta manera, podemos identificar parámetros relacionados con la geometría (el largo de tubo ($\Delta L$) y el radio del cilindro ($R$)) y el tipo de líquido (la viscosidad ($\eta$)), que pueden ser denominados colectivamente como una resistencia hidráulica ($R_h$):

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

Condiciones

Variables

$\Delta L$

Largo de tubo

$m$

$\pi$

Pi

3.1415927

$rad$

$R$

Radio del cilindro

$m$

$R_h$

Resistencia hidráulica

$kg/m^4s$

$\eta$

Viscosidad

$Pa s$

Relación

Desarrollo

Dado que la resistencia hidráulica ($R_h$) es igual a la conductancia hidráulica ($G_h$) según la siguiente ecuación:

$ R_h = \displaystyle\frac{1}{G_h }$

y dado que la conductancia hidráulica ($G_h$) se expresa en términos de la viscosidad ($\eta$), el radio del cilindro ($R$) y el largo de tubo ($\Delta L$) de la siguiente manera:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$

podemos concluir que:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

ID:(3629, 0)

Ecuación

>Top, >Modelo

Como el flujo de volumen ($J_V$) se puede calcular a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) mediante la siguiente ecuación:

puede despejarse en términos de la diferencia de presión ($\Delta p$), teniendo en cuenta que el inverso de la resistencia hidráulica ($R_h$) es la conductancia hidráulica ($G_h$), lo que nos lleva a la siguiente expresión:

$ \Delta p = R_h J_V $

Condiciones

Variables

$\Delta p$

Diferencial de la presión

$Pa$

$J_V$

Flujo de volumen

$m^3/s$

$R_h$

Resistencia hidráulica

$kg/m^4s$

Relación

Desarrollo

El flujo de volumen ($J_V$) se puede calcular a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) mediante la siguiente ecuación:

$ J_V = G_h \Delta p $

Por otro lado con lado con la relación para la resistencia hidráulica ($R_h$)

$ R_h = \displaystyle\frac{1}{G_h }$

por lo que se obtiene

$ \Delta p = R_h J_V $

que Henry Darcy formuló para modelar el comportamiento general de medios porosos más complejos por los cuales fluye un líquido.

La genialidad de esta forma de reescribir la ley de Hagen-Poiseuille es que muestra la analogía que existe entre el flujo de corriente eléctrica y el flujo de líquido. En este sentido, la ley de Hagen-Poiseuille corresponde a la ley de Ohm. Esto abre la posibilidad de aplicar los conceptos de redes eléctricas a sistemas de tuberías por donde fluye un líquido.

Esta ley, también conocida como Ley de Darcy-Weisbach, fue publicada por primera vez en la obra de Darcy:

• "Les fontaines publiques de la ville de Dijon" ("Las Fuentes Públicas de la Ciudad de Dijon"), Henry Darcy, Victor Dalmont Editeur, París (1856).

ID:(3179, 0)

Ecuación

>Top, >Modelo

La diferencia de presión total ($\Delta p_t$) en relación a las distintas diferencia de presión en una red ($\Delta p_k$), lo que nos lleva a la siguiente conclusión:

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $

Condiciones

Variables

$\Delta p_k$

Caída de presión en cada capa

$Pa$

$\Delta p_t$

Diferencia de presión total en capas en paralelo

$Pa$

Relación

ID:(4377, 0)

Ecuación

>Top, >Modelo

En el caso de una resistencia hidráulica en una red ($R_{hk}$), su valor se calcula utilizando la viscosidad ($\eta$), el radio del cilindro ($R$) y el largo de tubo ($\Delta L$) a través de la siguiente ecuación:

Cuando hay varias resistencias hidráulicas conectadas en serie, podemos calcular la resistencia hidráulica total en serie ($R_{st}$) sumando la resistencia hidráulica en una red ($R_{hk}$), como se expresa en la siguiente fórmula:

$ R_{st} =\displaystyle\sum_k R_{hk} $

Condiciones

Variables

$R_h$

Resistencia hidráulica

$kg/m^4s$

$R_{ss}$

Resistencia hidráulica en una red

$kg/m^4s$

Relación

Desarrollo

Una forma de modelar un tubo en el que varía la sección es dividirlo en secciones de radio constante y luego sumar las resistencias hidráulicas en serie. Supongamos que tenemos una serie de la resistencia hidráulica en una red ($R_{hk}$), que depende de la viscosidad ($\eta$), el radio del cilindro ($R$) y el largo de tubo ($\Delta L$) a través de la siguiente ecuación:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

En cada elemento habrá Una diferencia de presión en una red ($\Delta p_k$) con la resistencia hidráulica en una red ($R_{hk}$) y el flujo de volumen ($J_V$) para los que se aplica la ley de Darcy

$ \Delta p = R_h J_V $

la diferencia de presión total ($\Delta p_t$) será igual a la suma de las diferencia de presión en una red ($\Delta p_k$) individuales

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $

por lo que

$\Delta p=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$

Por lo tanto, el sistema se puede modelar como un conducto único con la resistencia hidráulica calculada como la suma de las componentes individuales:

$ R_{st} =\displaystyle\sum_k R_{hk} $

ID:(3180, 0)

Concepto

>Top

En el caso de una suma en la que los elementos están conectados en serie, la conductancia hidráulica total del sistema se calcula sumando las conductancias individuales de cada elemento.

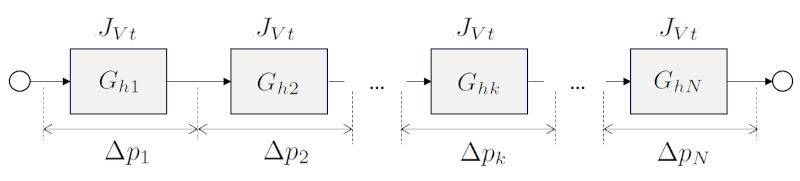
Dado que los elementos están conectados en serie, la caída de presión ocurre en cada uno de los elementos, mientras que el flujo es constante. Por lo tanto, la diferencia de presión total ($\Delta p_t$) será igual a la suma de la diferencia de presión en una red ($\Delta p_k$). Cada uno de estos elementos, de acuerdo con la ley de Darcy, es igual a el flujo de volumen en una red ($J_{Vk}$) dividido por la conductancia hidráulica en una red ($G_{hk}$):

$\Delta p_k = \displaystyle\frac{J_{Vk}}{K_{hk}}$

Así que la suma del inverso de la conductancia hidráulica en una red ($G_{hk}$) será igual al inverso de la conductancia hidráulica total en serie ($K_{st}$).

ID:(11067, 0)

Ecuación

>Top, >Modelo

En el caso de la suma de elementos en serie, la resistencia hidráulica total en serie ($R_{st}$) es igual a la suma de la resistencia hidráulica en una red ($R_{hk}$):

Dado que la resistencia hidráulica en una red ($R_{hk}$) es el inverso de la conductancia hidráulica en una red ($G_{hk}$), obtenemos:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

Condiciones

Variables

$R_{h1}$

Resistencia hidráulica 1

$kg/m^4s$

$R_{h2}$

Resistencia hidráulica 2

$kg/m^4s$

$R_{pt}$

Resistencia hidráulica total en paralelo

$kg/m^4s$

Relación

Desarrollo

La resistencia hidráulica total en serie ($R_{st}$), junto con la resistencia hidráulica en una red ($R_{hk}$) en

$ R_{st} =\displaystyle\sum_k R_{hk} $

y junto con la conductancia hidráulica en una red ($G_{hk}$) y la ecuación

$ R_h = \displaystyle\frac{1}{G_h }$

conduce a

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

ID:(3633, 0)

Descripción

>Top

Con el caso de 3 resistencias hidráulicas y empleando la ley de Darcy

y la suma de las presiones

y la suma serial de las resistencias hidráulicas

se pueden calcular las caídas de presión en base a las resistencias hidrodinámicas y la presión total

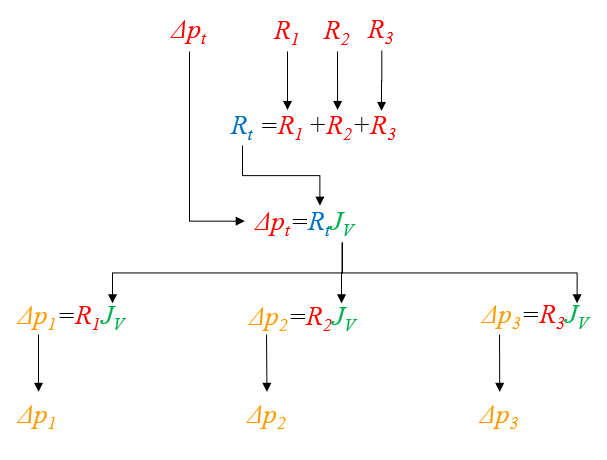
ID:(11069, 0)