Usuario:
Presión sonora
Storyboard 
El movimiento de las moléculas del medio generan variaciones en la densidad y presión en el medio lo que se puede detectar.
ID:(1589, 0)
Presión sonora
Storyboard
El movimiento de las moléculas del medio generan variaciones en la densidad y presión en el medio lo que se puede detectar.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
La variaci n del momento $dp$ est asociada a la masa de las mol culas $m$ y a la velocidad del sonido $u$ de las mol culas mediante:
$dp = 2mu \approx mu$
As , en un intervalo de tiempo igual al periodo $dt \approx T$, tenemos:
$F=\displaystyle\frac{dp}{dt}=\displaystyle\frac{mu}{T}$
Por lo tanto, la presión sonora ($p_s$) se puede calcular utilizando la presi n
la velocidad del sonido ($c$) es
y el volumen con moléculas ($\Delta V$) que var a
de la siguiente manera:
$p=\displaystyle\frac{1}{S} \displaystyle\frac{dp}{dt}=\displaystyle\frac{1}{S}\displaystyle\frac{mu}{T}=\displaystyle\frac{muc}{ScT}=\displaystyle\frac{muc}{S\lambda}=\displaystyle\frac{muc}{\Delta V}=\rho u c$
Donde en el ltimo t rmino, se multiplic el numerador y el denominador por $c$. La expresi n en el denominador es el volumen del gas desplazado por el sonido en $T$, por lo que podemos reemplazar la masa dividida por este volumen por la densidad, quedando:
Como ERROR:5104 calculado a partir de la presión sonora ($p_s$) e la velocidad de la molécula ($u$) usando
junto com a express o para la presión sonora ($p_s$) em termos de la densidad del medio ($\rho$) e la velocidad del sonido ($c$)
obtemos
Ejemplos
Cuando el sonido se propaga, provoca el desplazamiento de las mol culas en el borde del sistema, lo que resulta en impactos contra la pared. Estos impactos transfieren momento a la pared, lo que equivale a una fuerza. Dado que la fuerza es generada por un gran n mero de part culas, su efecto depende de la superficie del sistema, lo que da lugar a una presi n.
Es importante entender que la presi n sonora no es igual a la presi n ambiental. En el aire, esta ltima est del orden de $10^5,Pa$, mientras que la presi n sonora suele ser mucho menor que $1,Pa$.
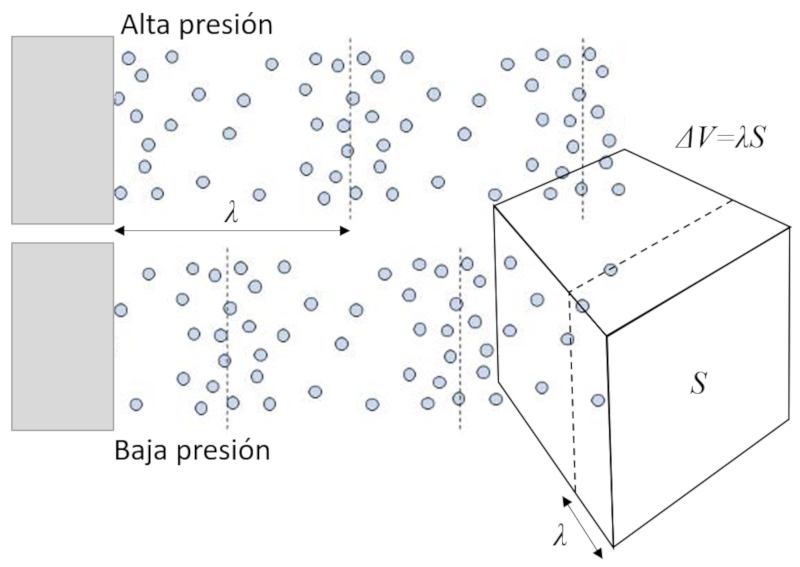
Si desplazamos la cara de un cubo, generaremos un aumento o disminuci n de concentraci n, lo que conlleva una disminuci n o aumento de los choques de las mol culas con la cara del volumen:
Como la presi n es la transferencia de momento por el choque de la mol cula con la pared, la variaci n del volumen lleva a un aumento o disminuci n de la presi n.
La presión de la columna de agua ($p$) se calcula a partir de la fuerza de la columna ($F$) y la sección de la columna ($S$) de la siguiente manera:
Cuando una onda sonora atraviesa un volumen con moléculas ($\Delta V$), este se expande y contrae a lo largo de una distancia del orden de un largo de Onda de Sonido ($\lambda$), lo que resulta en una variaci n de volumen que depende de la sección o superficie ($S$) del volumen perpendicular a la direcci n de propagaci n.
Por lo tanto, la variaci n del volumen es igual a:
La presión sonora ($p_s$) se puede entender como la densidad de momento calculada de la densidad del medio ($\rho$) y la velocidad de la molécula ($u$), la cual se multiplica por la velocidad del sonido ($c$) usando
El nivel de ruido ($L$) abarca un amplio rango de la presión sonora ($p_s$), lo que hace til definir una escala que mitigue esta dificultad. Para ello, podemos trabajar con el logaritmo de la presi n normalizado por un valor que corresponda al cero en esta escala. Si tomamos la presi n m nima que una persona puede detectar y que definimos como la presión de referencia ($p_{ref}$), podemos definir una escala mediante:
que comienza en 0 para el rango audible. En el caso del aire, la presión de referencia ($p_{ref}$) es de $20 \mu Pa$.
El concepto de ERROR:5104,0 proporciona una medida de la resistencia del sistema para transmitir la onda sonora. Se considera una presi n que act a y se establece una medida en la que el medio expuesto es desplazado. De esta manera, se compara la presión sonora ($p_s$) con la velocidad de la molécula ($u$).
Por lo tanto, ERROR:5104 se define como:
Para calcular ERROR:5104 a partir de la densidad del medio ($\rho$) y la velocidad del sonido ($c$), se utiliza la f rmula:
ID:(1589, 0)
