User:
Sound pressure
Storyboard
The movement of the molecules of the medium generate variations in the density and pressure in the medium, which can be detected.
ID:(1589, 0)
Sound Pressure
Description
As sound propagates, it causes displacement of molecules at the boundary of the system, leading to impacts against the wall. These impacts transfer momentum to the wall, resulting in a force. Because the force is generated by a high number of particles, its effect depends on the surface area of the system, giving rise to a pressure.
It's important to understand that sound pressure is not the same as ambient pressure. In air, the latter is on the order of $10^5,Pa$, whereas sound pressure is typically much lower than $1,Pa$.
ID:(134, 0)
Formation of pressure
Concept
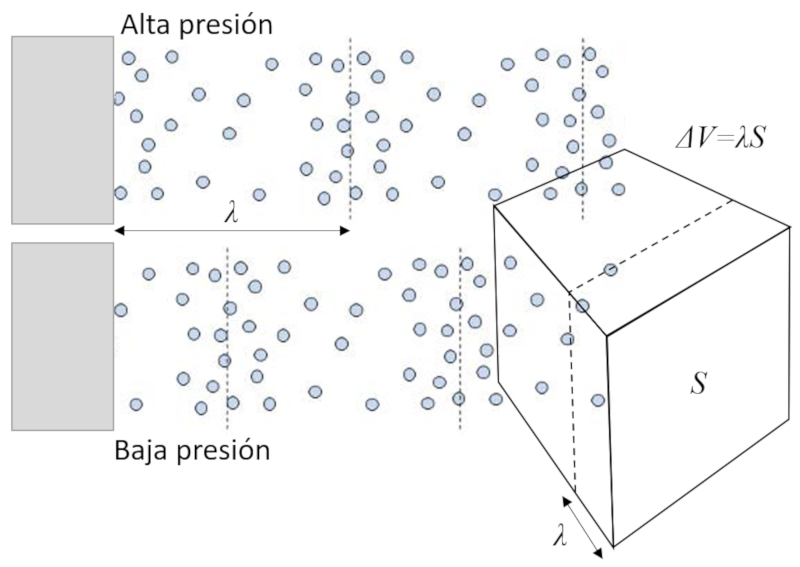
If we displace a cube's face, we generate an increase or decrease in concentration, which leads to a decrease or increase in collisions of molecules with the face of the volume:
Since pressure is the transfer of momentum due to collisions of molecules with the wall, the change in volume leads to an increase or decrease in pressure.
ID:(1865, 0)
Model
Concept
Variables
Parameters
Selected parameter
Calculations
Equation
$ \Delta V = S \lambda $
DV = S * lambda
$ F =\displaystyle\frac{ d p }{ d t }$
F = dp / dt
$ L = 20 \log_{10}\left(\displaystyle\frac{ p }{ p_{ref} }\right)$
L = 20* log10( p / p_ref )
$ p \equiv\displaystyle\frac{ F }{ S }$
p = F / S
$ p = \rho c u $
p = rho * c * u
$ Z =\displaystyle\frac{ p }{ u }$
Z = p / u
$ Z = \rho c $
Z = rho * c
ID:(15453, 0)
Definition of pressure
Equation
To model the motion of liquid elements, it is necessary to move from a point-force and mass view to elements of volume exposed to forces on one of their faces and mass calculated with density.
Therefore, pressure is defined as force per unit area and is calculated using:
 $ p \equiv\displaystyle\frac{ F }{ S }$ |
where P is pressure, F is force, and A is the area on which the force acts. The unit of pressure in the International System of Units is the pascal (Pa), which is defined as one newton per square meter (N/m²). Pressure can vary depending on depth, height of the liquid column, and other factors.
ID:(4342, 0)
Force exerted by molecules
Equation
According to Newton, force can be expressed as the change in momento de la partícula ($p$). This momentum is generated by the rebound of particles, which transfer momentum to the wall. Since momentum is conserved and the particle's momentum changes from $p_{particle}$ to $-p_{particle}$ upon rebound, by momentum conservation we then have:
$p_{particle} = p_{wall} - p_{particle}$
which implies
$p_{wall} = 2p_{particle}$
Thus, the change in the momento de la partícula ($p$) on the wall is the time ($t$), generating force exerted by the Molecules ($F$), which is
| $ F =\displaystyle\frac{ d p }{ d t }$ |
ID:(3390, 0)
Volume with molecules
Equation
When a sound wave travels through ($$), it expands and contracts over a distance on the order of ($$), resulting in a volume variation depending on the section or Area ($S$) perpendicular to the direction of propagation.
Therefore, the volume variation is equal to:
| $ \Delta V = S \lambda $ |
ID:(3398, 0)
Variation of the moment by molecules
Equation
The sound pressure ($p$) can be understood as the momentum density calculated from the mean density ($\rho$) and the molecule speed ($u$), which is then multiplied by the speed of sound ($c$) via
| $ p = \rho c u $ |
The variation in momentum $dp$ is associated with the mass of the molecules $m$ and the velocity of sound $u$ through:
$dp = 2mu \approx mu$
Thus, in a time interval equal to the period $dt \approx T$, we have:
$F=\displaystyle\frac{dp}{dt}=\displaystyle\frac{mu}{T}$
Therefore, the sound pressure ($p$) can be calculated using the pressure
the speed of sound ($c$) is
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
and the volume with molecules ($\Delta V$) which varies
| $ \Delta V = S \lambda $ |
as follows:
$p=\displaystyle\frac{1}{S} \displaystyle\frac{dp}{dt}=\displaystyle\frac{1}{S}\displaystyle\frac{mu}{T}=\displaystyle\frac{muc}{ScT}=\displaystyle\frac{muc}{S\lambda}=\displaystyle\frac{muc}{\Delta V}=\rho u c$
In the last term, both numerator and denominator are multiplied by $c$. The expression in the denominator represents the volume of gas displaced by the sound in $T$, so we can replace the mass divided by this volume with density, yielding:
| $ p = \rho c u $ |
ID:(3391, 0)
Noise level as function of the sound pressure, air
Equation
The noise level, air ($L$) encompasses a wide range of the sound pressure ($p$), making it useful to define a scale that mitigates this difficulty. To do so, we can work with the logarithm of the pressure normalized by a value corresponding to zero on this scale. If we take the minimum pressure that a person can detect, defined as the reference pressure ($p_{ref}$), we can define a scale using:
| $ L = 20 \log_{10}\left(\displaystyle\frac{ p }{ p_{ref} }\right)$ |
which starts at 0 for the audible range. In the case of air, the reference pressure ($p_{ref}$) is $20 \mu Pa$.
ID:(3407, 0)
Acoustic impedance
Equation
The concept of impedance ($Z$) provides a measure of the system's resistance to transmit the sound wave. It considers a pressure acting and establishes a measure in which the exposed medium is displaced. In this way, the sound pressure ($p$) is compared to the molecule speed ($u$).
Therefore, impedance ($Z$) is defined as:
| $ Z =\displaystyle\frac{ p }{ u }$ |
ID:(3414, 0)
Impedance in waves
Equation
To calculate impedance ($Z$) from the mean density ($\rho$) and the speed of sound ($c$), the formula used is:
| $ Z = \rho c $ |
Since impedance ($Z$) is calculated from the sound pressure ($p$) and the molecule speed ($u$) using
| $ Z =\displaystyle\frac{ p }{ u }$ |
along with the expression for the sound pressure ($p$) in terms of the mean density ($\rho$) and the speed of sound ($c$),
| $ p = \rho c u $ |
we obtain
| $ Z = \rho c $ |
ID:(12413, 0)