Druyd:Knowledge

Gaußsche Verteilung

Storyboard

In der Grenze ähnlicher Wahrscheinlichkeiten wird die Binomialverteilung in der kontinuierlichen Grenze zur Gaußschen Verteilung reduziert.

>Modell

ID:(1556, 0)

Beispielvergleich mit der Gaußschen Verteilung

Definition

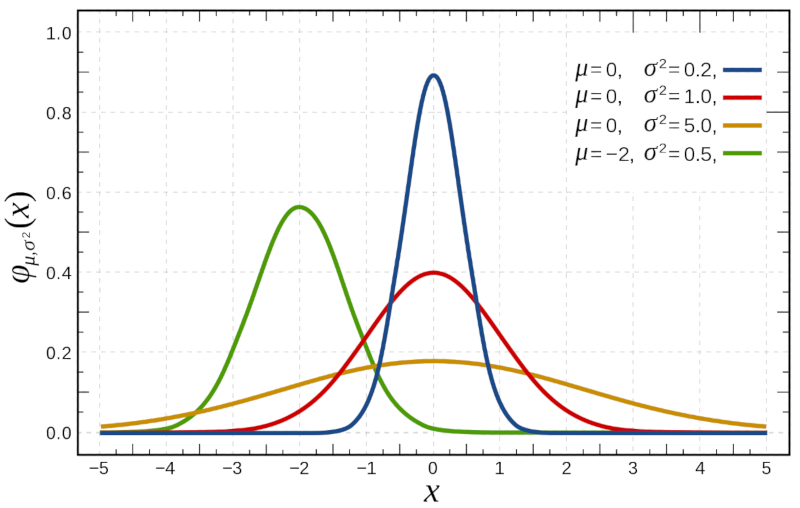
Wenn wir die Binomialverteilung für große Zahlen N und Wahrscheinlichkeiten um 1/2 untersuchen

$P(x)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}$

welches unten dargestellt ist:

ID:(7793, 0)

Gaußsche Verteilung

Storyboard

In der Grenze ähnlicher Wahrscheinlichkeiten wird die Binomialverteilung in der kontinuierlichen Grenze zur Gaußschen Verteilung reduziert.

Variablen

Symbol

Text

Variable

Wert

Einheiten

Berechnen

MKS-Wert

MKS-Einheiten

$\sigma$

sigma

Desviación estándar de Gauss

$q$

Número de pasos hacia la derecha

$n_1$

n_1

Número de pasos hacia la izquierda

$N$

Número total de pasos

$n$

Número totales de pasos a la izquierda

$u$

Parameter $u$

$s$

Posición camino aleatorio

$\mu$

Posición media

$P_N(m)$

P_Nm

Probabilidad de $n_1$ de $N$ pasos hacia la izquierda

$p$

Probabilidad de pasos hacia la izquierda

$a$

Schrittlänge

$n$

Zahl

Berechnungen

Gleichung

Zahl

Zuerst die Gleichung auswählen:

, dann die Variable auswählen:

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable

Gegeben

Berechnen

Ziel :

Gleichung

Zu verwenden

Gleichungen

$W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}p^n(1-p)^{N-n}$

W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}p^n(1-p)^{N-n}

$\displaystyle\frac{N!}{n!(N-n)!}\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}$

\displaystyle\frac{N!}{n!(N-n)!}\sim\displaystyle\frac{1}{\sqrt{2\pi N}}\left(\displaystyle\frac{n}{N}\right)^{-n-1/2}\left(\displaystyle\frac{N-n}{N}\right)^{-N+n-1/2}

$P(x)=\displaystyle\frac{1}{\sqrt{2\pi N^2p(1-p)}}e^{-(x-aNp)^2/2N^2p(1-p)}$

P(x)=1/(sqrt(2 * pi * N ^2 * p * (1 - p ))) exp(-( x - a * N * p )^2/(2* N ^2 * p * (1- p )))

$P(x)=\displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}$

P(x)=1/(sqrt(2 pi sigma^2))e^(-(x-mu)^2/2sigma^2)

$ W_N(n) =\displaystyle\frac{ N !}{ n !( N - n )!} p ^ n (1- p )^{ N - n }$

W_N(n) =math.factorial( N )* p ^ n *(1- p )^( N - n )/(math.factorial( n )*math.factorial( N - n ))

$ \sigma^2 = N ^2 p (1- p )$

sigma ^2 = N ^2 * p *(1- p )

$x=(n-Np)a$

x=(n-Np)a

$W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}p(1-p)}\left(1+\displaystyle\frac{x}{aNp}\right)^{-n-1/2}\left(1-\displaystyle\frac{x}{aN(1-p)}\right)^{-N+n-1/2}$

W_N(n)\sim\displaystyle\frac{1}{\sqrt{2\pi N}p(1-p)}\left(1+\displaystyle\frac{x}{aNp}\right)^{-n-1/2}\left(1-\displaystyle\frac{x}{aN(1-p)}\right)^{-N+n-1/2}

$N!\sim\sqrt{2\pi N}\left(\displaystyle\frac{N}{e}\right)^N$

N!\sim\sqrt{2\pi N}\left(\displaystyle\frac{N}{e}\right)^N

$(N-n)!\sim\sqrt{2\pi(N-n)}\left(\displaystyle\frac{N-n}{e}\right)^{N-n}$

( N - n )!=sqrt(2* pi *( N - n ))*( N - n )/ e )^( N - n )

$n!\sim\sqrt{2\pi n}\left(\displaystyle\frac{n}{e}\right)^n$

n!\sim\sqrt{2\pi n}\left(\displaystyle\frac{n}{e}\right)^n

$\displaystyle\frac{n}{N}=p\left(1+\displaystyle\frac{x}{aNp}\right)$

\displaystyle\frac{n}{N}=p\left(1+\displaystyle\frac{x}{aNp}\right)

$\displaystyle\frac{N-n}{N}=(1-p)\left(1-\displaystyle\frac{x}{aN(1-p)}\right)$

\displaystyle\frac{N-n}{N}=(1-p)\left(1-\displaystyle\frac{x}{aN(1-p)}\right)

$\left(1+\displaystyle\frac{x}{aNp}\right)\sim e^{x/aNp-x^2/2a^2N^2p^2}$

\left(1+\displaystyle\frac{x}{aNp}\right)\sim e^{x/aNp-x^2/2a^2N^2p^2}

$\left(1-\displaystyle\frac{x}{aN(1-p)}\right)\sim e^{-x/aN(1-p)-x^2/2a^2N^2(1-p)^2}$

\left(1-\displaystyle\frac{x}{aN(1-p)}\right)\sim e^{-x/aN(1-p)-x^2/2a^2N^2(1-p)^2}

$\mu=aNp$

\mu=aNp

$u=\displaystyle\frac{x}{aNp}$

u=\displaystyle\frac{x}{aNp}

$u=\displaystyle\frac{x}{aN(1-p)}$

u=\displaystyle\frac{x}{aN(1-p)}

Beispiele

Distribuci n binomial

Con list=8970 la probabilidad de que se de un numero definido de pasos a la derecha e izquierda esta dada por

equation=8970

con list=3358 el n mero total de pasos es

equation=3358

y solo existe la probabilidad de ir a la derecha o a la izquierda, con list=8965 se tiene para las probabilidades que

equation=8965

por lo que con list se tiene la distribuci n binomial

equation

Ansatz f r $N!$

Mit der Stirling-N herung

equation=8966

und die nderung von Variablen

equation=8996

du verstehst das

equation

Ann herung f r $n!$

Mit der Stirling-N herung

equation=8966

und die nderung von Variablen

equation=11431

du verstehst das

equation

Ann herung f r $(N-n)!$

Mit der Stirling-N herung

equation=8966

und die nderung von Variablen

equation=8997

der Ausdruck ist

equation

Factor $N!/N!(N-n)!$ For $N\gg 1$, $n\gg 1$ and $N>n$

Bei mittleren Wahrscheinlichkeiten p \sim q \sim 1/2 ) und gro en Zahlen N kann dies angezeigt werden

equation=8998

equation=9003

und

equation=8999

bekommst

equation

Grenze von gro en Zahlen und mittleren Wahrscheinlichkeiten

Der Ausdruck

equation=8961

wird reduziert um

equation=507

zur Darstellung

equation

Durchschnittliche Position

Wenn insgesamt N Schritte mit einer Wahrscheinlichkeit p in der richtigen Richtung ausgef hrt werden und diese eine L nge a haben, ist die erwartete Endposition

equation

ndern Sie die Variablen durch Versatz von $x=(n-Np)a$

Um die Gau sche Verteilung zu erhalten, ist es notwendig, die Verteilung um ihre Abweichung von ihrer mittleren Position zu entwickeln, die durch gegeben sein kann

equation

Faktor $n/N$ abh ngig vom Weg $x$

Wie der Weg ist

equation=8973

Faktor n/N kann geschrieben werden als

equation

Faktor $N-n/N$ abh ngig vom Weg $x$

Wie der Weg ist

equation=8973

Faktor n/N kann geschrieben werden als

equation

Binomialverteilung als Funktion der Abweichung

Wenn gro e Zahlen und Wahrscheinlichkeiten um 1/2 in die Binomialverteilung f r den Fall eingegeben werden

equation=506

die Ausdr cke

equation=9004

und

equation=9005

Man erh lt eine Verteilung der Form

equation

Variablen nderung $u=x/aNp$

Um den Faktor 1+x/aNp zu entwickeln, k nnen Sie mit der Variablen nderung arbeiten

equation

Faktor $1+x/aNp$ f r $N\gg 1$ und $p\sim 1/2$

Mit der Ann herung

equation=9001

es muss

equation

Variablen nderung $u=x/aN(1-p)$

Um den Faktor 1+x/aN(1-p) zu entwickeln, k nnen Sie mit der Variablen nderung arbeiten

equation

Faktor $1-x/aN(1-p)$ f r $N\gg 1$ und $p\sim 1/2$

Mit der Ann herung

equation=9001

es muss

equation

Wahrscheinlichkeit f r gro e $N$ und mittlere $p$

Es kann gezeigt werden, dass f r eine gro e Anzahl N und eine Wahrscheinlichkeit p, die weder zu klein noch zu nahe bei 1 liegt, die Binomialverteilung f r die Position auf einen Gau schen Wert reduziert wird x= na:

equation

In diesem Fall wurde die Wahrscheinlichkeit q durch 1-p ersetzt.

Generalisierung der Grenzwerte f r Big Numbers

$\begin{matrix}

P(x) & = & \displaystyle\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2}\\

\sigma^2 & = & Np(1-p)\\

\end{matrix}

Standardabweichung der Gau schen Verteilung

Die Standardabweichung der Binomialverteilung an der Grenze N gro und p mittel ist

equation

Beispielvergleich mit der Gau schen Verteilung

Wenn wir die Binomialverteilung f r gro e Zahlen N und Wahrscheinlichkeiten um 1/2 untersuchen

equation=3368

welches unten dargestellt ist:

image

>Modell

ID:(1556, 0)