User:


Particle in a box and sphere
Storyboard

When we consider a particle within a volume, whether it's a box or a sphere, we can estimate the probability of finding the particle within a range of positions.

>Model

ID:(433, 0)


Phase space of a particle in a box 1D
Definition

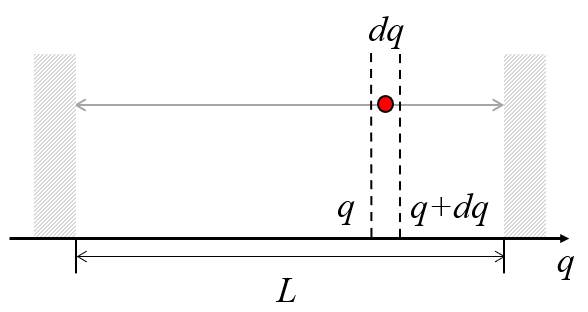
Consider a box of length L in which a particle bounces between both walls traveling with a p moment:

The question is what is the probability of finding it in a dq range.

ID:(11463, 0)


Phase space of a particle in a box 2D
Image

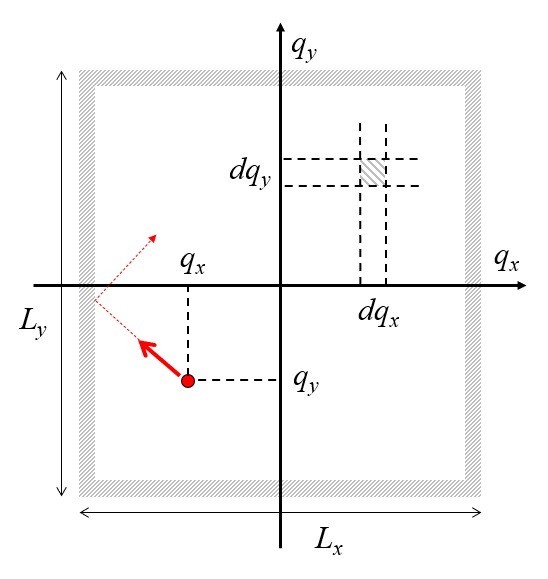
Consider a 2D box of length L_x and width L_y in which a particle bounces between both walls traveling with a (p_x,p_y) moment:

The question is what is the probability of finding it in a quadrilateral of width dq_x and height dq_y.

ID:(11464, 0)


Phase space of a particle in a 3D sphere
Note

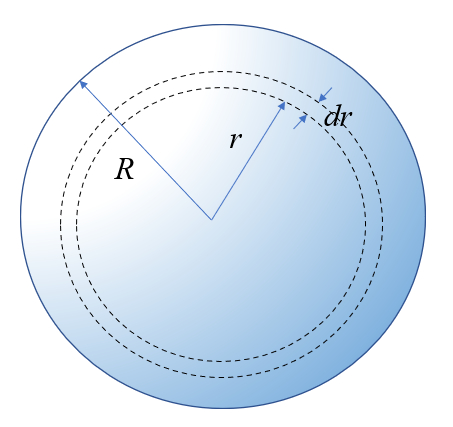
Consider a sphere of radius R in which a particle bounces between both walls traveling with a moment (p_x,p_y,p_z):

The question is what is the probability of finding it in a quadrilateral of width dq_x and height dq_y.

ID:(11465, 0)


Probability of finding the particle in a radius $r$
Quote

La probabilidad de encontrar la partícula en un radio entre r y r+dr es con

$ P(r) = \displaystyle\frac{3 r ^2}{ R ^3 } dr $



que se muestra en la siguiente gráfica:

ID:(11466, 0)


Particle in a box and sphere
Storyboard

When we consider a particle within a volume, whether it's a box or a sphere, we can estimate the probability of finding the particle within a range of positions.

Variables

Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$dq$
dq
Elemento del largo de la caja
m
$dq_x$
dq_x
Elemento del largo de la caja en dirección x
m
$dq_y$
dq_y
Elemento del largo de la caja en dirección y
m
$dr$
dr
Grosor de la capa esférica
m
$L$
L
Largo de la caja
m
$L_x$
L_x
Largo de la caja en dirección x
m
$L_y$
L_y
Largo de la caja en dirección y
m
$P(q_x,q_y)$
P_qxqy
Probabilidad partícula en el rectángulo de rangos en x e y
-
$P_q$
P_q
Probabilidad partícula entre $q$ y $q+dq$
-
$P(r)$
P_r
Probabilidad partícula entre los radios $r$ y $r+dr$
-
$R$
R
Radio de la esfera
m
$r$
r
Radio en que se encuentra la partícula
m

Calculations


First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

Examples

Consider a box of length L in which a particle bounces between both walls traveling with a p moment:

image

The question is what is the probability of finding it in a dq range.

Si se asume que la part cula puede estar en cualquiera posici n en una dimensiones, las posiciones posibles son aquellas descritas por el largo L de la caja.

Las posiciones favorables de encontrar la part cula entre q y q+dq y van a ser con list igual a:

equation

Esto es solo valido si:

Toda posici n es igualmente probable.



lo que se puede generalizar en

Todo estado es igualmente probable.

Adicionalmente se debe notar que la probabilidad esta ntimamente ligada con el rango. Si el rango es nulo, tambi n lo es la probabilidad.

Consider a 2D box of length L_x and width L_y in which a particle bounces between both walls traveling with a (p_x,p_y) moment:

image

The question is what is the probability of finding it in a quadrilateral of width dq_x and height dq_y.

Si se asume que la part cula puede estar en cualquiera posici n en dos dimensiones, las posiciones posibles son aquellas descritas por los largos de las aristas del rect ngulo.

Por ello la probabilidad de encontrar la part cula en el elemento rectangular son con list igual a

equation

Consider a sphere of radius R in which a particle bounces between both walls traveling with a moment (p_x,p_y,p_z):

image

The question is what is the probability of finding it in a quadrilateral of width dq_x and height dq_y.

Si se asume que la part cula puede estar en cualquiera posici n tridimensional dentro de una esfera de radio R, la probabilidad de que se encuentre en una capa con un radio r y r+dr sera igual al volumen de esta:\\n\\n

$4\pi r^2 dr$

\\n\\ndividido por el volumen de la esfera\\n\\n

$\displaystyle\frac{4\pi}{3} R^3$



por lo que con list resulta la probabilidad igual a:

equation

La probabilidad de encontrar la part cula en un radio entre r y r+dr es con list=11474

equation=11474

que se muestra en la siguiente gr fica:

image

>Model

ID:(433, 0)