Utilizador:
Lei de Gauss
Nota 
O fluxo elétrico ($\Phi$) é definida como a componente normal do campo elétrico, calculada a partir de o campo elétrico na superfície i ($\vec{E}_i$) e o versor normal à superfície i ($\hat{n}_i$), multiplicada por la elemento de superfície i ($dS_i$) para cada elemento
i, que é então somada sobre toda a seção:
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
A magnitude de o campo elétrico ($E$) gerada por la charge ($Q$), que estão a uma distância de la distância ($r$), é calculada utilizando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$) da seguinte forma:
| $ E =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2}$ |
Dado que la superfície de uma esfera ($S$) está com la distância ($r$):
| $ S = 4 \pi r ^2$ |
O fluxo é:
$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
A partir disso, podemos inferir que a relação é:
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Usando o elemento de superfície ($dS$) para o produto escalar de o campo elétrico ($\vec{E}$) e o versor normal para seção ($\hat{n}$), obtemos a versão contínua da lei de Gauss:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
Esta corresponde à versão da equação de Gauss descoberta em 1835, que foi publicada postumamente [1].
[1] 'Allgemeine Lehrsätze in Beziehung auf die im verkehrten Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskräfte' (Proposições Gerais Relacionadas às Forças de Atração e Repulsão que Atuam em Proporção ao Inverso do Quadrado da Distância), Carl Friedrich Gauss, Werke, 1867
ID:(15791, 0)
Representação gráfica da lei de Gauss
Citar
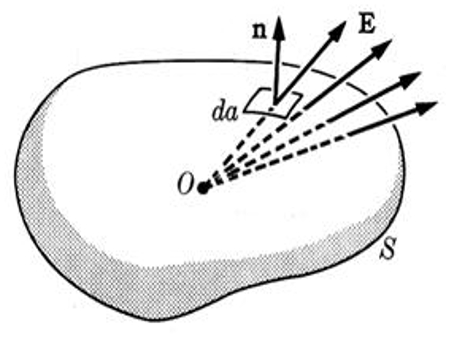
A lei de Gauss considera as linhas de campo em relação a uma superfície fechada.
• Se a superfície não envolve nenhuma carga, as linhas de campo são conservadas, ou seja, fluem tanto para dentro quanto para fora da superfície.
• Se a superfície envolve uma carga la carga total ($Q_t$), um número proporcional a essa carga é criado (carga positiva) ou destruído (carga negativa).
• Se a soma das cargas contidas for nula, a soma das componentes do campo perpendiculares à superfície também será nula.
ID:(224, 0)
Exemplo de campo nulo dentro de um condutor
Exercício
A fuselagem de um avião de passageiros é geralmente um bom condutor de eletricidade. Portanto, se um avião for atingido por um raio, as cargas se distribuem sobre sua superfície e, de acordo com a lei de Gauss, nenhum campo elétrico é gerado dentro da aeronave.
| $ E =0$ |
Dessa forma, os passageiros não são prejudicados e, eventualmente, a carga continua seu caminho, criando um novo raio que se move para outro local carregado positivamente.
Por isso, considera-se que raios não são perigosos para aviões em voo, e cada avião sofre vários impactos por ano. No entanto, existe um risco durante o processo de pouso: se o avião for atingido por um raio no momento em que toca o solo, as cargas podem fluir pelos pneus até a pista, gerando níveis de calor que podem danificá-los. Em geral, os pilotos são treinados para lidar com situações em que o trem de pouso é danificado, de modo que o risco para os passageiros não é muito alto. No entanto, os danos à aeronave podem ser significativos e podem exigir reparos extensos antes que ela possa voltar a operar.
ID:(11374, 0)
Lei de Gauss
Descrição
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
O campo elétrico na superfície i ($\vec{E}_i$) e o versor normal à superfície i ($\hat{n}_i$), multiplicados por la elemento de superfície i ($dS_i$) para cada elemento $i$, que s o ent o somados sobre toda a se o, igual a la carga total ($Q_t$) dividido por la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$):
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Usando o elemento de superfície ($dS$) para o produto escalar de o campo elétrico ($\vec{E}$) e o versor normal para seção ($\hat{n}$), obtemos a vers o cont nua da lei de Gauss:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
(ID 3213)
(ID 3842)
O fluxo elétrico ($\Phi$) definida como a componente normal do campo el trico, calculada a partir de o campo elétrico na superfície i ($\vec{E}_i$) e o versor normal à superfície i ($\hat{n}_i$), multiplicada por la elemento de superfície i ($dS_i$) para cada elemento
i, que ent o somada sobre toda a se o:
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
A magnitude de o campo elétrico ($E$) gerada por la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada utilizando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$) da seguinte forma:
| $ E =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2}$ |
Dado que la superfície de uma esfera ($S$) est com la distância ($r$):
| $ S = 4 \pi r ^2$ |
O fluxo :
$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
A partir disso, podemos inferir que a rela o :
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
(ID 11377)
Exemplos
(ID 15781)
(ID 11375)
O fluxo elétrico ($\Phi$) definida como a componente normal do campo el trico, calculada a partir de o campo elétrico na superfície i ($\vec{E}_i$) e o versor normal à superfície i ($\hat{n}_i$), multiplicada por la elemento de superfície i ($dS_i$) para cada elemento
i, que ent o somada sobre toda a se o:
| $ \Phi \equiv \displaystyle\sum_i \vec{E}_i\cdot\hat{n}_i\,dS_i $ |
A magnitude de o campo elétrico ($E$) gerada por la charge ($Q$), que est o a uma dist ncia de la distância ($r$), calculada utilizando la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$) da seguinte forma:
| $ E =\displaystyle\frac{1}{4 \pi \epsilon_0 \epsilon }\displaystyle\frac{ Q }{ r ^2}$ |
Dado que la superfície de uma esfera ($S$) est com la distância ($r$):
| $ S = 4 \pi r ^2$ |
O fluxo :
$\Phi = | \vec{E} | S = \displaystyle\frac{1}{4 \pi \epsilon \epsilon_0} \displaystyle\frac{ Q }{ r ^2} 4 \pi r ^2=\displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$
A partir disso, podemos inferir que a rela o :
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
Usando o elemento de superfície ($dS$) para o produto escalar de o campo elétrico ($\vec{E}$) e o versor normal para seção ($\hat{n}$), obtemos a vers o cont nua da lei de Gauss:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
Esta corresponde vers o da equa o de Gauss descoberta em 1835, que foi publicada postumamente [1].
[1] 'Allgemeine Lehrs tze in Beziehung auf die im verkehrten Verh ltnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskr fte' (Proposi es Gerais Relacionadas s For as de Atra o e Repuls o que Atuam em Propor o ao Inverso do Quadrado da Dist ncia), Carl Friedrich Gauss, Werke, 1867
(ID 15791)
A lei de Gauss considera as linhas de campo em rela o a uma superf cie fechada.
• Se a superf cie n o envolve nenhuma carga, as linhas de campo s o conservadas, ou seja, fluem tanto para dentro quanto para fora da superf cie.
• Se a superf cie envolve uma carga la carga total ($Q_t$), um n mero proporcional a essa carga criado (carga positiva) ou destru do (carga negativa).
• Se a soma das cargas contidas for nula, a soma das componentes do campo perpendiculares superf cie tamb m ser nula.
(ID 224)
A fuselagem de um avi o de passageiros geralmente um bom condutor de eletricidade. Portanto, se um avi o for atingido por um raio, as cargas se distribuem sobre sua superf cie e, de acordo com a lei de Gauss, nenhum campo el trico gerado dentro da aeronave.
| $ E =0$ |
Dessa forma, os passageiros n o s o prejudicados e, eventualmente, a carga continua seu caminho, criando um novo raio que se move para outro local carregado positivamente.
Por isso, considera-se que raios n o s o perigosos para avi es em voo, e cada avi o sofre v rios impactos por ano. No entanto, existe um risco durante o processo de pouso: se o avi o for atingido por um raio no momento em que toca o solo, as cargas podem fluir pelos pneus at a pista, gerando n veis de calor que podem danific -los. Em geral, os pilotos s o treinados para lidar com situa es em que o trem de pouso danificado, de modo que o risco para os passageiros n o muito alto. No entanto, os danos aeronave podem ser significativos e podem exigir reparos extensos antes que ela possa voltar a operar.
(ID 11374)
(ID 15783)
O fluxo depende de la carga total ($Q_t$) contido no volume. Portanto, devemos somar todas as la carga i ($q_i$) contidas, independentemente de sua posi o:
| $ Q = \displaystyle\sum_ i ^ N q_i$ |
(ID 11376)
O campo elétrico na superfície i ($\vec{E}_i$) e o versor normal à superfície i ($\hat{n}_i$), multiplicados por la elemento de superfície i ($dS_i$) para cada elemento $i$, e depois somados sobre toda a se o, s o iguais a la carga total ($Q_t$) dividido por la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$):
| $ \displaystyle\sum_i \vec{E}_i \cdot \hat{n}_i dS_i = \displaystyle\frac{ Q }{ \epsilon_0 \epsilon }$ |
(ID 11377)
Utilizando o elemento de superfície ($dS$) para o produto escalar de o campo elétrico ($\vec{E}$) e o versor normal para seção ($\hat{n}$), e la carga total ($Q_t$) dividido por la constante de campo elétrico ($\epsilon_0$) e la constante dielétrica ($\epsilon$), chegamos express o da lei de Gauss:
| $\displaystyle\int_S\vec{E}\cdot\hat{n}\,dS=\displaystyle\frac{Q}{\epsilon_0\epsilon}$ |
(ID 3213)
Considere uma carga oca, ou seja, uma esfera oca com cargas na sua superf cie. Nesse caso, podemos definir uma superf cie interna dentro da esfera. Como a quantidade de carga la carga total ($Q_t$) contida no volume zero, o campo el trico o campo elétrico ($E$) tamb m ser zero:
| $ E =0$ |
(ID 3842)
ID:(824, 0)