Sound
Image 
The sound is described as fluctuations in the densities of the particles within the medium through which it propagates. These fluctuations are characteristic of sound, whether it occurs in gases, liquids, or solids.
ID:(515, 0)
Sound generation
Note 
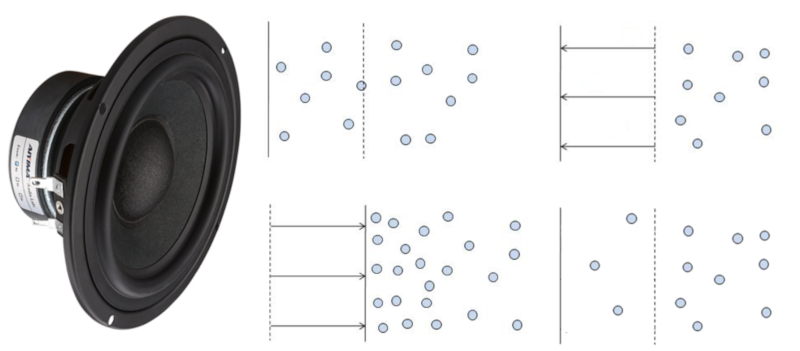
The sound is produced when a surface moves, either increasing or decreasing the volume of gas.
In the first case, the surrounding molecules will occupy the new space, creating a zone of lower air density that will be filled by other neighboring molecules.
In the second case, the surrounding molecules are compressed, resulting in a displacement towards regions of lower density.
Altoparlante
Both changes lead to the propagation of reductions or increases in density, which corresponds to a sound wave.
ID:(1670, 0)
Movement of molecules
Quote 
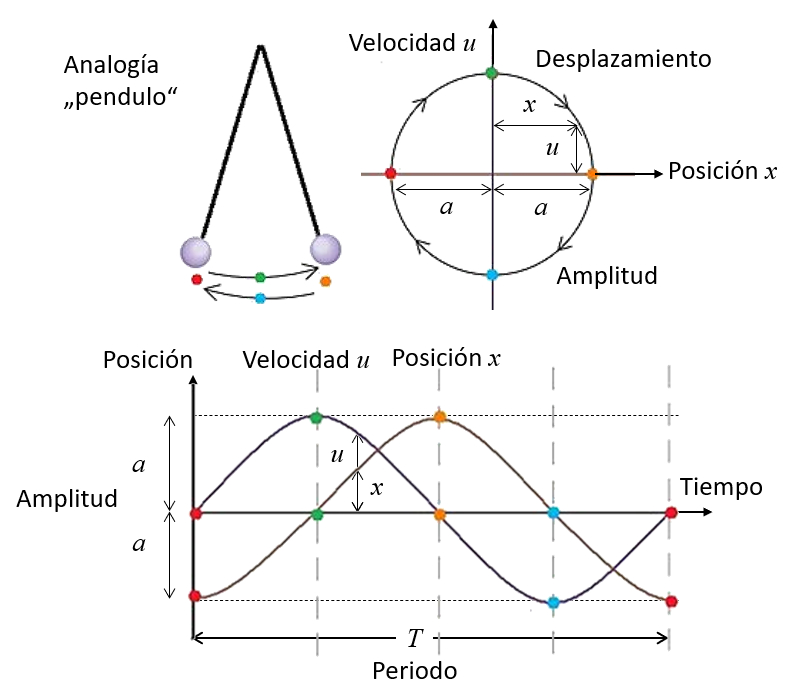
The oscillation of a molecule due to a sound wave can be described in terms of its position and velocity.
If both are plotted as edges on a graph, an elliptical trajectory can be observed. At the vertical extreme points, the particle reaches maximum velocity, with one end being positive (moving from left to right) and the other end being negative (moving from right to left). The horizontal extreme points represent the amplitude, with the left point indicating a minimum value and the right point indicating a positive value.
Similarly, these oscillations can be represented as a function of the time ($t$). If we start from a point where the amplitude Oscillation Molecule ($a$) is initially negative and maximum, the velocity is described by a sine function, while the average Position of the Molecule ($x$) is described by a cosine function that initially has an amplitude negative. However, this choice is arbitrary, since the cycle can start from any other point, for example, when the amplitude is initially zero, as is the case when the sound wave arrives. In the latter case, the position is modeled with a sine function.
ID:(3187, 0)
Propagation of sound
Exercise 
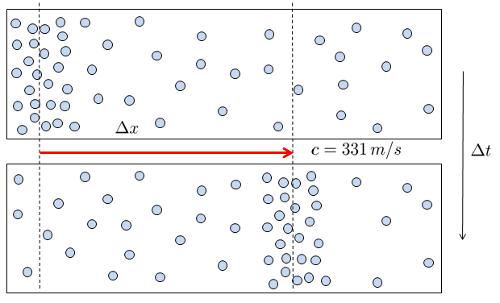
Sound is generated when a surface moves, either increasing or decreasing the volume of a gas.
Once a density/pressure variation is created, it propagates at the wave speed ($c$):
Altoparlante
This is why we are able to hear the sound produced by a speaker.
It is important to recognize:
Sound requires a medium in which density/pressure varies, whether it's gas, liquid, or solid. Therefore, sound cannot propagate in a vacuum.
ID:(11795, 0)
Sound
Storyboard 
Sound consists of fluctuations in the density of a gas, liquid, or solid that can propagate through the medium. Sound exists in all media gas, liquid, or solid with differences in propagation speed and attenuation, although the models that describe it are generally similar.
Variables
Calculations
Calculations
Equations
The speed of sound ($c$) with the wavelength of Sound ($\lambda$) and the period ($T$) is expressed as
and can be rewritten with the sound frequency ($\nu$) as
thus obtaining the relationship
Examples
The sound is described as fluctuations in the densities of the particles within the medium through which it propagates. These fluctuations are characteristic of sound, whether it occurs in gases, liquids, or solids.
The sound is produced when a surface moves, either increasing or decreasing the volume of gas.
In the first case, the surrounding molecules will occupy the new space, creating a zone of lower air density that will be filled by other neighboring molecules.
In the second case, the surrounding molecules are compressed, resulting in a displacement towards regions of lower density.
Both changes lead to the propagation of reductions or increases in density, which corresponds to a sound wave.
The oscillation of a molecule due to a sound wave can be described in terms of its position and velocity.
If both are plotted as edges on a graph, an elliptical trajectory can be observed. At the vertical extreme points, the particle reaches maximum velocity, with one end being positive (moving from left to right) and the other end being negative (moving from right to left). The horizontal extreme points represent the amplitude, with the left point indicating a minimum value and the right point indicating a positive value.
Similarly, these oscillations can be represented as a function of the time ($t$). If we start from a point where the amplitude Oscillation Molecule ($a$) is initially negative and maximum, the velocity is described by a sine function, while the average Position of the Molecule ($x$) is described by a cosine function that initially has an amplitude negative. However, this choice is arbitrary, since the cycle can start from any other point, for example, when the amplitude is initially zero, as is the case when the sound wave arrives. In the latter case, the position is modeled with a sine function.
Sound is generated when a surface moves, either increasing or decreasing the volume of a gas.
Once a density/pressure variation is created, it propagates at the wave speed ($c$):
This is why we are able to hear the sound produced by a speaker.
It is important to recognize:
Sound requires a medium in which density/pressure varies, whether it's gas, liquid, or solid. Therefore, sound cannot propagate in a vacuum.
The average motion generated by the sound wave corresponds to an oscillation around the molecule's original position.
This oscillation can be described using a trigonometric function that involves an amplitude $a$, an angular frequency $\omega$, and time $t$.
The oscillation is described as follows:
The sound frequency ($\nu$) corresponds to the number of times an oscillation occurs within one second. The period ($T$) represents the time it takes for one oscillation to occur. Therefore, the number of oscillations per second is:
Frequency is indicated in Hertz (Hz).
If we consider the velocity versus position diagram, we can interpret oscillation as circular motion in this diagram. In that case, we can estimate ERROR:5715 as the perimeter, which is the distance traveled divided by the elapsed time, which is the period ($T$). If the amplitude Oscillation Molecule ($a$) is the radius, then with the angular frequency ($\omega$):
$u=\displaystyle\frac{2\pi a}{T}=a\omega$
This means that ERROR:5715 is:
The wave speed ($c$) is a velocity, which means it is equal to a length, such as the wavelength ($\lambda$), divided by the time it takes for one oscillation to advance, i.e., the periodo del resorte ($T$). Therefore, we have:
The speed of sound ($c$) is a velocity, which means it is equal to a length, such as the wavelength of Sound ($\lambda$), divided by the time it takes for one oscillation to advance. Since the inverse of time is the sound frequency ($\nu$), we have:
Con
y con
se puede reescribir con
ID:(385, 0)
