Sound pressure
Storyboard 
The movement of the molecules of the medium generate variations in the density and pressure in the medium, which can be detected.
ID:(1589, 0)
Sound Pressure
Image 
As sound propagates, it causes displacement of molecules at the boundary of the system, leading to impacts against the wall. These impacts transfer momentum to the wall, resulting in a force. Because the force is generated by a high number of particles, its effect depends on the surface area of the system, giving rise to a pressure.
It's important to understand that sound pressure is not the same as ambient pressure. In air, the latter is on the order of $10^5,Pa$, whereas sound pressure is typically much lower than $1,Pa$.
ID:(134, 0)
Formation of pressure
Note 
If we displace a cube's face, we generate an increase or decrease in concentration, which leads to a decrease or increase in collisions of molecules with the face of the volume:
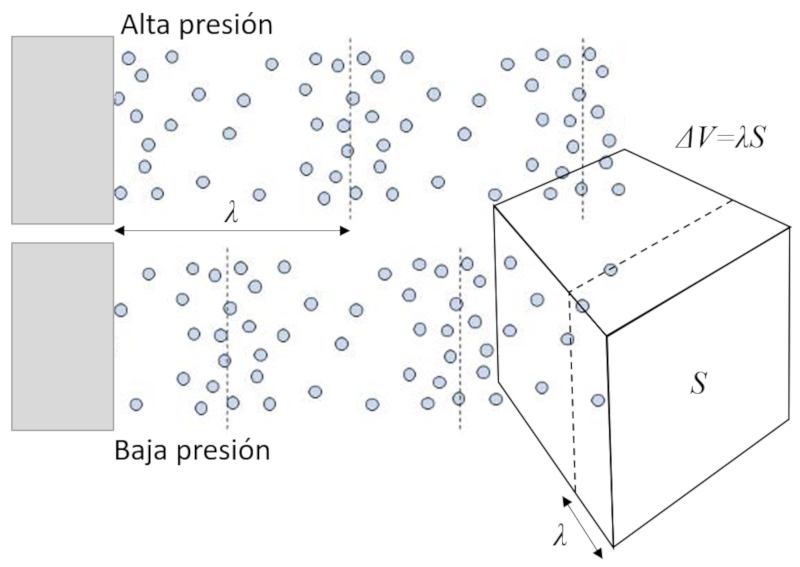
Since pressure is the transfer of momentum due to collisions of molecules with the wall, the change in volume leads to an increase or decrease in pressure.
ID:(1865, 0)
Sound pressure
Storyboard 
The movement of the molecules of the medium generate variations in the density and pressure in the medium, which can be detected.
Variables
Calculations
Calculations
Equations
The variation in momentum $dp$ is associated with the mass of the molecules $m$ and the velocity of sound $u$ through:
$dp = 2mu \approx mu$
Thus, in a time interval equal to the period $dt \approx T$, we have:
$F=\displaystyle\frac{dp}{dt}=\displaystyle\frac{mu}{T}$
Therefore, the sound pressure ($p_s$) can be calculated using the pressure
the speed of sound ($c$) is
and the volume with molecules ($\Delta V$) which varies
as follows:
$p=\displaystyle\frac{1}{S} \displaystyle\frac{dp}{dt}=\displaystyle\frac{1}{S}\displaystyle\frac{mu}{T}=\displaystyle\frac{muc}{ScT}=\displaystyle\frac{muc}{S\lambda}=\displaystyle\frac{muc}{\Delta V}=\rho u c$
In the last term, both numerator and denominator are multiplied by $c$. The expression in the denominator represents the volume of gas displaced by the sound in $T$, so we can replace the mass divided by this volume with density, yielding:
Since ERROR:5104 is calculated from the sound pressure ($p_s$) and the molecule speed ($u$) using
along with the expression for the sound pressure ($p_s$) in terms of the mean density ($\rho$) and the speed of sound ($c$),
we obtain
Examples
As sound propagates, it causes displacement of molecules at the boundary of the system, leading to impacts against the wall. These impacts transfer momentum to the wall, resulting in a force. Because the force is generated by a high number of particles, its effect depends on the surface area of the system, giving rise to a pressure.
It's important to understand that sound pressure is not the same as ambient pressure. In air, the latter is on the order of $10^5,Pa$, whereas sound pressure is typically much lower than $1,Pa$.
If we displace a cube's face, we generate an increase or decrease in concentration, which leads to a decrease or increase in collisions of molecules with the face of the volume:
Since pressure is the transfer of momentum due to collisions of molecules with the wall, the change in volume leads to an increase or decrease in pressure.
The water column pressure ($p$) is calculated from the column force ($F$) and the column Section ($S$) as follows:
When a sound wave travels through ERROR:5080.1, it expands and contracts over a distance on the order of ERROR:5079.1, resulting in a volume variation depending on the section or Area ($S$) perpendicular to the direction of propagation.
Therefore, the volume variation is equal to:
The sound pressure ($p_s$) can be understood as the momentum density calculated from the mean density ($\rho$) and the molecule speed ($u$), which is then multiplied by the speed of sound ($c$) via
The noise level ($L$) encompasses a wide range of the sound pressure ($p_s$), making it useful to define a scale that mitigates this difficulty. To do so, we can work with the logarithm of the pressure normalized by a value corresponding to zero on this scale. If we take the minimum pressure that a person can detect, defined as the reference pressure ($p_{ref}$), we can define a scale using:
which starts at 0 for the audible range. In the case of air, the reference pressure ($p_{ref}$) is $20 \mu Pa$.
The concept of ERROR:5104,0 provides a measure of the system's resistance to transmit the sound wave. It considers a pressure acting and establishes a measure in which the exposed medium is displaced. In this way, the sound pressure ($p_s$) is compared to the molecule speed ($u$).
Therefore, ERROR:5104 is defined as:
To calculate ERROR:5104 from the mean density ($\rho$) and the speed of sound ($c$), the formula used is:
ID:(1589, 0)
