Benützer:
Schalldruck
Storyboard 
Die Bewegung der Moleküle des Mediums erzeugt Schwankungen in der Dichte und im Druck im Medium, die erfasst werden können.
ID:(1589, 0)
Schalldruck
Storyboard
Die Bewegung der Moleküle des Mediums erzeugt Schwankungen in der Dichte und im Druck im Medium, die erfasst werden können.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Die Variation des Impulses $dp$ ist mit der Masse der Molek le $m$ und der Schallgeschwindigkeit $u$ der Molek le verbunden durch:
$dp = 2mu \approx mu$
Daher haben wir in einem Zeitintervall, das dem Periodenintervall $dt \approx T$ entspricht:
$F=\displaystyle\frac{dp}{dt}=\displaystyle\frac{mu}{T}$
Daher kann die Schalldruck ($p_s$) berechnet werden unter Verwendung des Drucks
die Speed of Sound ($c$) ist
und der Volumen mit Molekülen ($\Delta V$), welcher variiert
wie folgt:
$p=\displaystyle\frac{1}{S} \displaystyle\frac{dp}{dt}=\displaystyle\frac{1}{S}\displaystyle\frac{mu}{T}=\displaystyle\frac{muc}{ScT}=\displaystyle\frac{muc}{S\lambda}=\displaystyle\frac{muc}{\Delta V}=\rho u c$
Im letzten Term werden sowohl Z hler als auch Nenner mit $c$ multipliziert. Der Ausdruck im Nenner repr sentiert das Volumen des Gases, das durch den Schall in $T$ verdr ngt wird. Daher k nnen wir die Masse durch dieses Volumen geteilt durch die Dichte ersetzen und erhalten:
Da ERROR:5104 aus die Schalldruck ($p_s$) und die Molecule Geschwindigkeit ($u$) berechnet wird, indem man
zusammen mit dem Ausdruck f r die Schalldruck ($p_s$) in Bezug auf die Mittlere Dichte ($\rho$) und die Speed of Sound ($c$) verwendet,
erhalten wir
Beispiele
Wenn sich der Schall ausbreitet, verursacht er eine Verschiebung von Molek len am Rand des Systems, was zu St en gegen die Wand f hrt. Diese St e bertragen dementsprechend Impuls auf die Wand, was einer Kraft entspricht. Da die Kraft durch eine gro e Anzahl von Partikeln erzeugt wird, h ngt ihre Wirkung von der Oberfl che des Systems ab, was zu einem Druck f hrt.
Es ist wichtig zu verstehen, dass der Schalldruck nicht dem Umgebungsdruck entspricht. In Luft liegt letzterer typischerweise im Bereich von $10^5,Pa$, w hrend der Schalldruck in der Regel weit unter $1,Pa$ liegt.
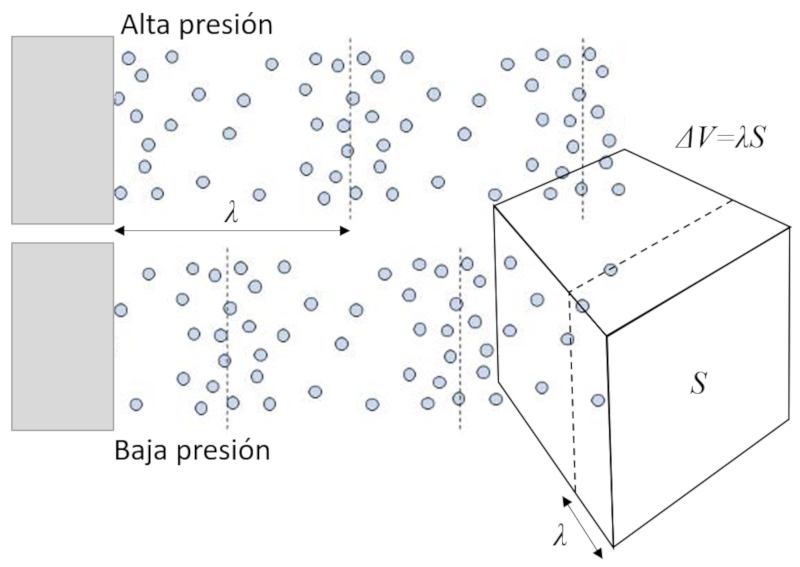
Wenn wir das Gesicht eines W rfels verschieben, erzeugen wir eine Zunahme oder Abnahme der Konzentration, was zu einer Abnahme oder Zunahme der Kollisionen von Molek len mit der Fl che des Volumens f hrt:
Da Druck die bertragung von Impuls durch Kollisionen von Molek len mit der Wand ist, f hrt die Ver nderung des Volumens zu einer Zunahme oder Abnahme des Drucks.
Die Druck der Wassersäule ($p$) wird aus die Kraft der Säule ($F$) und die Column Abschnitt ($S$) wie folgt berechnet:
Wenn eine Schallwelle durch ein Volumen mit Molekülen ($\Delta V$) verl uft, dehnt sie sich aus und zieht sich ber eine Entfernung von ungef hr ein Wellenlänge des Schalles ($\lambda$) zusammen, was zu einer Volumenvariation abh ngig von die Abschnitt oder Bereich ($S$) senkrecht zur Ausbreitungsrichtung f hrt.
Daher ist die Volumenvariation gleich:
Die Schalldruck ($p_s$) kann verstanden werden als die berechnete Impulsdichte von die Mittlere Dichte ($\rho$) und die Molecule Geschwindigkeit ($u$), die dann mit die Speed of Sound ($c$) multipliziert wird durch
Der Geräuschpegel ($L$) umfasst einen weiten Bereich von die Schalldruck ($p_s$), was es sinnvoll macht, eine Skala zu definieren, die diese Schwierigkeit mildert. Daf r k nnen wir mit dem Logarithmus des Drucks arbeiten, der durch einen Wert normalisiert ist, der null auf dieser Skala entspricht. Wenn wir den minimalen Druck nehmen, den eine Person wahrnehmen kann, definiert als die Referenzdruck ($p_{ref}$), k nnen wir eine Skala definieren mittels:
die im h rbaren Bereich bei 0 beginnt. Im Fall von Luft betr gt die Referenzdruck ($p_{ref}$) $20 \mu Pa$.
Das Konzept von ERROR:5104,0 liefert ein Ma f r den Widerstand des Systems, um die Schallwelle zu bertragen. Es ber cksichtigt einen wirkenden Druck und etabliert eine Ma einheit, in der das exponierte Medium verschoben wird. Auf diese Weise wird die Schalldruck ($p_s$) mit die Molecule Geschwindigkeit ($u$) verglichen.
Daher wird ERROR:5104 definiert als:
Um ERROR:5104 aus die Mittlere Dichte ($\rho$) und die Speed of Sound ($c$) zu berechnen, wird die Formel verwendet:
ID:(1589, 0)
