Utilisateur:
Mécanismes
Définition 
Le cycle Diesel est un cycle thermodynamique qui sous-tend le fonctionnement des moteurs diesel, largement utilisés dans les véhicules et les machines industrielles. Développé par Rudolf Diesel dans les années 1890, ce cycle se distingue principalement de celui d'Otto, utilisé dans les moteurs à essence, par son processus d'allumage. Dans le cycle Diesel, l'air est aspiré dans le cylindre et comprimé à un taux beaucoup plus élevé que dans les moteurs à essence, ce qui élève sa température à un niveau suffisant pour enflammer le carburant diesel sans nécessiter de bougie d'allumage.
Lors de son fonctionnement, le cycle commence par l'admission d'air lorsque le piston descend. L'air est ensuite comprimé lors de la remontée du piston, augmentant sa température. Au sommet de la phase de compression, du carburant est injecté dans l'air comprimé et chaud sous forme de fine brume, provoquant une ignition spontanée. La combustion pousse le piston vers le bas, générant ainsi de l'énergie. Enfin, lors de la phase d'échappement, les gaz de combustion sont expulsés lorsque le piston remonte, complétant ainsi le cycle.
Les moteurs Diesel sont reconnus pour leur efficacité et leur durabilité. Le haut taux de compression permet non seulement d'extraire plus d'énergie du carburant, mais augmente également l'efficience thermique, signifiant qu'une plus grande partie de l'énergie du carburant est convertie en travail mécanique. Les moteurs Diesel offrent généralement une meilleure efficacité énergétique et produisent moins d'émissions de CO2 par unité d'énergie que leurs homologues à essence, mais ils peuvent émettre des niveaux plus élevés d'autres polluants, tels que les oxydes d'azote et les particules.
ID:(15283, 0)
Cycle de Carnot
Image
Sadi Carnot a introduit [1] le concept théorique du premier projet de machine capable de générer du travail mécanique basé sur un gradient de température. Cela est réalisé grâce à un processus dans l'espace pression-volume où la chaleur est ajoutée et extraite, comme illustré dans l'image :
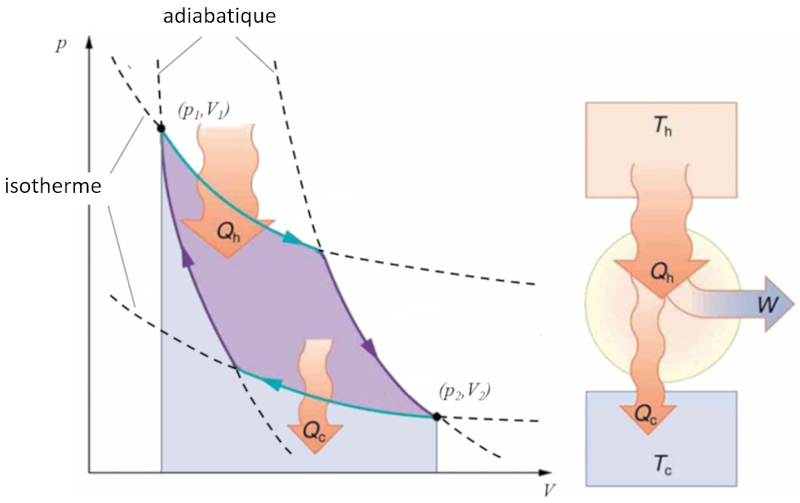
La zone sous la courbe le chaleur fournie ($Q_H$), s'étendant de 1 à 2, représente l'énergie nécessaire pour passer de l'état ($p_1, V_1$) à l'état ($p_2, V_2$). En revanche, la zone sous la courbe le chaleur absorbée ($Q_C$), allant de 2 à 1, représente l'extraction d'énergie nécessaire pour revenir de l'état ($p_2, V_2$) à l'état ($p_1, V_1$). La différence entre ces zones correspond à la région délimitée par les deux courbes et représente le travail efficace ($W$) que le système peut accomplir.
Carnot a également démontré que, conformément au deuxième principe de la thermodynamique, le chaleur fournie ($Q_H$) ne peut pas être nul. Cela implique qu'il n'existe pas de machines capables de convertir toute la chaleur en travail.
[1] "Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance", Sadi Carnot, Annales scientifiques de lÉ.N.S. 2e série, tome 1, p. 393-457 (1872)
ID:(11131, 0)
Cycle diesel : diagramme pression-volume
Noter
Rudolf Diesel [1] s'est lancé dans la création d'un cycle différent du cycle de Carnot dans le but d'atteindre une meilleure efficacité par rapport au cycle de Otto. Ce processus se déroule en plusieurs étapes :
• Étape 1 à 2 : Compression adiabatique $(p_1,V_1,T_1)\rightarrow (p_2,V_2,T_2)$,
• Étape 2 à 3 : Chauffage et expansion à pression constante $(p_2,V_2,T_2)\rightarrow (p_2,V_3,T_3)$,
• Étape 3 à 4 : Expansion adiabatique $(p_2,V_3,T_3)\rightarrow (p_3,V_1,T_4)$,
• Étape 4 à 1 : Refroidissement à volume constant $(p_3,V_1,T_4)\rightarrow (p_1,V_1,T_1)$
Ces étapes sont illustrées ci-dessous :
La clé réside dans l'étape 2 à 3, où l'expansion se produit à pression constante. La raison en devient évidente en examinant le graphique :
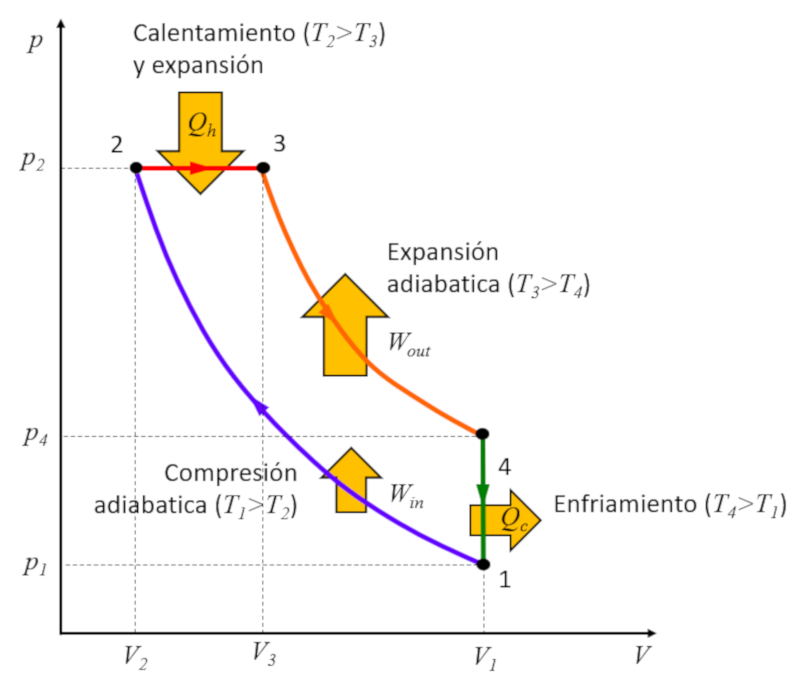
L'énergie gagnée est égale à la surface à l'intérieur du cycle, et en effectuant la compression à pression constante, cette surface est plus grande que dans le cas de la compression à volume constant.
[1] "Verfahren zur Entwickelung eines rationellen Wärmemotors zum Ersatz der Dampfmaschine und der heute bekannten Verbrennungsmotoren" (Méthode pour le Développement d'un Moteur Thermique Rationnel pour Remplacer la Machine à Vapeur et les Moteurs à Combustion Contemporains), Rudolf Diesel, Kaiserlichen Patentamts, No. 67207 (1892)
ID:(11141, 0)
Analyse d'efficacité
Citation
Tant le cycle Otto que le cycle Diesel dépendent des variables a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$). Cependant, dans le cas du cycle Diesel, il dépend également de le indice adiabatique ($\kappa$), dont la valeur est de 1,4.
Dans le cycle Otto, l'efficacité est calculée en fonction de la température à l'aide de l'équation suivante :
| $ \eta =1-\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
Alors que dans le cycle Diesel, l'efficacité est calculée en fonction de la température à l'aide de l'équation suivante :
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
L'inclusion du facteur $1/\kappa \sim 0,71$ dans le cycle Diesel le rend plus efficace par rapport au cycle Otto pour la même configuration de température. Cela résulte directement de l'agrandissement de la zone contenue dans la courbe qui représente le cycle dans la représentation pression-volume.
ID:(11153, 0)
Expansion adiabatique
Exercer
Étant donné qu'en cas d'expansion adiabatique, le gaz satisfait aux relations le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$), et le indice adiabatique ($\kappa$), exprimées comme suit :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Nous pouvons observer que lors du changement d'état de le volume intermédiaire ($V_3$) et a température à l'état 3 ($T_3$) à Le volume étendu ($V_1$) et a température à l'état 4 ($T_4$), l'égalité suivante est vérifiée :
$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$
En utilisant l'équation pour le facteur d'extensibilité ($r_E$) :
| $ r_E =\displaystyle\frac{ V_1 }{ V_3 }$ |
Nous obtenons :
| $ T_3 = T_4 r_E ^{ \kappa - 1}$ |
ID:(15751, 0)
Chaleur fournie
Équation
Étant donné qu'en cas d'expansion adiabatique, le gaz satisfait aux relations le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$) et le indice adiabatique ($\kappa$), exprimées comme suit :
| $ T_i V_i ^{ \kappa -1}= T_f V_f ^{ \kappa -1}$ |
Nous pouvons noter que lors du changement d'état de le volume étendu ($V_1$) et a température à l'état 1 ($T_1$) à Le volume compressé ($V_2$) et a température à l'état 2 ($T_2$), l'égalité suivante est vérifiée :
$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$
En utilisant l'équation pour le entropie molaire de la vapeur ($r_C$) :
| $ r_C =\displaystyle\frac{ V_1 }{ V_2 }$ |
Nous obtenons :
| $ T_2 = T_1 r_C ^{ \kappa - 1}$ |
ID:(15752, 0)
Chauffage au gaz
Script
Comme le réchauffement se produit à pression constante, la loi de Charles s'applique :
| $\displaystyle\frac{ V_i }{ T_i }=\displaystyle\frac{ V_f }{ T_f }$ |
Ainsi, le changement d'état ($V_2, T_2$) à ($V_3, T_3$) doit satisfaire à l'équation :
$\displaystyle\frac{T_2}{V_2} = \displaystyle\frac{T_3}{V_3}$
Avec les équations :
| $ r_C =\displaystyle\frac{ V_1 }{ V_2 }$ |
| $ r_E =\displaystyle\frac{ V_1 }{ V_3 }$ |
nous pouvons réécrire comme suit :
$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$
c'est-à-dire :
| $ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $ |
ID:(15753, 0)
Efficacité en fonction des températures
Variable
L'efficacité en fonction de la température est définie par :
| $ \eta = 1-\displaystyle\frac{ Q_C }{ Q_H } $ |
avec les quantités de chaleur fournies :
| $ Q_H = C_p ( T_3 - T_2 )$ |
et absorbées :
| $ Q_C = C_V ( T_4 - T_1 )$ |
nous avons la relation d'efficacité en fonction de la température :
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
ID:(15754, 0)
Efficacité en fonction des facteurs de compression et d'expansion
Audio
La valeur de a efficacité ($\eta$) peut être calculée à l'aide des valeurs le indice adiabatique ($\kappa$), a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$) dans l'équation suivante :
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ T_4 - T_1 }{ T_3 - T_2 }$ |
De plus, les relations entre les températures avec le entropie molaire de la vapeur ($r_C$) et le facteur d'extensibilité ($r_E$) sont définies par les équations suivantes :
| $ T_2 = T_1 r_C ^{ \kappa - 1}$ |
| $ T_3 = T_4 r_E ^{ \kappa - 1}$ |
| $ T_3 =\displaystyle\frac{ r_C }{ r_E } T_2 $ |
De plus, la valeur de le indice adiabatique ($\kappa$) est utilisée dans l'équation :
| $ \kappa =\displaystyle\frac{ C_p }{ C_V }$ |
Ces équations nous permettent de calculer la performance d'un processus suivant le cycle Diesel à l'aide de l'équation suivante :
| $ \eta =1-\displaystyle\frac{1}{ \kappa }\displaystyle\frac{ r_E ^{- \kappa }- r_C ^{- \kappa }}{ r_E ^{-1}- r_C ^{-1}}$ |
ID:(15755, 0)
Le Cycle Diesel
Storyboard
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
En suivant une analogie avec le ERROR:5219,0 pour les liquides et les solides avec a capacité calorique ($C$) et a masse ($M$) :
il existe galement un chaleur spécifique des gaz à volume constant ($c_V$) pour le chauffage volume constant avec a capacité thermique à volume constant ($C_V$) :
En suivant une analogie avec le ERROR:5219,0 pour les liquides et les solides avec a capacité calorique ($C$) et a masse ($M$) :
il existe galement un chaleur spécifique à pression constante ($c_p$) pour le chauffage pression constante avec a capacité thermique à pression constante ($C_p$) :
Lorsque l'on fournit le chaleur fournie ($Q_H$), la temp rature du gaz augmente de $T_2$ $T_3$ au cours d'un processus isobare ( pression constante). Cela implique que nous pouvons utiliser la relation pour ERROR:8085 avec a capacité thermique à pression constante ($C_p$) et ERROR:7510, exprim e par l' quation :
Cela nous conduit aux valeurs de a température à l'état 3 ($T_3$) et a température à l'état 2 ($T_2$) en utilisant la formule :
Lors du retrait de le chaleur absorbée ($Q_C$), la temp rature du gaz augmente de $T_1$ $T_4$ dans un processus isobare ( pression constante). Cela implique que nous pouvons utiliser la relation pour ERROR:8085 avec a capacité thermique à volume constant ($C_V$) et ERROR:7510, qui est exprim e par l' quation :
Cela nous am ne aux valeurs de a température à l'état 1 ($T_1$) et a température à l'état 4 ($T_4$) en utilisant la formule :
tant donn qu'en cas d'expansion adiabatique, le gaz satisfait aux relations le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$) et le indice adiabatique ($\kappa$), exprim es comme suit :
Nous pouvons noter que lors du changement d' tat de le volume étendu ($V_1$) et a température à l'état 1 ($T_1$) Le volume compressé ($V_2$) et a température à l'état 2 ($T_2$), l' galit suivante est v rifi e :
$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$
En utilisant l' quation pour le entropie molaire de la vapeur ($r_C$) :
Nous obtenons :
tant donn qu'en cas d'expansion adiabatique, le gaz satisfait aux relations le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$), et le indice adiabatique ($\kappa$), exprim es comme suit :
Nous pouvons observer que lors du changement d' tat de le volume intermédiaire ($V_3$) et a température à l'état 3 ($T_3$) Le volume étendu ($V_1$) et a température à l'état 4 ($T_4$), l' galit suivante est v rifi e :
$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$
En utilisant l' quation pour le facteur d'extensibilité ($r_E$) :
Nous obtenons :
Comme le r chauffement se produit pression constante, la loi de Charles s'applique :
Ainsi, le changement d' tat ($V_2, T_2$) ($V_3, T_3$) doit satisfaire l' quation :
$\displaystyle\frac{T_2}{V_2} = \displaystyle\frac{T_3}{V_3}$
Avec les quations :
nous pouvons r crire comme suit :
$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$
c'est- -dire :
La valeur de a efficacité ($\eta$) peut tre calcul e l'aide des valeurs le indice adiabatique ($\kappa$), a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$) dans l' quation suivante :
De plus, les relations entre les temp ratures avec le entropie molaire de la vapeur ($r_C$) et le facteur d'extensibilité ($r_E$) sont d finies par les quations suivantes :
De plus, la valeur de le indice adiabatique ($\kappa$) est utilis e dans l' quation :
Ces quations nous permettent de calculer la performance d'un processus suivant le cycle Diesel l'aide de l' quation suivante :
Lors d'une expansion adiabatique, le gaz respecte la relation impliquant le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) :
Dans ce cas, du point initial 3 au point 4. Cela signifie que pendant l'expansion adiabatique, l' tat du gaz change de le volume compressé ($V_2$) et a température à l'état 3 ($T_3$) Le volume étendu ($V_1$) et a température à l'état 4 ($T_4$) selon :
tant donn qu'en expansion adiabatique, le gaz satisfait la relation avec le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$) et a température à l'état final ($T_f$) :
Dans ce cas, du point initial 1 au point 2. Cela signifie que pendant la compression adiabatique, l' tat du gaz passe de le volume étendu ($V_1$) et a température à l'état 1 ($T_1$) Le volume compressé ($V_2$) et a température à l'état 2 ($T_2$) comme suit :
L'efficacit en fonction de la temp rature est d finie par :
avec les quantit s de chaleur fournies :
et absorb es :
nous avons la relation d'efficacit en fonction de la temp rature :
Exemples
Le cycle Diesel est un cycle thermodynamique qui sous-tend le fonctionnement des moteurs diesel, largement utilis s dans les v hicules et les machines industrielles. D velopp par Rudolf Diesel dans les ann es 1890, ce cycle se distingue principalement de celui d'Otto, utilis dans les moteurs essence, par son processus d'allumage. Dans le cycle Diesel, l'air est aspir dans le cylindre et comprim un taux beaucoup plus lev que dans les moteurs essence, ce qui l ve sa temp rature un niveau suffisant pour enflammer le carburant diesel sans n cessiter de bougie d'allumage.
Lors de son fonctionnement, le cycle commence par l'admission d'air lorsque le piston descend. L'air est ensuite comprim lors de la remont e du piston, augmentant sa temp rature. Au sommet de la phase de compression, du carburant est inject dans l'air comprim et chaud sous forme de fine brume, provoquant une ignition spontan e. La combustion pousse le piston vers le bas, g n rant ainsi de l' nergie. Enfin, lors de la phase d' chappement, les gaz de combustion sont expuls s lorsque le piston remonte, compl tant ainsi le cycle.
Les moteurs Diesel sont reconnus pour leur efficacit et leur durabilit . Le haut taux de compression permet non seulement d'extraire plus d' nergie du carburant, mais augmente galement l'efficience thermique, signifiant qu'une plus grande partie de l' nergie du carburant est convertie en travail m canique. Les moteurs Diesel offrent g n ralement une meilleure efficacit nerg tique et produisent moins d' missions de CO2 par unit d' nergie que leurs homologues essence, mais ils peuvent mettre des niveaux plus lev s d'autres polluants, tels que les oxydes d'azote et les particules.
Sadi Carnot a introduit [1] le concept th orique du premier projet de machine capable de g n rer du travail m canique bas sur un gradient de temp rature. Cela est r alis gr ce un processus dans l'espace pression-volume o la chaleur est ajout e et extraite, comme illustr dans l'image :
La zone sous la courbe le chaleur fournie ($Q_H$), s' tendant de 1 2, repr sente l' nergie n cessaire pour passer de l' tat ($p_1, V_1$) l' tat ($p_2, V_2$). En revanche, la zone sous la courbe le chaleur absorbée ($Q_C$), allant de 2 1, repr sente l'extraction d' nergie n cessaire pour revenir de l' tat ($p_2, V_2$) l' tat ($p_1, V_1$). La diff rence entre ces zones correspond la r gion d limit e par les deux courbes et repr sente le travail efficace ($W$) que le syst me peut accomplir.
Carnot a galement d montr que, conform ment au deuxi me principe de la thermodynamique, le chaleur fournie ($Q_H$) ne peut pas tre nul. Cela implique qu'il n'existe pas de machines capables de convertir toute la chaleur en travail.
[1] "R flexions sur la puissance motrice du feu et sur les machines propres d velopper cette puissance", Sadi Carnot, Annales scientifiques de l .N.S. 2e s rie, tome 1, p. 393-457 (1872)
Rudolf Diesel [1] s'est lanc dans la cr ation d'un cycle diff rent du cycle de Carnot dans le but d'atteindre une meilleure efficacit par rapport au cycle de Otto. Ce processus se d roule en plusieurs tapes :
• tape 1 2 : Compression adiabatique $(p_1,V_1,T_1)\rightarrow (p_2,V_2,T_2)$,
• tape 2 3 : Chauffage et expansion pression constante $(p_2,V_2,T_2)\rightarrow (p_2,V_3,T_3)$,
• tape 3 4 : Expansion adiabatique $(p_2,V_3,T_3)\rightarrow (p_3,V_1,T_4)$,
• tape 4 1 : Refroidissement volume constant $(p_3,V_1,T_4)\rightarrow (p_1,V_1,T_1)$
Ces tapes sont illustr es ci-dessous :
La cl r side dans l' tape 2 3, o l'expansion se produit pression constante. La raison en devient vidente en examinant le graphique :
L' nergie gagn e est gale la surface l'int rieur du cycle, et en effectuant la compression pression constante, cette surface est plus grande que dans le cas de la compression volume constant.
[1] "Verfahren zur Entwickelung eines rationellen W rmemotors zum Ersatz der Dampfmaschine und der heute bekannten Verbrennungsmotoren" (M thode pour le D veloppement d'un Moteur Thermique Rationnel pour Remplacer la Machine Vapeur et les Moteurs Combustion Contemporains), Rudolf Diesel, Kaiserlichen Patentamts, No. 67207 (1892)
Tant le cycle Otto que le cycle Diesel d pendent des variables a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$). Cependant, dans le cas du cycle Diesel, il d pend galement de le indice adiabatique ($\kappa$), dont la valeur est de 1,4.
Dans le cycle Otto, l'efficacit est calcul e en fonction de la temp rature l'aide de l' quation suivante :
Alors que dans le cycle Diesel, l'efficacit est calcul e en fonction de la temp rature l'aide de l' quation suivante :
L'inclusion du facteur $1/\kappa \sim 0,71$ dans le cycle Diesel le rend plus efficace par rapport au cycle Otto pour la m me configuration de temp rature. Cela r sulte directement de l'agrandissement de la zone contenue dans la courbe qui repr sente le cycle dans la repr sentation pression-volume.
tant donn qu'en cas d'expansion adiabatique, le gaz satisfait aux relations le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$), et le indice adiabatique ($\kappa$), exprim es comme suit :
Nous pouvons observer que lors du changement d' tat de le volume intermédiaire ($V_3$) et a température à l'état 3 ($T_3$) Le volume étendu ($V_1$) et a température à l'état 4 ($T_4$), l' galit suivante est v rifi e :
$T_3V_3^{\kappa-1}=T_4V_1^{\kappa-1}$
En utilisant l' quation pour le facteur d'extensibilité ($r_E$) :
Nous obtenons :
tant donn qu'en cas d'expansion adiabatique, le gaz satisfait aux relations le volume à l'état i ($V_i$), le volume à l'état f ($V_f$), a température à l'état initial ($T_i$), a température à l'état final ($T_f$) et le indice adiabatique ($\kappa$), exprim es comme suit :
Nous pouvons noter que lors du changement d' tat de le volume étendu ($V_1$) et a température à l'état 1 ($T_1$) Le volume compressé ($V_2$) et a température à l'état 2 ($T_2$), l' galit suivante est v rifi e :
$T_1V_1^{\kappa-1}=T_2V_2^{\kappa-1}$
En utilisant l' quation pour le entropie molaire de la vapeur ($r_C$) :
Nous obtenons :
Comme le r chauffement se produit pression constante, la loi de Charles s'applique :
Ainsi, le changement d' tat ($V_2, T_2$) ($V_3, T_3$) doit satisfaire l' quation :
$\displaystyle\frac{T_2}{V_2} = \displaystyle\frac{T_3}{V_3}$
Avec les quations :
nous pouvons r crire comme suit :
$T_3 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_2} T_2 = \displaystyle\frac{V_3}{V_1} \displaystyle\frac{V_1}{V_2} T_2 = \displaystyle\frac{r_C}{r_E} T_2$
c'est- -dire :
L'efficacit en fonction de la temp rature est d finie par :
avec les quantit s de chaleur fournies :
et absorb es :
nous avons la relation d'efficacit en fonction de la temp rature :
La valeur de a efficacité ($\eta$) peut tre calcul e l'aide des valeurs le indice adiabatique ($\kappa$), a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et a température à l'état 4 ($T_4$) dans l' quation suivante :
De plus, les relations entre les temp ratures avec le entropie molaire de la vapeur ($r_C$) et le facteur d'extensibilité ($r_E$) sont d finies par les quations suivantes :
De plus, la valeur de le indice adiabatique ($\kappa$) est utilis e dans l' quation :
Ces quations nous permettent de calculer la performance d'un processus suivant le cycle Diesel l'aide de l' quation suivante :
Dans ce cas, du point initial 1 au point 2. Cela signifie que pendant la compression adiabatique, l' tat du gaz passe de le volume étendu ($V_1$) et a température à l'état 1 ($T_1$) Le volume compressé ($V_2$) et a température à l'état 2 ($T_2$) comme suit :
ERROR:8xa0170 peut tre calcul avec a capacité thermique à pression constante ($C_p$), a température à l'état 3 ($T_3$) et a température à l'état 2 ($T_2$) en utilisant la formulexa0:
Dans ce cas, du point initial 3 au point 4. Cela signifie que pendant l'expansion adiabatique, l' tat du gaz change de le volume compressé ($V_2$) et a température à l'état 3 ($T_3$) Le volume étendu ($V_1$) et a température à l'état 4 ($T_4$) selon :
Le chaleur absorbée ($Q_C$) peut tre calcul partir de a capacité thermique à volume constant ($C_V$), a température à l'état 4 ($T_4$) et a température à l'état 1 ($T_1$) l'aide de la formulexa0:
Dans l'analyse du cycle Diesel, il est utile d'introduire ce que l'on appelle le entropie molaire de la vapeur ($r_C$), qui repr sente la relation entre le volume étendu ($V_1$) et le volume compressé ($V_2$) lors de la compression du m lange, comme le montre l'expression suivante :
Dans l'analyse du cycle Diesel, il est avantageux d'introduire le terme le facteur d'extensibilité ($r_E$), qui repr sente la relation entre le volume étendu ($V_1$) et le volume intermédiaire ($V_3$) pendant la compression du m lange, comme illustr dans l'expression suivante :
A température à l'état 3 ($T_3$) peut tre calcul avec a température à l'état 4 ($T_4$), le facteur d'extensibilité ($r_E$) et le indice adiabatique ($\kappa$) en utilisantxa0:
A température à l'état 2 ($T_2$) peut tre calcul partir de a température à l'état 1 ($T_1$), le entropie molaire de la vapeur ($r_C$) et le indice adiabatique ($\kappa$) en utilisantxa0:
A température à l'état 3 ($T_3$) peut tre calcul partir de a température à l'état 2 ($T_2$), le entropie molaire de la vapeur ($r_C$) et le facteur d'extensibilité ($r_E$) en utilisantxa0:
A efficacité ($\eta$) peut tre calcul partir de le indice adiabatique ($\kappa$), a température à l'état 1 ($T_1$), a température à l'état 2 ($T_2$), a température à l'état 3 ($T_3$) et 8492 en utilisantxa0:
Le calcul de a efficacité ($\eta$) est effectu en utilisant le indice adiabatique ($\kappa$), le entropie molaire de la vapeur ($r_C$) et le facteur d'extensibilité ($r_E$), comme suitxa0:
Le chaleur spécifique à pression constante ($c_p$) est gal a capacité thermique à pression constante ($C_p$) divis par a masse ($M$)xa0:
Le chaleur spécifique des gaz à volume constant ($c_V$) est gal a capacité thermique à volume constant ($C_V$) divis par a masse ($M$)xa0:
ID:(1487, 0)